Focus on Fluids
Finger puzzles
-
- Published online by Cambridge University Press:
- 24 January 2012, pp. 1-4
-
- Article
-
- You have access
- Export citation
Papers
Equilibrium transport in double-diffusive convection
-
- Published online by Cambridge University Press:
- 28 September 2011, pp. 5-27
-
- Article
- Export citation
Simulation of a propelled wake with moderate excess momentum in a stratified fluid
-
- Published online by Cambridge University Press:
- 21 December 2011, pp. 28-52
-
- Article
- Export citation
Equilibrium gas–liquid–solid contact angle from density-functional theory
-
- Published online by Cambridge University Press:
- 15 December 2011, pp. 53-77
-
- Article
- Export citation
On the generation of swirling jets: high-Reynolds-number rotating flow in a pipe with a final contraction
-
- Published online by Cambridge University Press:
- 16 December 2011, pp. 78-111
-
- Article
- Export citation
On the cost efficiency of mixing optimization
-
- Published online by Cambridge University Press:
- 16 December 2011, pp. 112-136
-
- Article
- Export citation
Channel turbulence with spanwise rotation studied using helical wave decomposition
-
- Published online by Cambridge University Press:
- 16 December 2011, pp. 137-152
-
- Article
- Export citation
Numerical study of rotational diffusion in sheared semidilute fibre suspension
-
- Published online by Cambridge University Press:
- 21 December 2011, pp. 153-182
-
- Article
- Export citation
Statistical properties of supersonic turbulence in the Lagrangian and Eulerian frameworks
-
- Published online by Cambridge University Press:
- 19 December 2011, pp. 183-206
-
- Article
- Export citation
Effects of acoustic-streaming-induced flow in evaporating nanofluid droplets
-
- Published online by Cambridge University Press:
- 19 December 2011, pp. 207-219
-
- Article
- Export citation
Wavy regime of a power-law film flow
-
- Published online by Cambridge University Press:
- 05 January 2012, pp. 220-256
-
- Article
- Export citation
Trapped modes and Fano resonances in two-dimensional acoustical duct–cavity systems
-
- Published online by Cambridge University Press:
- 05 January 2012, pp. 257-287
-
- Article
- Export citation
Instabilities and turbulence in magnetohydrodynamic flow in a toroidal duct prior to transition in Hartmann layers
-
- Published online by Cambridge University Press:
- 05 January 2012, pp. 288-316
-
- Article
- Export citation
Stressed horizontal convection
-
- Published online by Cambridge University Press:
- 05 January 2012, pp. 317-331
-
- Article
- Export citation
Numerical simulation of flow past a heated/cooled sphere
-
- Published online by Cambridge University Press:
- 05 January 2012, pp. 332-346
-
- Article
- Export citation
Meandering due to large eddies and the statistically self-similar dynamics of quasi-two-dimensional jets
-
- Published online by Cambridge University Press:
- 06 January 2012, pp. 347-368
-
- Article
- Export citation
Rotation of spheroidal particles in Couette flows
-
- Published online by Cambridge University Press:
- 05 January 2012, pp. 369-394
-
- Article
- Export citation
Lagrangian acceleration measurements in convective thermal turbulence
-
- Published online by Cambridge University Press:
- 06 January 2012, pp. 395-419
-
- Article
- Export citation
Asymptotic theory of resonant flow in a spheroidal cavity driven by latitudinal libration
-
- Published online by Cambridge University Press:
- 06 January 2012, pp. 420-445
-
- Article
- Export citation
Granular and fluid washboards
-
- Published online by Cambridge University Press:
- 05 January 2012, pp. 446-463
-
- Article
- Export citation


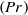 and decreasing with diffusivity ratio
and decreasing with diffusivity ratio 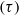 . Theory is successfully tested by a series of direct numerical simulations which span a wide range of
. Theory is successfully tested by a series of direct numerical simulations which span a wide range of 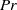 and
and  .
.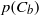 , in the semidilute regime is predicted with this method. The paper emphasizes assessment of the characteristics of a rotary diffusion model – anisotropic in nature (Koch,
, in the semidilute regime is predicted with this method. The paper emphasizes assessment of the characteristics of a rotary diffusion model – anisotropic in nature (Koch, 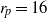 to
to 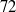 ) and with different volume concentrations (ranging from
) and with different volume concentrations (ranging from 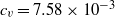 to
to 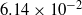 ). A measure of the scalar Folgar–Tucker constant,
). A measure of the scalar Folgar–Tucker constant, 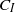 , is extracted from the anisotropic diffusivity tensor,
, is extracted from the anisotropic diffusivity tensor, 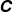 . The scalar
. The scalar 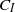 is mostly
is mostly 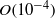 in the semidilute regime and compares very well with the experimental observations of Stover (PhD thesis, School of Chemical Engineering, Cornell University, 1991) and Stover, Koch & Cohen (
in the semidilute regime and compares very well with the experimental observations of Stover (PhD thesis, School of Chemical Engineering, Cornell University, 1991) and Stover, Koch & Cohen (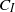 values provide substantial numerical evidence that the range of
values provide substantial numerical evidence that the range of 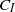 (0.0038–0.0165) obtained by Folgar & Tucker (
(0.0038–0.0165) obtained by Folgar & Tucker (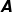 (a second-order orientation tensor). The solution of the evolution equation with the Koch model demonstrates unphysical behaviour at low concentrations. The most plausible explanation for this behaviour is error in the closure approximation; and the use of the Koch model in a spherical harmonics-based method (Montgomery-Smith, Jack & Smith,
(a second-order orientation tensor). The solution of the evolution equation with the Koch model demonstrates unphysical behaviour at low concentrations. The most plausible explanation for this behaviour is error in the closure approximation; and the use of the Koch model in a spherical harmonics-based method (Montgomery-Smith, Jack & Smith, 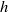 , a local velocity amplitude or the flow rate
, a local velocity amplitude or the flow rate 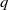 . The models account for the streamwise diffusion of momentum. Comparisons with Orr–Sommerfeld stability analysis and with direct numerical simulation (DNS) show convincing agreement in both linear and nonlinear regimes. The influence of shear-thinning or shear-thickening on the primary instability is shown to be non-trivial. A destabilization of the base flow close to threshold is promoted by the shear-thinning effect, whereas, further from threshold, it tends to stabilize the base flow when the viscous damping of short waves becomes dominant. A reverse situation is observed in the case of shear-thickening fluids. Shear-thinning accelerates solitary waves and promotes a subcritical onset of travelling waves at larger wavenumber than the linear cut-off wavenumber. A conditional stability of the base flow is thus observed. This phenomenon results from a reduction of the effective viscosity at the free surface. When compared with DNS, simulations of the temporal response of the film based on weighted residual models satisfactorily capture the conditional stability of the film.
. The models account for the streamwise diffusion of momentum. Comparisons with Orr–Sommerfeld stability analysis and with direct numerical simulation (DNS) show convincing agreement in both linear and nonlinear regimes. The influence of shear-thinning or shear-thickening on the primary instability is shown to be non-trivial. A destabilization of the base flow close to threshold is promoted by the shear-thinning effect, whereas, further from threshold, it tends to stabilize the base flow when the viscous damping of short waves becomes dominant. A reverse situation is observed in the case of shear-thickening fluids. Shear-thinning accelerates solitary waves and promotes a subcritical onset of travelling waves at larger wavenumber than the linear cut-off wavenumber. A conditional stability of the base flow is thus observed. This phenomenon results from a reduction of the effective viscosity at the free surface. When compared with DNS, simulations of the temporal response of the film based on weighted residual models satisfactorily capture the conditional stability of the film.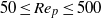 in conditions with and without buoyancy by means of three-dimensional numerical simulation in which temperature dependence of fluid properties such as density and viscosity is exactly taken into account. The results show that in the absence of buoyancy, drag coefficients of the heated and cooled spheres are larger and smaller than those of the adiabatic case, respectively, and their Nusselt numbers are smaller and larger than the values estimated by a widely used empirical expression for predicting Nusselt numbers, respectively. In addition, the temperature difference between the sphere and ambient fluid strongly affects the flow separation points, size of vortex ring behind the sphere and Strouhal number for vortex shedding. These changes are attributed to the temperature dependence of fluid properties in the vicinity of the sphere. Even in the presence of buoyancy, the temperature dependence of fluid properties strongly affects the drag coefficient and Nusselt number and therefore the Boussinesq approximation becomes inapplicable as the temperature difference increases, regardless of the magnitude of the Richardson number.
in conditions with and without buoyancy by means of three-dimensional numerical simulation in which temperature dependence of fluid properties such as density and viscosity is exactly taken into account. The results show that in the absence of buoyancy, drag coefficients of the heated and cooled spheres are larger and smaller than those of the adiabatic case, respectively, and their Nusselt numbers are smaller and larger than the values estimated by a widely used empirical expression for predicting Nusselt numbers, respectively. In addition, the temperature difference between the sphere and ambient fluid strongly affects the flow separation points, size of vortex ring behind the sphere and Strouhal number for vortex shedding. These changes are attributed to the temperature dependence of fluid properties in the vicinity of the sphere. Even in the presence of buoyancy, the temperature dependence of fluid properties strongly affects the drag coefficient and Nusselt number and therefore the Boussinesq approximation becomes inapplicable as the temperature difference increases, regardless of the magnitude of the Richardson number.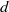 into a fluid confined between two relatively close rigid boundaries with gap
into a fluid confined between two relatively close rigid boundaries with gap 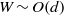 . At large vertical distances
. At large vertical distances 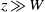 the jet structure consists of a meandering core with large counter-rotating eddies, which develop on alternate sides of the core. Using particle image velocimetry, we observe an inverse cascade typical of quasi-two-dimensional turbulence where both the core and the eddies grow linearly with
the jet structure consists of a meandering core with large counter-rotating eddies, which develop on alternate sides of the core. Using particle image velocimetry, we observe an inverse cascade typical of quasi-two-dimensional turbulence where both the core and the eddies grow linearly with  and travel at an average speed proportional to
and travel at an average speed proportional to 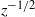 . However, although the present study concerns quasi-two-dimensional confined jets, the jets are self-similar and the mean properties are consistent with both experimental results and theoretical models of the time-averaged properties of fully unconfined planar two-dimensional jets. We believe that the dynamics of the interacting core and large eddies accounts for the Gaussian profile of the mean vertical velocity as shown by the spatial statistical distribution of the core and eddy structure. The lateral excursions (caused by the propagating eddies) of this high-speed central core produce a Gaussian distribution for the time-averaged vertical velocity. In addition, we find that approximately 75 % of the total momentum flux of the jet is contained within the core. The eddies travel substantially slower (at approximately 25 % of the maximum speed of the core) at each height and their growth is primarily attributed to entrainment of ambient fluid. The frequency of occurrence of the eddies decreases in a stepwise manner due to merging, with a well-defined minimum value of the corresponding Strouhal number
. However, although the present study concerns quasi-two-dimensional confined jets, the jets are self-similar and the mean properties are consistent with both experimental results and theoretical models of the time-averaged properties of fully unconfined planar two-dimensional jets. We believe that the dynamics of the interacting core and large eddies accounts for the Gaussian profile of the mean vertical velocity as shown by the spatial statistical distribution of the core and eddy structure. The lateral excursions (caused by the propagating eddies) of this high-speed central core produce a Gaussian distribution for the time-averaged vertical velocity. In addition, we find that approximately 75 % of the total momentum flux of the jet is contained within the core. The eddies travel substantially slower (at approximately 25 % of the maximum speed of the core) at each height and their growth is primarily attributed to entrainment of ambient fluid. The frequency of occurrence of the eddies decreases in a stepwise manner due to merging, with a well-defined minimum value of the corresponding Strouhal number 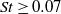 .
.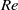 ) exceeding 305. The simulations cover the regime up to
) exceeding 305. The simulations cover the regime up to 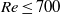 . The rotational behaviour of the spheroid appears to be not only sensitive to the Reynolds number but also to its initial orientation. We discuss the effects of initial orientation in detail. For
. The rotational behaviour of the spheroid appears to be not only sensitive to the Reynolds number but also to its initial orientation. We discuss the effects of initial orientation in detail. For 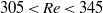 we find that the prolate spheroid reaches a periodic mode characterized by precession and nutation around an inclined axis which is located close to the middle plane where the velocity is zero. For
we find that the prolate spheroid reaches a periodic mode characterized by precession and nutation around an inclined axis which is located close to the middle plane where the velocity is zero. For 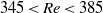 , the prolate spheroid precesses around the vorticity direction with a nutation. For
, the prolate spheroid precesses around the vorticity direction with a nutation. For 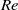 close to the critical
close to the critical 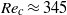 , a period-doubling phenomenon is observed. We also identify a motionless mode at higher Reynolds numbers (
, a period-doubling phenomenon is observed. We also identify a motionless mode at higher Reynolds numbers (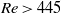 ) for the prolate spheroid. For the oblate spheroid the dynamic equilibrium modes found are log rolling, inclined rolling and different steady states for
) for the prolate spheroid. For the oblate spheroid the dynamic equilibrium modes found are log rolling, inclined rolling and different steady states for 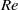 increasing from 0 to 520. The initial-orientation effects are studied by simulations of 57 evenly distributed initial orientations for each
increasing from 0 to 520. The initial-orientation effects are studied by simulations of 57 evenly distributed initial orientations for each 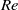 investigated. Only one mode is found for the prolate spheroid for
investigated. Only one mode is found for the prolate spheroid for 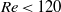 and
and 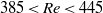 . In other
. In other 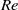 regimes, more than one mode is possible and the final mode is sensitive to the initial orientation. However, the oblate spheroid dynamics are insensitive to its initial orientation.
regimes, more than one mode is possible and the final mode is sensitive to the initial orientation. However, the oblate spheroid dynamics are insensitive to its initial orientation.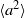 was obtained for various values of the three control parameters: the Rayleigh number
was obtained for various values of the three control parameters: the Rayleigh number 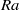 (
(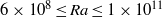 ), the Prandtl number
), the Prandtl number 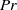 (
(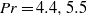 and 6.1) and the system size
and 6.1) and the system size 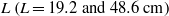 . These were then compared with the theoretically predicted dependence on these parameters for buoyancy-dominated turbulent flows and for homogeneous and isotropic turbulence, respectively. It is found that
. These were then compared with the theoretically predicted dependence on these parameters for buoyancy-dominated turbulent flows and for homogeneous and isotropic turbulence, respectively. It is found that 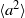 in the central region is dominated by contributions from the turbulent background rather than from the buoyancy force, and the Heisenberg–Yaglom relation holds in this region. From this, we obtain the first experimental results of the constant
in the central region is dominated by contributions from the turbulent background rather than from the buoyancy force, and the Heisenberg–Yaglom relation holds in this region. From this, we obtain the first experimental results of the constant 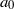 of the acceleration variance in the micro-scale Reynolds number range
of the acceleration variance in the micro-scale Reynolds number range 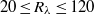 , which fills a gap in this constant in the lower
, which fills a gap in this constant in the lower 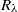 end from the experimental side, and provides possible constraints for its high
end from the experimental side, and provides possible constraints for its high 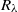 behaviour if a certain fitting function is attempted. In addition, acceleration correlation functions were obtained for different
behaviour if a certain fitting function is attempted. In addition, acceleration correlation functions were obtained for different 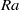 . It is found that the zero crossing time of acceleration correlation functions is at
. It is found that the zero crossing time of acceleration correlation functions is at 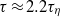 (
(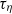 is the Kolmogorov time scale) over the range of
is the Kolmogorov time scale) over the range of 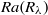 spanned in our experiments, which is the same as the simulation results in isotropic turbulence, and the exponential decay time
spanned in our experiments, which is the same as the simulation results in isotropic turbulence, and the exponential decay time 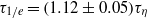 , which is larger than
, which is larger than 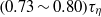 found experimentally for other types of turbulent flows with larger
found experimentally for other types of turbulent flows with larger 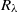 .
. confined within an oblate spheroidal cavity,
confined within an oblate spheroidal cavity, 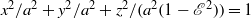 , with eccentricity
, with eccentricity 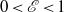 . The spheroidal container rotates rapidly with an angular velocity
. The spheroidal container rotates rapidly with an angular velocity 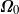 , which is fixed in an inertial frame and defines a small Ekman number
, which is fixed in an inertial frame and defines a small Ekman number 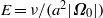 , and undergoes weak latitudinal libration with frequency
, and undergoes weak latitudinal libration with frequency 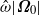 and amplitude
and amplitude 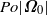 , where
, where 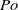 is the Poincaré number quantifying the strength of Poincaré force resulting from latitudinal libration. We investigate, via both asymptotic and numerical analysis, fluid motion in the spheroidal cavity driven by latitudinal libration. When
is the Poincaré number quantifying the strength of Poincaré force resulting from latitudinal libration. We investigate, via both asymptotic and numerical analysis, fluid motion in the spheroidal cavity driven by latitudinal libration. When 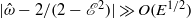 , an asymptotic solution for
, an asymptotic solution for 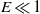 and
and 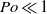 in oblate spheroidal coordinates satisfying the no-slip boundary condition is derived for a spheroidal cavity of arbitrary eccentricity without making any prior assumptions about the spatial–temporal structure of the librating flow. In this case, the librationally driven flow is non-axisymmetric with amplitude
in oblate spheroidal coordinates satisfying the no-slip boundary condition is derived for a spheroidal cavity of arbitrary eccentricity without making any prior assumptions about the spatial–temporal structure of the librating flow. In this case, the librationally driven flow is non-axisymmetric with amplitude 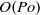 , and the role of the viscous boundary layer is primarily passive such that the flow satisfies the no-slip boundary condition. When
, and the role of the viscous boundary layer is primarily passive such that the flow satisfies the no-slip boundary condition. When 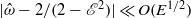 , the librationally driven flow is also non-axisymmetric but latitudinal libration resonates with a spheroidal inertial mode that is in the form of an azimuthally travelling wave in the retrograde direction. The amplitude of the flow becomes
, the librationally driven flow is also non-axisymmetric but latitudinal libration resonates with a spheroidal inertial mode that is in the form of an azimuthally travelling wave in the retrograde direction. The amplitude of the flow becomes 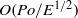 at
at 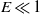 and the role of the viscous boundary layer becomes active in determining the key property of the flow. An asymptotic solution for
and the role of the viscous boundary layer becomes active in determining the key property of the flow. An asymptotic solution for 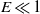 describing the librationally resonant flow is also derived for an oblate spheroidal cavity of arbitrary eccentricity. Three-dimensional direct numerical simulation in an oblate spheroidal cavity is performed to demonstrate that, in both the non-resonant and resonant cases, a satisfactory agreement is achieved between the asymptotic solution and numerical simulation at
describing the librationally resonant flow is also derived for an oblate spheroidal cavity of arbitrary eccentricity. Three-dimensional direct numerical simulation in an oblate spheroidal cavity is performed to demonstrate that, in both the non-resonant and resonant cases, a satisfactory agreement is achieved between the asymptotic solution and numerical simulation at 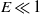 .
.