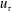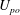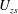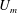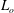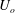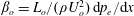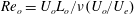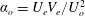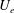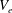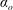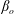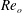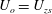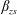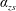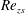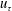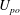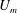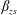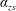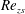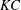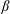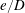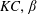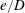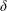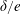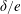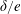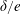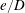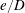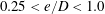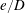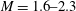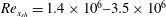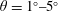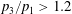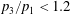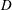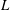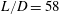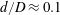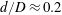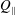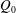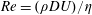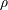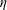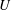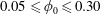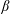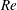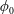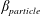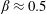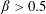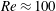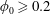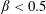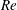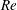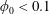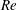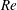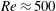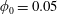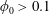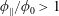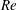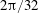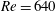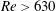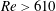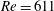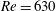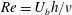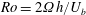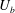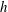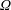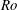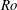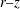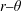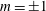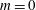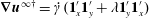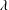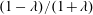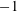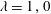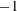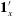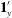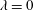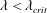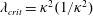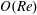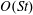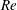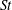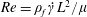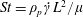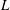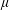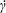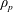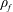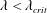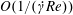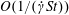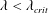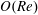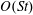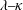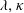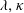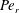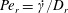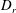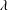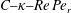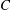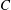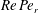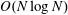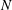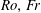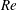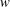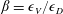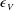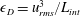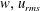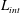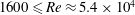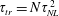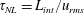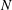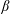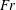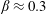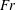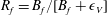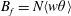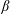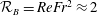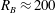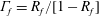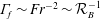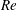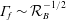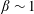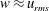The contraction of the heart muscle combines with the opening and closing of the cardiac valves to generate a complex flow in the heart. Predicting this flow presents a significant challenge for computational models, a challenge that Meschini et al. (J. Fluid Mech., vol. 834, 2018, pp. 271–307) tackle head-on by simulating not only the flow in a modelled left ventricle of the heart, but also the coupled dynamics of the mitral valve. The model is validated against a well-designed companion experiment and the authors then proceed to examine the effects of cardiac and valvular dysfunction, as well as prosthetic valves, on ventricular haemodynamics. The insights provided by this study extend from the functional morphology of the left ventricle to the implications of the choice of valve implant on ventricular function.

A clear and consistent framework for the analysis of the outer region of adverse-pressure-gradient turbulent boundary layers is established in this paper based on basic principles and theory, and the help of six adverse-pressure-gradient turbulent boundary layer databases and a zero-pressure-gradient one. Outer velocity and length scales for the mean velocity defect and the Reynolds stresses are discussed first. The conditions of validity of four velocity scales are determined in terms of the shape factor, since one scale is restricted to small velocity-defect boundary layers (the friction velocity $u_{\unicode[STIX]{x1D70F}}$ ), one to large-defect ones (the pressure-gradient velocity $U_{po}$ ), while the two others are proper scales for all velocity-defect conditions (the Zagarola–Smits velocity $U_{zs}$ and the mixing-layer-type velocity $U_{m}$ ). The turbulent boundary layer equations are then used to bring out, in a consistent manner and without assuming any self-similar behaviour, a set of non-dimensional parameters characterizing the outer region of turbulent boundary layers with arbitrary pressure gradients. In terms of a generic outer length scale $L_{o}$ and velocity scale $U_{o}$ , these non-dimensional parameters are the pressure-gradient parameter $\unicode[STIX]{x1D6FD}_{o}=L_{o}/(\unicode[STIX]{x1D70C}U_{o}^{2})\,\text{d}p_{e}/\text{d}x$ , the Reynolds number $Re_{o}=U_{o}L_{o}/\unicode[STIX]{x1D708}(U_{o}/U_{e})$ and the inertial parameter $\unicode[STIX]{x1D6FC}_{o}=U_{e}V_{e}/U_{o}^{2}$ , where $U_{e}$ and $V_{e}$ are respectively the streamwise and wall-normal components of mean velocity at the boundary layer edge. These parameters have a clear physical meaning: they are ratios of the order of magnitude of forces, with the Reynolds shear stress gradient (apparent turbulent force) as the reference force – inertial to apparent turbulent forces for $\unicode[STIX]{x1D6FC}_{o}$ , pressure to apparent turbulent forces for $\unicode[STIX]{x1D6FD}_{o}$ and apparent turbulent to viscous forces for $Re_{o}$ . We discuss at length their significance and determine under what conditions they retain their meaning depending on the outer velocity scale that is considered. The seven boundary layer databases are analysed and compared using the established framework. An astonishing and impressive result is obtained: by choosing $U_{o}=U_{zs}$ , the streamwise evolution of the three ratios of forces in the outer region can be accurately followed with $\unicode[STIX]{x1D6FD}_{zs}$ , $\unicode[STIX]{x1D6FC}_{zs}$ and $Re_{zs}$ in all these flows – not just the order of magnitude of these ratios. This cannot be achieved with $u_{\unicode[STIX]{x1D70F}}$ and $U_{po}$ , and only imperfectly with $U_{m}$ . Consequently, $\unicode[STIX]{x1D6FD}_{zs}$ , $\unicode[STIX]{x1D6FC}_{zs}$ and $Re_{zs}$ can be used to follow – in a global sense – the streamwise evolution of the streamwise mean momentum balance in the outer region.

Application of ring-type plasma actuators for control of laminar–turbulent transition in a swept-wing boundary layer is investigated thorough direct numerical simulations. These actuators induce a wall-normal jet in the boundary layer and can act as virtual roughness elements. The flow configuration resembles experiments by Kim et al. (2016 Technical Report. BUTERFLI Project TR D3.19, http://eprints.nottingham.ac.uk/id/eprint/46529). The actuators are modelled by the volume forces computed from the experimentally measured induced velocity field at the quiescent air condition. Stationary and travelling cross-flow vortices are triggered in the simulations by means of surface roughness and random unsteady perturbations. Interaction of vortices generated by actuators with these perturbations is investigated in detail. It is found that, for successful transition control, the power of the actuators should be increased to generate jet velocities that are one order of magnitude higher than those used in the experiments by Kim et al. (2016) mentioned above.

The coating of discrete objects is an important but poorly understood step in the manufacturing of a broad variety of products. An important model problem is the flow of a thin liquid film on a rotating cylinder, where instabilities can arise and compromise coating uniformity. In this work, we use lubrication theory and flow visualization experiments to study the influence of surfactant on these flows. Two coupled evolution equations describing the variation of film thickness and concentration of insoluble surfactant as a function of time, the angular coordinate and the axial coordinate are solved numerically. The results show that surface-tension forces arising from both axial and angular variations in the angular curvature drive flows in the axial direction that tend to smooth out free-surface perturbations and lead to a stable speed window in which axial perturbations do not grow. The presence of surfactant leads to Marangoni stresses that can cause the stable speed window to disappear by driving flow that opposes the stabilizing flow. In addition, Marangoni stresses tend to reduce the spacing between droplets that form at low rotation rates, and reduce the growth rate of rings that form at high rotation rates. Flow visualization experiments yield observations that are qualitatively consistent with predictions from linear stability analysis and the simulation results. The visualizations also indicate that surfactants tend to suppress dripping, slow the development of free-surface perturbations, and reduce the shifting and merging of rings and droplets, allowing more time for solidifying coatings in practical applications.

Direct numerical simulations of a temporally evolving compressible reacting mixing layer have been performed to study the entrainment of the irrotational flow into the turbulent region across the turbulent/non-turbulent interface (TNTI). In order to study the effects of heat release and interaction of the flame with the TNTI on turbulence several cases with different heat release levels, $Q$ , and stoichiometric mixture fractions are chosen for the simulations with the highest opted value for $Q$ corresponding to hydrogen combustion in air. The combustion is mimicked by a one-step irreversible global reaction, and infinitely fast chemistry approximation is used to compute the species mass fractions. Entrainment is studied via two mechanisms: nibbling, considered as the vorticity transport across the TNTI, and engulfment, the drawing of the pockets of the outside irrotational fluid into the turbulent region. As the level of heat release increases, the total entrained mass flow rate into the mixing layer decreases. In a reacting mixing layer by increasing the heat release rate, the mass flow rate due to nibbling is shown to decrease mostly due to a reduction of the local entrainment velocity, while the surface area of the TNTI does not change significantly. It is also observed that nibbling is a viscous dominated mechanism in non-reacting flows, whereas it is mostly carried out by inviscid terms in reacting flows with high level of heat release. The contribution of the engulfment to entrainment is small for the non-reacting mixing layers, while mass flow rate due to engulfment can constitute close to 40 % of the total entrainment in reacting cases. This increase is primarily related to a decrease of entrained mass flow rate due to nibbling, while the entrained mass flow rate due to engulfment does not change significantly in reacting cases. It is shown that the total entrained mass flow rate in reacting and non-reacting compressible mixing layers can be estimated from an expression containing the convective Mach number and the density change due to heat release.

Oscillatory flow around a circular cylinder close to a plane boundary is numerically investigated at low-to-intermediate Keulegan–Carpenter ( $KC$ ) and Stokes numbers ( $\unicode[STIX]{x1D6FD}$ ) for different gap-to-diameter ratios ( $e/D$ ). A set of unique flow regimes is observed and classified based on the established nomenclature in the ( $KC,\unicode[STIX]{x1D6FD}$ )-space. It is found that the flow is not only influenced by $e/D$ but also by the ratio of the thickness of the Stokes boundary layer ( $\unicode[STIX]{x1D6FF}$ ) to the gap size (e). At relatively large $\unicode[STIX]{x1D6FF}/e$ values, vortex shedding through the gap is suppressed and vortices are only shed from the top of the cylinder. At intermediate values of $\unicode[STIX]{x1D6FF}/e$ , flow through the gap is enhanced, resulting in horizontal gap vortex shedding. As $\unicode[STIX]{x1D6FF}/e$ is further reduced below a critical value, the influence of $\unicode[STIX]{x1D6FF}/e$ becomes negligible and the flow is largely dependent on $e/D$ . A hysteresis phenomenon is observed for the transitions in the flow regime. The physical mechanisms responsible for the hysteresis and the variation of marginal stability curves with $e/D$ are explored at $KC=6$ through specifically designed numerical simulations. The Stokes boundary layer over the plane boundary is found to be responsible for the relatively large hysteresis range over $0.25<e/D<1.0$ . Three mechanisms have been identified to the change of the marginal stability curve over $e/D$ , which are the blockage effect due to the geometry setting, the favourable pressure gradient over the gap and the location of the leading eigenmode relative to the cylinder.

We investigate experimentally the breakup of the Edgerton crown due to Marangoni instability when a highly viscous drop impacts on a thin film of lower-viscosity liquid, which also has different surface tension than the drop liquid. The presence of this low-viscosity film modifies the boundary condition, giving effective slip to the drop along the solid substrate. This allows the high-viscosity drop to form a regular bowl-shaped crown, which rises vertically away from the solid and subsequently breaks up through the formation of a multitude of Marangoni holes. Previous experiments have proposed that the breakup of the crown results from a spray of fine droplets ejected from the thin low-viscosity film on the solid, e.g. Thoroddsen et al. (J. Fluid Mech., vol. 557, 2006, pp. 63–72). These droplets can hit the inner side of the crown forming spots with lower surface tension, which drives a thinning patch leading to the hole formation. We test the validity of this assumption with close-up imaging to identify individual spray droplets, to show how they hit the crown and their lower surface tension drive the hole formation. The experiments indicate that every Marangoni-driven patch/hole is promoted by the impact of such a microdroplet. Surprisingly, in experiments with pools of higher surface tension, we also see hole formation. Here the Marangoni stress changes direction and the hole formation looks qualitatively different, with holes and ruptures forming in a repeatable fashion at the centre of each spray droplet impact. Impacts onto films of the same liquid, or onto an immiscible liquid, do not in general form holes. We furthermore characterize the effects of drop viscosity and substrate-film thickness on the overall evolution of the crown. We also measure the three characteristic velocities associated with the hole formation: i.e. the Marangoni-driven growth of the thinning patches, the rupture speed of the resulting thin films inside these patches and finally the growth rate of the fully formed holes in the crown wall.

High-resolution particle image velocimetry measurements were performed on laminar and transitional oblique shock wave reflections for a range of Mach numbers ( $M=1.6{-}2.3$ ), Reynolds numbers ( $Re_{x_{sh}}=1.4\times 10^{6}{-}3.5\times 10^{6}$ ) and flow deflection angles ( $\unicode[STIX]{x1D703}=1^{\circ }{-}5^{\circ }$ or $p_{3}/p_{1}=1.11{-}1.64$ ). The laminar interactions revealed a long, flat and triangular shaped separation bubble. For relatively strong interactions ( $p_{3}/p_{1}>1.2$ ), the bubble grows linearly in the upstream direction with increasing shock strength. Under these conditions, the boundary layer keeps an on average laminar velocity profile up to the shock impingement location, followed by a quick transition and subsequent reattachment of the boundary layer. For weaker interactions ( $p_{3}/p_{1}<1.2$ ), the boundary layer is able to remain laminar further downstream of the bubble, which consequently results in a later reattachment of the boundary layer. The pressure distribution at the interaction onset for all laminar cases shows excellent agreement with the free-interaction theory, therefore supporting its validity even for incipiently separated laminar oblique shock wave reflections.

We discuss the statistics of acoustic pressure of thermoacoustic oscillations, either axial or azimuthal in nature. We derive a model where the describing functions of the fluctuating heat release rate of the flame and of the acoustic losses appear directly in the equations. The background combustion noise is assumed to be additive, and we show how one can recover, from the measurement of the acoustic pressure at the flame location, the projected describing function of the flame minus the acoustic losses. Using the same equations, one can predict the statistics of the amplitude of acoustic pressure for a certain system. The theory is then tested on an azimuthal thermoacoustic instability in an industrial annular combustor by measuring the state of the system, predicting the acoustic pressure amplitude statistics after a design change and comparing the prediction with the measured statistics after the design change has been implemented.

The flow of a suspension through a bifurcating channel is studied experimentally and by computational methods. The geometry considered is an ‘asymmetric T’, as flow in the entering branch divides to either continue straight or to make a right angle turn. All branches are of the same square cross-section of side length $D$ , with inlet and outlet section lengths $L$ yielding $L/D=58$ in the experiments. The suspensions are composed of neutrally buoyant spherical particles in a Newtonian liquid, with mean particle diameters of $d=250~\unicode[STIX]{x03BC}\text{m}$ and $480~\unicode[STIX]{x03BC}\text{m}$ resulting in $d/D\approx 0.1$ to $d/D\approx 0.2$ for $D=2.4~\text{mm}$ . The flow rate ratio $\unicode[STIX]{x1D6FD}=Q_{\Vert }/Q_{0}$ , defined for the bulk, fluid and particles, is used to characterize the flow behaviour; here $Q_{\Vert }$ and $Q_{0}$ are volumetric flow rates in the straight outlet branch and inlet branch, respectively. The channel Reynolds number $Re=(\unicode[STIX]{x1D70C}DU)/\unicode[STIX]{x1D702}$ was varied over $0<Re<900$ , with $\unicode[STIX]{x1D70C}$ and $\unicode[STIX]{x1D702}$ the fluid density and viscosity, respectively, and $U$ the mean velocity in the inlet channel; the inlet particle volume fraction was $0.05\leqslant \unicode[STIX]{x1D719}_{0}\leqslant 0.30$ . Experimental and numerical results for single-phase Newtonian fluid both show $\unicode[STIX]{x1D6FD}$ increasing with $Re$ , implying more material tending toward the straight branch as the inertia of the flow increases. In suspension flow at small $\unicode[STIX]{x1D719}_{0}$ , inertial migration of particles in the inlet branch affects the flow rate ratio for particles ( $\unicode[STIX]{x1D6FD}_{\mathit{particle}}$ ) and suspension ( $\unicode[STIX]{x1D6FD}_{\mathit{suspension}}$ ). The flow split for the bulk suspension satisfies $\unicode[STIX]{x1D6FD}>0.5$ for $\unicode[STIX]{x1D719}_{0}<0.16$ while $\unicode[STIX]{x1D719}_{0}=0.16$ crosses from $\unicode[STIX]{x1D6FD}\approx 0.5$ to $\unicode[STIX]{x1D6FD}>0.5$ at $Re\approx 100$ . For $\unicode[STIX]{x1D719}_{0}\geqslant 0.2$ , $\unicode[STIX]{x1D6FD}<0.5$ at all $Re$ studied. A complex dependence of the mean solid fraction in the downstream branches upon inlet fraction $\unicode[STIX]{x1D719}_{0}$ and $Re$ is observed: for $\unicode[STIX]{x1D719}_{0}<0.1$ , the solid fraction in the straight downstream branch initially decreases with $Re$ , before increasing to surpass the inlet fraction at large $Re$ ( $Re\approx 500$ for $\unicode[STIX]{x1D719}_{0}=0.05$ ). At $\unicode[STIX]{x1D719}_{0}>0.1$ , the solid fraction in the straight branch satisfies $\unicode[STIX]{x1D719}_{\Vert }/\unicode[STIX]{x1D719}_{0}>1$ , and this ratio grows with $Re$ . Discrete-particle simulations employing immersed boundary and lattice-Boltzmann techniques are used to analyse these phenomena, allowing rationalization of aspects of this complex behaviour as being due to particle migration in the inlet branch.

Direct numerical simulations are carried out to investigate the role of the turbulent region in a self-sustaining system with a spiral vortex structure in the three-dimensional boundary layer over a rotating disk by solving the full Navier–Stokes equations. Two computational domains with two different azimuthal sizes, $2\unicode[STIX]{x03C0}/68$ and $2\unicode[STIX]{x03C0}/32$ , are used to deal with different initially dominant wavenumbers. An artificial disturbance is introduced by short-duration strong suction and blowing on the disk surface. After the flow field reaches a steady state, a turbulent region forms downstream of $Re=640$ . The turbulent region is then removed using two methods: a sponge region, and application of a slip condition at the wall. In both cases, the turbulent region disappears, leaving the spiral vortex structure upstream unaffected. The results suggest that the downstream turbulent region is not related to the velocity fluctuations that grow by the global instability. In addition, when the area where the slip condition is applied is changed from $Re>630$ to $Re>610$ , the velocity fluctuations decay. The results indicate that the vibration source of the velocity fluctuations which grow by the global instability is located between $Re=611$ and $Re=630$ .

Passive scalar transport in turbulent channel flow subject to spanwise system rotation is studied by direct numerical simulations. The Reynolds number $Re=U_{b}h/\unicode[STIX]{x1D708}$ is fixed at 20 000 and the rotation number $Ro=2\unicode[STIX]{x1D6FA}h/U_{b}$ is varied from 0 to 1.2, where $U_{b}$ is the bulk mean velocity, $h$ the half channel gap width and $\unicode[STIX]{x1D6FA}$ the rotation rate. The scalar is constant but different at the two walls, leading to steady scalar transport across the channel. The rotation causes an unstable channel side with relatively strong turbulence and turbulent scalar transport, and a stable channel side with relatively weak turbulence or laminar-like flow, weak turbulent scalar transport but large scalar fluctuations and steep mean scalar gradients. The distinct turbulent–laminar patterns observed at certain $Ro$ on the stable channel side induce similar patterns in the scalar field. The main conclusions of the study are that rotation reduces the similarity between the scalar and velocity field and that the Reynolds analogy for scalar-momentum transport does not hold for rotating turbulent channel flow. This is shown by a reduced correlation between velocity and scalar fluctuations, and a strongly reduced turbulent Prandtl number of less than 0.2 on the unstable channel side away from the wall at higher $Ro$ . On the unstable channel side, scalar scales become larger than turbulence scales according to spectra and the turbulent scalar flux vector becomes more aligned with the mean scalar gradient owing to rotation. Budgets in the governing equations of the scalar energy and scalar fluxes are presented and discussed as well as other statistics relevant for turbulence modelling.

This paper presents 5 kHz stereo particle image velocimetry and OH planar laser induced fluorescence measurements of transversely forced swirl flames. The presence of transverse forcing on this naturally unstable flow both influences the natural instabilities, as well as amplifies disturbances that may not necessarily manifest themselves during natural oscillations. By manipulating the structure of the acoustic forcing field, both axisymmetric and helical modes are preferentially excited away from the frequency of natural instability. The paper presents a method for spatially interpolating the phase locked $r{-}z$ and $r{-}\unicode[STIX]{x1D703}$ planar velocity and flame position data, extracting the full three-dimensional structure of the helical disturbances. These helical disturbances are also decomposed into symmetric and anti-symmetric disturbances about the jet core, showing the subsequent axial evolution (in magnitude and phase) of each of these underlying disturbances. It is shown that out-of-phase acoustic forcing excites $m=\pm 1$ modes, but the flow field preferentially amplifies the counter-winding, co-rotating helical disturbance over the co-winding, counter-rotating helical disturbance. This causes the flow and flame to transition from a transverse flapping near the jet exit to a precessing motion further downstream. In contrast, in-phase forcing promotes axisymmetric $m=0$ disturbances which dominate the flow field over the entire axial domain. In both cases, the amplitudes of the anti-symmetric disturbances about the jet core grow with downstream distance before saturating and decaying, while the symmetric disturbances appear nearly negligible. It is suggested that this saturation and decay is due to linear effects (e.g. a negative spatial growth rate), rather than nonlinear interactions.

In the Stokes limit, the trajectories of neutrally buoyant torque-free non-Brownian spheroids in ambient planar linear flows are well known. These flows form a one-parameter family, with the velocity gradient tensor given by 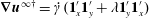$\unicode[STIX]{x1D735}\boldsymbol{u}^{\infty \dagger }=\dot{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{x}^{\prime }\mathbf{1}_{y}^{\prime }+\unicode[STIX]{x1D706}\mathbf{1}_{y}^{\prime }\mathbf{1}_{x}^{\prime })$ . The parameter 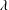$\unicode[STIX]{x1D706}$ is related to the ratio of the vorticity to the extension (given by 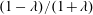$(1-\unicode[STIX]{x1D706})/(1+\unicode[STIX]{x1D706})$ ), and ranges from 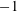$-1$ to 1, with 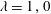$\unicode[STIX]{x1D706}=1\,,0$ and 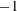$-1$ being planar extensional flow, simple shear flow and solid-body rotation respectively. The unit vectors 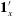$\mathbf{1}_{x}^{\prime }$ and 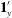$\mathbf{1}_{y}^{\prime }$ are unit vectors along the flow and gradient axes of the simple shear flow ( 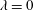$\unicode[STIX]{x1D706}=0$ ). The trajectories, as described by a unit vector along the spheroid symmetry axis, are closed orbits for 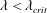$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{crit}$ , where 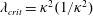$\unicode[STIX]{x1D706}_{crit}=\unicode[STIX]{x1D705}^{2}(1/\unicode[STIX]{x1D705}^{2})$ for an oblate (a prolate) spheroid of aspect ratio $\unicode[STIX]{x1D705}$ . We investigate analytically the orientation dynamics of such a spheroid in the presence of weak inertial effects. The inertial corrections to the angular velocities at 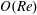$O(Re)$ and 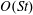$O(St)$ , where 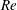$Re$ and 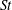$St$ are the Reynolds ( 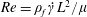$Re=\unicode[STIX]{x1D70C}_{f}\dot{\unicode[STIX]{x1D6FE}}L^{2}/\unicode[STIX]{x1D707}$ ) and Stokes numbers ( 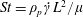$St=\unicode[STIX]{x1D70C}_{p}\dot{\unicode[STIX]{x1D6FE}}L^{2}/\unicode[STIX]{x1D707}$ ) respectively, are derived using a reciprocal theorem formulation. Here, 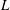$L$ is the semimajor axis of the spheroid, 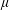$\unicode[STIX]{x1D707}$ is the viscosity of the suspending fluid, 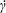$\dot{\unicode[STIX]{x1D6FE}}$ is the shear rate, and 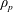$\unicode[STIX]{x1D70C}_{p}$ and 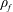$\unicode[STIX]{x1D70C}_{f}$ are the particle and fluid densities respectively. A spheroidal harmonics formalism is then used to evaluate the reciprocal theorem integrals and obtain closed-form expressions for the inertial corrections. The detailed examination of these corrections is restricted to the aforementioned Stokesian closed-orbit regime ( 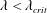$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{crit}$ ). Here, even weak inertia, for asymptotically long times, of 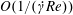$O(1/(\dot{\unicode[STIX]{x1D6FE}}Re))$ or 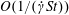$O(1/(\dot{\unicode[STIX]{x1D6FE}}St))$ , will affect the leading-order orientation distribution on account of the indeterminate nature of the distribution across orbits in the Stokes limit. For 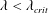$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{crit}$ , inertia results in a drift across the closed orbits in Stokes flow, and this orbital drift is characterized using a multiple time scale analysis. The orbits stabilized by the inertial drift, at 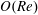$O(Re)$ and 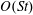$O(St)$ , are identified in the 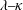$\unicode[STIX]{x1D706}{-}\unicode[STIX]{x1D705}$ plane. For the majority of ( 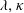$\unicode[STIX]{x1D706},\unicode[STIX]{x1D705}$ ) combinations, the stabilized orbit is either one confined to the plane of symmetry (the flow-gradient plane) of the ambient flow (the tumbling orbit) or one where the spheroid is aligned with the ambient vorticity vector (the spinning orbit). However, for some ( 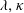$\unicode[STIX]{x1D706},\unicode[STIX]{x1D705}$ ) combinations, depending on the initial orientation, the orbit stabilized can be either the spinning or the tumbling orbit, since both orbits have non-trivial basins of attraction, separated by a pair of unstable (repelling) limit cycles, on the unit sphere of orientations. A stochastic orientation decorrelation mechanism in the form of rotary Brownian motion, characterized by a Péclet number, 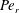$Pe_{r}$ ( 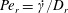$Pe_{r}=\dot{\unicode[STIX]{x1D6FE}}/D_{r}$ , where 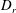$D_{r}$ is the rotary Brownian diffusivity), is included to eliminate the aforementioned dependence on the initial orientation distribution for certain ( 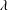$\unicode[STIX]{x1D706}$ , $\unicode[STIX]{x1D705}$ ) combinations. The unique steady-state orientation distribution determined by the combined effect of Brownian motion and inertia is obtained by solving a closed-orbit-averaged drift–diffusion equation. The steady-state orientation dynamics of an inertial spheroid in a planar linear flow, in the presence of weak thermal orientation fluctuations, has similarities to the thermodynamic description of a one-component system. Thus, we identify a tumbling–spinning transition in a 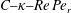$C{-}\unicode[STIX]{x1D705}{-}Re\,Pe_{r}$ space. Here, 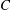$C$ is the orbital coordinate that acts as a label for the closed orbits in the Stokes limit. This transition implies hysteretic orientation dynamics in certain regions in the 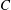$C$ – $\unicode[STIX]{x1D705}$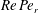 – $Re\,Pe_{r}$ space, although the hysteretic volume shrinks rapidly on either side of simple shear flow. In the hysteretic region, one requires exceedingly large times to achieve the unique steady-state distribution (underlying the thermodynamic interpretation), and for durations relevant to experiments, the system may instead attain an initial-condition-dependent metastable distribution.

Wave-induced roll motions of liquefied natural gas carriers with partially filled spherical tanks are of practical concern. The fluid within the tanks may be excited into resonance and thus strong sloshing motion may occur at certain frequencies. However, the nature of the coupling between internal sloshing and global roll motions, possibly via higher harmonics, is uncertain. A NewWave-type approach, based on the average shape of large waves, is used to examine nonlinearity of the roll response with and without liquid cargo motion. A phase-combination method based on weakly nonlinear theory is adopted to extract the components of the high frequency signals coupled to the low frequency signals. A significant contribution is observed from the higher harmonics of the main roll response, which are coupled to the liquid cargo sloshing motion. This coupling between higher harmonics of the main roll resonance and internal sloshing appears to be linear, despite the internal sloshing being coupled nonlinearly to the low frequency roll.

Hydraulic fracturing is a procedure by which a fracture is initiated and propagates due to pressure (hydraulic loading) applied by a fluid introduced inside the fracture. In this study, we focus on a crack driven by an incompressible Newtonian fluid, injected at a constant rate into an elastic matrix. The injected fluid creates a radial fracture that propagates along a plane. We investigate this type of fracture both theoretically and experimentally. Our experimental apparatus uses a brittle and transparent polyacrylamide hydrogel matrix. Using this medium, we examine the rate of radial crack growth, fracture aperture, shape of the crack tip and internal fluid flow field. Our range of experimental parameters allows us to exhibit two distinct fracturing regimes, and the transition between these, in which the rate of radial crack propagation is dominated by either viscous flow within the fracture or the material toughness. Measurements of the profiles near the crack tip provide additional evidence of the viscosity-dominated and toughness-dominated regimes, and allow us to observe the transition from the viscous to the toughness regime as the crack propagates. Particle image velocimetry measurements show that the flow in the crack is radial, as expected in the viscous regime and in the early stages of the toughness regime. However, at later times in the toughness regime, circulation cells are observed in the flow within the crack that destroy the radial symmetry of the flow field.

We propose a general dynamic reduced-order modelling framework for typical experimental data: time-resolved sensor data and optional non-time-resolved particle image velocimetry (PIV) snapshots. This framework can be decomposed into four building blocks. First, the sensor signals are lifted to a dynamic feature space without false neighbours. Second, we identify a sparse human-interpretable nonlinear dynamical system for the feature state based on the sparse identification of nonlinear dynamics (SINDy). Third, if PIV snapshots are available, a local linear mapping from the feature state to the velocity field is performed to reconstruct the full state of the system. Fourth, a generalized feature-based modal decomposition identifies coherent structures that are most dynamically correlated with the linear and nonlinear interaction terms in the sparse model, adding interpretability. Steps 1 and 2 define a black-box model. Optional steps 3 and 4 lift the black-box dynamics to a grey-box model in terms of the identified coherent structures, if non-time-resolved full-state data are available. This grey-box modelling strategy is successfully applied to the transient and post-transient laminar cylinder wake, and compares favourably with a proper orthogonal decomposition model. We foresee numerous applications of this highly flexible modelling strategy, including estimation, prediction and control. Moreover, the feature space may be based on intrinsic coordinates, which are unaffected by a key challenge of modal expansion: the slow change of low-dimensional coherent structures with changing geometry and varying parameters.

This paper describes an efficient algorithm for computing steady two-dimensional surface gravity waves in irrotational motion. The algorithm complexity is $O(N\log N)$ , $N$ being the number of Fourier modes. This feature allows the arbitrary precision computation of waves in arbitrary depth, i.e. it works efficiently for Stokes, cnoidal and solitary waves, even for quite large steepnesses, up to approximately 99 % of the maximum steepness for all wavelengths. In particular, the possibility to compute very long (cnoidal) waves accurately is a feature not shared by other algorithms and asymptotic expansions. The method is based on conformal mapping, the Babenko equation rewritten in a suitable way, the pseudo-spectral method and Petviashvili iterations. The efficiency of the algorithm is illustrated via some relevant numerical examples. The code is open source, so interested readers can easily check the claims, use and modify the algorithm.

We present a model for the scaling of mixing in weakly rotating stratified flows characterized by their Rossby, Froude and Reynolds numbers $Ro,Fr$ , $Re$ . This model is based on quasi-equipartition between kinetic and potential modes, sub-dominant vertical velocity, $w$ , and lessening of the energy transfer to small scales as measured by a dissipation efficiency $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D716}_{V}/\unicode[STIX]{x1D716}_{D}$ , with $\unicode[STIX]{x1D716}_{V}$ the kinetic energy dissipation and $\unicode[STIX]{x1D716}_{D}=u_{rms}^{3}/L_{int}$ its dimensional expression, with $w,u_{rms}$ the vertical and root mean square velocities, and $L_{int}$ the integral scale. We determine the domains of validity of such laws for a large numerical study of the unforced Boussinesq equations mostly on grids of $1024^{3}$ points, with $Ro/Fr\geqslant 2.5$ , and with $1600\leqslant Re\approx 5.4\times 10^{4}$ ; the Prandtl number is one, initial conditions are either isotropic and at large scale for the velocity and zero for the temperature $\unicode[STIX]{x1D703}$ , or in geostrophic balance. Three regimes in Froude number, as for stratified flows, are observed: dominant waves, eddy–wave interactions and strong turbulence. A wave–turbulence balance for the transfer time $\unicode[STIX]{x1D70F}_{tr}=N\unicode[STIX]{x1D70F}_{NL}^{2}$ , with $\unicode[STIX]{x1D70F}_{NL}=L_{int}/u_{rms}$ the turnover time and $N$ the Brunt–Väisälä frequency, leads to $\unicode[STIX]{x1D6FD}$ growing linearly with $Fr$ in the intermediate regime, with a saturation at $\unicode[STIX]{x1D6FD}\approx 0.3$ or more, depending on initial conditions for larger Froude numbers. The Ellison scale is also found to scale linearly with $Fr$ . The flux Richardson number $R_{f}=B_{f}/[B_{f}+\unicode[STIX]{x1D716}_{V}]$ , with $B_{f}=N\langle w\unicode[STIX]{x1D703}\rangle$ the buoyancy flux, transitions for approximately the same parameter values as for $\unicode[STIX]{x1D6FD}$ . These regimes for the present study are delimited by ${\mathcal{R}}_{B}=ReFr^{2}\approx 2$ and $R_{B}\approx 200$ . With $\unicode[STIX]{x1D6E4}_{f}=R_{f}/[1-R_{f}]$ the mixing efficiency, putting together the three relationships of the model allows for the prediction of the scaling $\unicode[STIX]{x1D6E4}_{f}\sim Fr^{-2}\sim {\mathcal{R}}_{B}^{-1}$ in the low and intermediate regimes for high $Re$ , whereas for higher Froude numbers, $\unicode[STIX]{x1D6E4}_{f}\sim {\mathcal{R}}_{B}^{-1/2}$ , a scaling already found in observations: as turbulence strengthens, $\unicode[STIX]{x1D6FD}\sim 1$ , $w\approx u_{rms}$ , and smaller buoyancy fluxes together correspond to a decoupling of velocity and temperature fluctuations, the latter becoming passive.

Visualisations of various types of flow separation are presented in an experimental set-up that translates a rotating cylinder parallel to a wall. Particle image velocimetry is used to measure the two velocity components in a plane perpendicular to the cylinder where the flow is two-dimensional. To spatially resolve the flow close to the wall, a high-viscosity fluid is used. For a periodic translation, the fixed separation is compared to the theory of Haller (J. Fluid Mech., vol. 512, 2004, pp. 257–311), while for non-periodic translations, a method is proposed to extract the moving separation point captured by a Lagrangian saddle point, and its finite-time unstable direction (separation profiles). Intermediate cases are also presented where both types of separation, fixed and moving, are either present simultaneously or appear successively. Some results issued from numerical simulations of an impinging jet show that all the cases observed in the rotor-oscillator flow are not restricted to high-viscosity fluid motions but may also occur within any vortical flow.