1 Introduction
The mammalian heart has been sculpted by millions of years of evolution into a flow pump par excellence. During the typical lifetime of a human, the heart will beat over three billion times and pump enough blood to fill over 60 Olympic-sized swimming pools. Furthermore, each beat will raise the hydrostatic head of the blood by over 1.5 m, sufficient to overcome the flow resistance of the billions of blood vessels in the body, and provide adequate perfusion to all the tissues of the body.
While it is the heart muscle that powers this astonishing mechanical performance, the movement of blood through the four chambers of the heart is controlled by the cardiac valves. The two-way interaction between the blood flow and the valve leaflets is therefore crucial to the functioning of the heart, and has been the subject of numerous studies (see Yoganathan, He & Jones Reference Yoganathan, He and Jones2004; Sotiropoulos, Le & Gilmanov Reference Sotiropoulos, Le and Gilmanov2016). The first known scientific study of cardiac haemodynamics was carried out by none other than Leonardo da Vinci, who used grass seeds to visualize the flow in glass casts of animal aortas (Robicsek Reference Robicsek1991). In the modern era, a variety of in vivo and in vitro approaches have been used to study intra-cardiac and valvular haemodynamics (Yoganathan et al.
Reference Yoganathan, He and Jones2004), but the limitations inherent to such experiments have left many questions unanswered.
The continuously increasing processing power of computers has opened the door for computational modelling of cardiac haemodynamics, but such modelling is also not without its challenges (Mittal et al.
Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016). Chief among these are the requirement to (i) accurately simulate a highly unsteady, turbulent flow in a geometrically complex, significantly deforming three-dimensional domain, (ii) model fluid–structure interaction between the blood flow and the valve leaflets, and (iii) extract useful insights from the extremely large datasets that emerge from such models. Meschini et al. (Reference Meschini, de Tullio, Querzoli and Verzicco2018, hereafter MTQV) tackle all of these challenges and provide a powerful demonstration of the potential of such models to provide insights that range from fundamental aspects of cardiac function, to practical aspects of surgical interventions.
2 Overview
MTQV focus on the modelling of blood flow through the mitral valve into the left ventricle (LV), which is the primary driver of oxygenated blood to the body. The mitral valve controls the flow between the left atrium and ventricle and is quite prone to dysfunction and replacement. The typical Reynolds number of the flow through the mitral valve is approximately 4000, and this combines with the pumping action to generate a pulsatile turbulent flow in the left ventricle with a wide range of spatial and temporal scales.
Many of the previous computational modelling studies of intra-ventricular flows have focused on singular aspects of the problem such as evaluation of the functional morphology of a specific feature of the ventricle (Pedrizzetti & Domenichini Reference Pedrizzetti and Domenichini2005; Vedula et al.
Reference Vedula, Seo, Lardo and Mittal2016) and/or valves (Seo et al.
Reference Seo, Vijay, Abraham, Lardo, Dawoud, Luo and Mittal2014), or the dynamics of natural and prosthetic valves (Peskin & McQueen Reference Peskin and McQueen1980; Choi, Vedula & Mittal Reference Choi, Vedula and Mittal2014) or validation (Vedula et al.
Reference Vedula, Fortini, Seo, Querzoli and Mittal2014). The focus of MTQV is on the effect of the mitral valve on the haemodynamics of the LV, but a unique aspect of MTQV is that they tackle this problem from multiple fronts.
The natural mitral valve has an extremely complex anatomy, including a non-circular, time-dependent annulus, inhomogeneous tissue properties and chord-like structures (the chordae tendineae) that connect the two leaflets to the walls of the LV (Standring Reference Standring2016). Modelling the fluid–structure interaction of this valve is therefore a significant challenge. MTQV employ a relatively simple model of the natural mitral valve, one that incorporates some key features of its anatomy, but is still realizable in computational models and experiments. The flow is solved using an immersed boundary method (de Tullio & Pascazio Reference de Tullio and Pascazio2016) and the dynamics of the valve leaflets employ an interaction potential approach (Spandan et al.
Reference Spandan, Meschini, Ostilla-Mónico, Lohse, Querzoli, de Tullio and Verzicco2017) that models non-dissipative deformation of membranes with extensional and bending stiffness.
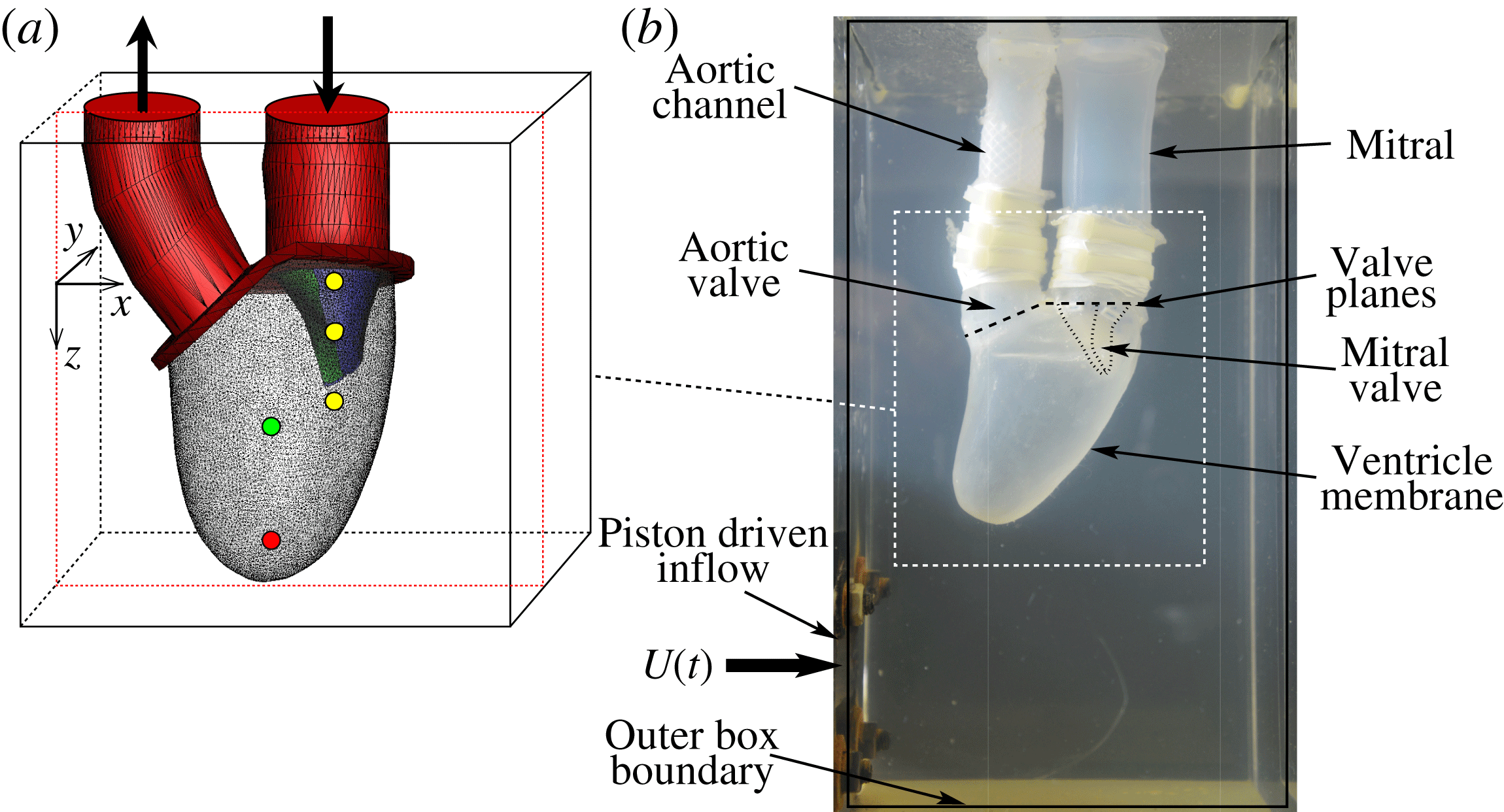
MTQV begin with a validation study where they compare their computed results against a companion experiment that consists of a flexible ventricle with a mitral valve (see figure 1), both made of silicone rubber. The expansion–relaxation of the ventricle in this experiment is driven by a time-varying flow into and out of a sealed Plexiglas tank that surrounds the ventricle. Thus, both the deformation of the ventricle and opening and closing of the mitral valve are a result of fluid–structure interaction, and MTQV show that their model provides a reasonably accurate prediction not only of the movement of the ventricle and the valve leaflets, but also of the flow profiles inside the ventricle.
Following the validation, MTQV establish the characteristics of the flow and valve kinematics for a healthy ventricle (ejection fraction
 $\text{(EF)}=60\,\%$
) with a ‘natural’ healthy mitral valve. The mitral jet is found to generate a circular flow pattern from the lateral to the septal wall of the LV that increases ‘washout’ in the apical region of the LV. MTQV then shift their focus to cases with cardiac pathologies and examine the effect of leaflet stiffness and narrowing (stenosis) of the valve outlet area. They find that the limited mobility of the leaflets leads to a significant increase in jet velocity as well as the pressure drop across the valve. The latter is particularly important from the clinical viewpoint since increased pressure drop can translate into reduced cardiac output and a rise in blood pressure. MTQV also simulate a case with healthy valves but a reduced EF of 40 %, a value that generally signifies borderline mild heart failure (https://my.clevelandclinic.org/health/diseases/17069-heart-failure-understanding-heart-failure/ejection-fraction). The simulations of MTQV indicate that, even with this reduced EF, the washout in the apical region is preserved.
$\text{(EF)}=60\,\%$
) with a ‘natural’ healthy mitral valve. The mitral jet is found to generate a circular flow pattern from the lateral to the septal wall of the LV that increases ‘washout’ in the apical region of the LV. MTQV then shift their focus to cases with cardiac pathologies and examine the effect of leaflet stiffness and narrowing (stenosis) of the valve outlet area. They find that the limited mobility of the leaflets leads to a significant increase in jet velocity as well as the pressure drop across the valve. The latter is particularly important from the clinical viewpoint since increased pressure drop can translate into reduced cardiac output and a rise in blood pressure. MTQV also simulate a case with healthy valves but a reduced EF of 40 %, a value that generally signifies borderline mild heart failure (https://my.clevelandclinic.org/health/diseases/17069-heart-failure-understanding-heart-failure/ejection-fraction). The simulations of MTQV indicate that, even with this reduced EF, the washout in the apical region is preserved.
The subsequent sections of MTQV address the haemodynamics of the LV with two types of valve implants: a bileaflet mechanical valve and a trileaflet bioprosthetic valve. The former is the most commonly used valve prosthesis in the mitral position, and MTQV conduct a number of simulations with this valve and find that it accelerates the breakdown of the mitral jet and consequently diminishes the penetration of the jet into the LV (see figure 2). Simulations with a bioprosthetic valve carried out for two different EFs indicate that the performance of this valve in terms of the LV haemodynamics is noticeably superior to the mechanical valve, although it still cannot beat the natural mitral valve in terms of overall ventricular washout. A more detailed analysis of the haemodynamic performance of the three valves in terms of LV thrombosis risk, effective orifice area (an oft-used metric for characterizing the flow blockage associated with cardiac valves (Yoganathan et al.
Reference Yoganathan, He and Jones2004)), pressure drop across the valves and the ‘global circulation’ generated in the LV consistently shows that the bioprosthetic valve outperforms the mechanical valve but the natural valve exceeds both the others in every computed metric.
Figure 2. Visualization of the flow in the ventricle for the three valves at peak flow rate: natural, bioprosthetic and mechanical with
 $\text{EF}=60\,\%$
. One isosurface of velocity magnitude is shown, coloured with the vertical velocity: range
$\text{EF}=60\,\%$
. One isosurface of velocity magnitude is shown, coloured with the vertical velocity: range
 $-2$
(red) to
$-2$
(red) to
 $+2$
(blue). It is clear that each valve type generates a very distinctive flow pattern and jet penetration. From Meschini et al. (Reference Meschini, de Tullio, Querzoli and Verzicco2018).
$+2$
(blue). It is clear that each valve type generates a very distinctive flow pattern and jet penetration. From Meschini et al. (Reference Meschini, de Tullio, Querzoli and Verzicco2018).
3 Future
The incidence of heart disease is reaching epidemic proportions and, while therapies for heart diseases have generally become more effective over time, the associated cost of treatment has also increased rapidly (Mittal et al.
Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016). Computational modelling such as the type on display in MTQV offers the opportunity to harness the ever-increasing power of computers to deliver cost-efficient improvements in the management of heart disease. Recent inroads made by computational fluid dynamics into clinical cardiology (see Taylor, Fonte & Min Reference Taylor, Fonte and Min2013) only scratch the surface of what is possible. The type of computational modelling represented by the work of MTQV could find use in many aspects of clinical cardiology such as in the diagnosis of heart conditions, design and analysis of cardiac prosthesis, and planning of cardiac surgeries. However, significant advances are still needed before these computational models are ready for deployment in the clinic, and MTQV identify two of these as directions that they are pursuing: adding more realistic anatomical features, and including the physics of activation and contraction of the cardiac muscle.
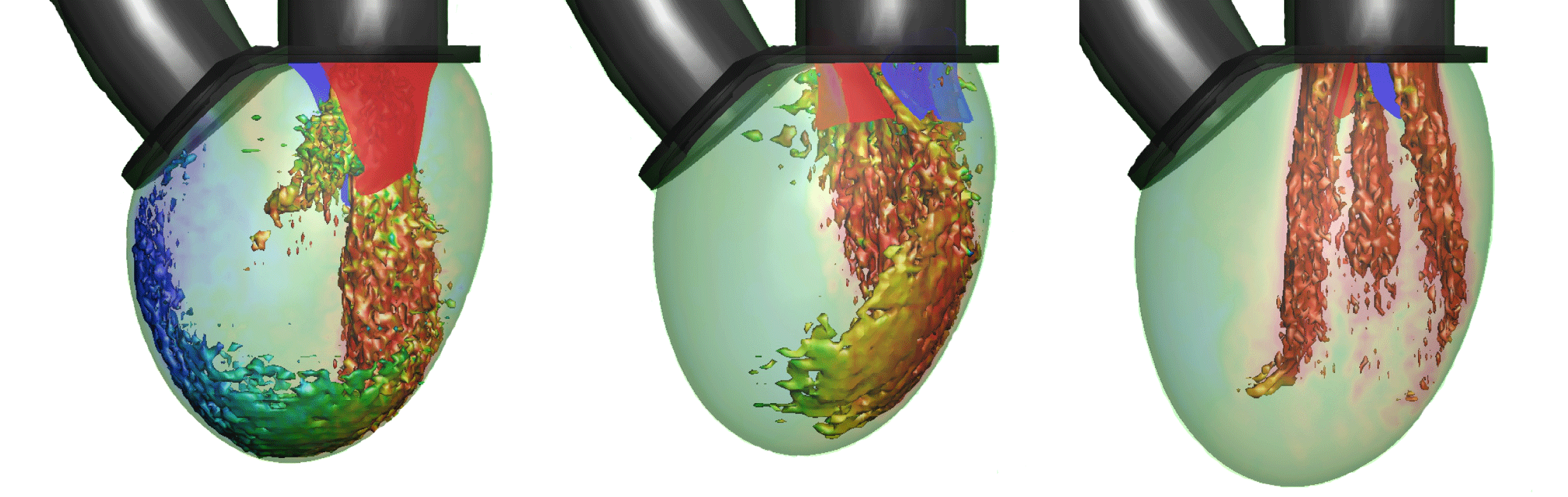
$\text{EF}=60\,\%$. One isosurface of velocity magnitude is shown, coloured with the vertical velocity: range
$-2$ (red) to
$+2$ (blue). It is clear that each valve type generates a very distinctive flow pattern and jet penetration. From Meschini et al. (2018).





1 Introduction
The mammalian heart has been sculpted by millions of years of evolution into a flow pump par excellence. During the typical lifetime of a human, the heart will beat over three billion times and pump enough blood to fill over 60 Olympic-sized swimming pools. Furthermore, each beat will raise the hydrostatic head of the blood by over 1.5 m, sufficient to overcome the flow resistance of the billions of blood vessels in the body, and provide adequate perfusion to all the tissues of the body.
While it is the heart muscle that powers this astonishing mechanical performance, the movement of blood through the four chambers of the heart is controlled by the cardiac valves. The two-way interaction between the blood flow and the valve leaflets is therefore crucial to the functioning of the heart, and has been the subject of numerous studies (see Yoganathan, He & Jones Reference Yoganathan, He and Jones2004; Sotiropoulos, Le & Gilmanov Reference Sotiropoulos, Le and Gilmanov2016). The first known scientific study of cardiac haemodynamics was carried out by none other than Leonardo da Vinci, who used grass seeds to visualize the flow in glass casts of animal aortas (Robicsek Reference Robicsek1991). In the modern era, a variety of in vivo and in vitro approaches have been used to study intra-cardiac and valvular haemodynamics (Yoganathan et al. Reference Yoganathan, He and Jones2004), but the limitations inherent to such experiments have left many questions unanswered.
The continuously increasing processing power of computers has opened the door for computational modelling of cardiac haemodynamics, but such modelling is also not without its challenges (Mittal et al. Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016). Chief among these are the requirement to (i) accurately simulate a highly unsteady, turbulent flow in a geometrically complex, significantly deforming three-dimensional domain, (ii) model fluid–structure interaction between the blood flow and the valve leaflets, and (iii) extract useful insights from the extremely large datasets that emerge from such models. Meschini et al. (Reference Meschini, de Tullio, Querzoli and Verzicco2018, hereafter MTQV) tackle all of these challenges and provide a powerful demonstration of the potential of such models to provide insights that range from fundamental aspects of cardiac function, to practical aspects of surgical interventions.
2 Overview
MTQV focus on the modelling of blood flow through the mitral valve into the left ventricle (LV), which is the primary driver of oxygenated blood to the body. The mitral valve controls the flow between the left atrium and ventricle and is quite prone to dysfunction and replacement. The typical Reynolds number of the flow through the mitral valve is approximately 4000, and this combines with the pumping action to generate a pulsatile turbulent flow in the left ventricle with a wide range of spatial and temporal scales.
Many of the previous computational modelling studies of intra-ventricular flows have focused on singular aspects of the problem such as evaluation of the functional morphology of a specific feature of the ventricle (Pedrizzetti & Domenichini Reference Pedrizzetti and Domenichini2005; Vedula et al. Reference Vedula, Seo, Lardo and Mittal2016) and/or valves (Seo et al. Reference Seo, Vijay, Abraham, Lardo, Dawoud, Luo and Mittal2014), or the dynamics of natural and prosthetic valves (Peskin & McQueen Reference Peskin and McQueen1980; Choi, Vedula & Mittal Reference Choi, Vedula and Mittal2014) or validation (Vedula et al. Reference Vedula, Fortini, Seo, Querzoli and Mittal2014). The focus of MTQV is on the effect of the mitral valve on the haemodynamics of the LV, but a unique aspect of MTQV is that they tackle this problem from multiple fronts.
The natural mitral valve has an extremely complex anatomy, including a non-circular, time-dependent annulus, inhomogeneous tissue properties and chord-like structures (the chordae tendineae) that connect the two leaflets to the walls of the LV (Standring Reference Standring2016). Modelling the fluid–structure interaction of this valve is therefore a significant challenge. MTQV employ a relatively simple model of the natural mitral valve, one that incorporates some key features of its anatomy, but is still realizable in computational models and experiments. The flow is solved using an immersed boundary method (de Tullio & Pascazio Reference de Tullio and Pascazio2016) and the dynamics of the valve leaflets employ an interaction potential approach (Spandan et al. Reference Spandan, Meschini, Ostilla-Mónico, Lohse, Querzoli, de Tullio and Verzicco2017) that models non-dissipative deformation of membranes with extensional and bending stiffness.
Figure 1. (a) Computational model with natural mitral valve leaflets employed in MTQV. (b) Companion experiment used for validation of the computations. From Meschini et al. (Reference Meschini, de Tullio, Querzoli and Verzicco2018).
MTQV begin with a validation study where they compare their computed results against a companion experiment that consists of a flexible ventricle with a mitral valve (see figure 1), both made of silicone rubber. The expansion–relaxation of the ventricle in this experiment is driven by a time-varying flow into and out of a sealed Plexiglas tank that surrounds the ventricle. Thus, both the deformation of the ventricle and opening and closing of the mitral valve are a result of fluid–structure interaction, and MTQV show that their model provides a reasonably accurate prediction not only of the movement of the ventricle and the valve leaflets, but also of the flow profiles inside the ventricle.
Following the validation, MTQV establish the characteristics of the flow and valve kinematics for a healthy ventricle (ejection fraction $\text{(EF)}=60\,\%$
) with a ‘natural’ healthy mitral valve. The mitral jet is found to generate a circular flow pattern from the lateral to the septal wall of the LV that increases ‘washout’ in the apical region of the LV. MTQV then shift their focus to cases with cardiac pathologies and examine the effect of leaflet stiffness and narrowing (stenosis) of the valve outlet area. They find that the limited mobility of the leaflets leads to a significant increase in jet velocity as well as the pressure drop across the valve. The latter is particularly important from the clinical viewpoint since increased pressure drop can translate into reduced cardiac output and a rise in blood pressure. MTQV also simulate a case with healthy valves but a reduced EF of 40 %, a value that generally signifies borderline mild heart failure (https://my.clevelandclinic.org/health/diseases/17069-heart-failure-understanding-heart-failure/ejection-fraction). The simulations of MTQV indicate that, even with this reduced EF, the washout in the apical region is preserved.
$\text{(EF)}=60\,\%$
) with a ‘natural’ healthy mitral valve. The mitral jet is found to generate a circular flow pattern from the lateral to the septal wall of the LV that increases ‘washout’ in the apical region of the LV. MTQV then shift their focus to cases with cardiac pathologies and examine the effect of leaflet stiffness and narrowing (stenosis) of the valve outlet area. They find that the limited mobility of the leaflets leads to a significant increase in jet velocity as well as the pressure drop across the valve. The latter is particularly important from the clinical viewpoint since increased pressure drop can translate into reduced cardiac output and a rise in blood pressure. MTQV also simulate a case with healthy valves but a reduced EF of 40 %, a value that generally signifies borderline mild heart failure (https://my.clevelandclinic.org/health/diseases/17069-heart-failure-understanding-heart-failure/ejection-fraction). The simulations of MTQV indicate that, even with this reduced EF, the washout in the apical region is preserved.
The subsequent sections of MTQV address the haemodynamics of the LV with two types of valve implants: a bileaflet mechanical valve and a trileaflet bioprosthetic valve. The former is the most commonly used valve prosthesis in the mitral position, and MTQV conduct a number of simulations with this valve and find that it accelerates the breakdown of the mitral jet and consequently diminishes the penetration of the jet into the LV (see figure 2). Simulations with a bioprosthetic valve carried out for two different EFs indicate that the performance of this valve in terms of the LV haemodynamics is noticeably superior to the mechanical valve, although it still cannot beat the natural mitral valve in terms of overall ventricular washout. A more detailed analysis of the haemodynamic performance of the three valves in terms of LV thrombosis risk, effective orifice area (an oft-used metric for characterizing the flow blockage associated with cardiac valves (Yoganathan et al. Reference Yoganathan, He and Jones2004)), pressure drop across the valves and the ‘global circulation’ generated in the LV consistently shows that the bioprosthetic valve outperforms the mechanical valve but the natural valve exceeds both the others in every computed metric.
Figure 2. Visualization of the flow in the ventricle for the three valves at peak flow rate: natural, bioprosthetic and mechanical with $\text{EF}=60\,\%$
. One isosurface of velocity magnitude is shown, coloured with the vertical velocity: range
$\text{EF}=60\,\%$
. One isosurface of velocity magnitude is shown, coloured with the vertical velocity: range
 $-2$
(red) to
$-2$
(red) to
 $+2$
(blue). It is clear that each valve type generates a very distinctive flow pattern and jet penetration. From Meschini et al. (Reference Meschini, de Tullio, Querzoli and Verzicco2018).
$+2$
(blue). It is clear that each valve type generates a very distinctive flow pattern and jet penetration. From Meschini et al. (Reference Meschini, de Tullio, Querzoli and Verzicco2018).
3 Future
The incidence of heart disease is reaching epidemic proportions and, while therapies for heart diseases have generally become more effective over time, the associated cost of treatment has also increased rapidly (Mittal et al. Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016). Computational modelling such as the type on display in MTQV offers the opportunity to harness the ever-increasing power of computers to deliver cost-efficient improvements in the management of heart disease. Recent inroads made by computational fluid dynamics into clinical cardiology (see Taylor, Fonte & Min Reference Taylor, Fonte and Min2013) only scratch the surface of what is possible. The type of computational modelling represented by the work of MTQV could find use in many aspects of clinical cardiology such as in the diagnosis of heart conditions, design and analysis of cardiac prosthesis, and planning of cardiac surgeries. However, significant advances are still needed before these computational models are ready for deployment in the clinic, and MTQV identify two of these as directions that they are pursuing: adding more realistic anatomical features, and including the physics of activation and contraction of the cardiac muscle.