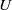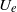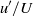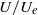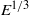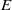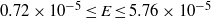Papers
Optimal perturbations of gravitationally unstable, transient boundary layers in porous media
-
- Published online by Cambridge University Press:
- 27 June 2013, pp. 456-487
-
- Article
- Export citation
The response of a continuously stratified fluid to an oscillating flow past an obstacle
-
- Published online by Cambridge University Press:
- 14 June 2013, pp. 83-118
-
- Article
- Export citation
The nonlinear problem of a gliding body with gravity
-
- Published online by Cambridge University Press:
- 14 June 2013, pp. 132-160
-
- Article
- Export citation
Rapids
A note on the mirror-symmetric coherent structure in plane Couette flow
-
- Published online by Cambridge University Press:
- 14 June 2013, R1
-
- Article
- Export citation
Papers
Outer-layer turbulence intensities in smooth- and rough-wall boundary layers
-
- Published online by Cambridge University Press:
- 14 June 2013, pp. 119-131
-
- Article
- Export citation
Boundary-layer noise induced by arrays of roughness elements
-
- Published online by Cambridge University Press:
- 20 June 2013, pp. 282-317
-
- Article
- Export citation
Effects of matrix viscoelasticity on the lateral migration of a deformable drop in a wall-bounded shear
-
- Published online by Cambridge University Press:
- 21 June 2013, pp. 318-345
-
- Article
- Export citation
The structure of sidewall boundary layers in confined rotating Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 27 June 2013, pp. 509-532
-
- Article
- Export citation
An experimental and theoretical investigation of particle–wall impacts in a T-junction
-
- Published online by Cambridge University Press:
- 20 June 2013, pp. 236-255
-
- Article
- Export citation
Drops walking on a vibrating bath: towards a hydrodynamic pilot-wave theory
-
- Published online by Cambridge University Press:
- 28 June 2013, pp. 612-647
-
- Article
- Export citation
Drops bouncing on a vibrating bath
-
- Published online by Cambridge University Press:
- 28 June 2013, pp. 582-611
-
- Article
- Export citation
Stabilization of absolute instability in spanwise wavy two-dimensional wakes
-
- Published online by Cambridge University Press:
- 21 June 2013, pp. 346-378
-
- Article
- Export citation
Depth and minimal slope for surface flows of cohesive granular materials on inclined channels
-
- Published online by Cambridge University Press:
- 19 June 2013, pp. 191-235
-
- Article
- Export citation
A multifold reduction in the transition Reynolds number, and ultra-fast mixing, in a micro-channel due to a dynamical instability induced by a soft wall
-
- Published online by Cambridge University Press:
- 26 June 2013, pp. 407-455
-
- Article
- Export citation
Rapids
On the limitation of imposed velocity field strategy for Coulomb-driven electroconvection flow simulations
-
- Published online by Cambridge University Press:
- 26 June 2013, R3
-
- Article
- Export citation
Papers
Three-dimensional exact coherent states in rotating channel flow
-
- Published online by Cambridge University Press:
- 28 June 2013, pp. 533-581
-
- Article
- Export citation
Thixotropic gravity currents
-
- Published online by Cambridge University Press:
- 14 June 2013, pp. 56-82
-
- Article
- Export citation
Mode C flow transition behind a circular cylinder with a near-wake wire disturbance
-
- Published online by Cambridge University Press:
- 14 June 2013, pp. 30-55
-
- Article
- Export citation
Change in drag, apparent slip and optimum air layer thickness for laminar flow over an idealised superhydrophobic surface
-
- Published online by Cambridge University Press:
- 28 June 2013, pp. 488-508
-
- Article
- Export citation
Locomotion over a viscoplastic film
-
- Published online by Cambridge University Press:
- 14 June 2013, pp. 1-29
-
- Article
- Export citation