This work is devoted to the study of the conditions under which a drop directed normally towards a superheated or isothermal smooth substrate prevents the initial contact with the solid by skating over a micrometre-sized vapour or air layer. The results have been obtained analysing the gas flow at the spatio-temporal region where the maximum liquid pressure is attained, which is also where and when the minimum values of the film thickness are reached. For the common case in which 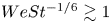 $We St^{-1/6}\gtrsim 1$, where
$We St^{-1/6}\gtrsim 1$, where 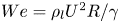 $We=\rho _l U^{2} R/\gamma$ and
$We=\rho _l U^{2} R/\gamma$ and 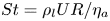 $St=\rho _l U R/\eta _a$ denote, respectively, the Weber and Stokes numbers, we find that capillary effects are negligible and the ratio between the minimum film thickness and the local drop radius of curvature is
$St=\rho _l U R/\eta _a$ denote, respectively, the Weber and Stokes numbers, we find that capillary effects are negligible and the ratio between the minimum film thickness and the local drop radius of curvature is 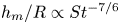 $h_m/R\propto St^{-7/6}$, with
$h_m/R\propto St^{-7/6}$, with 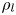 $\rho _l$,
$\rho _l$, 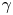 $\gamma$,
$\gamma$, 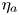 $\eta _a$,
$\eta _a$, 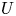 $U$ and
$U$ and 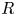 $R$ indicating the liquid density, interfacial tension coefficient, gas viscosity, impact velocity and drop radius, respectively. In contrast, when
$R$ indicating the liquid density, interfacial tension coefficient, gas viscosity, impact velocity and drop radius, respectively. In contrast, when 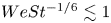 $We St^{-1/6}\lesssim 1$, capillary effects can no longer be neglected and
$We St^{-1/6}\lesssim 1$, capillary effects can no longer be neglected and 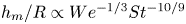 $h_m/R\propto We^{-1/3} St^{-10/9}$. The predicted values of the minimum film thickness are compared with published experimental data, finding good agreement between predictions and measurements for the cases of both isothermal and superheated substrates. In addition, using mass conservation, we have also deduced an equation providing the minimum value of the substrate temperature for which a cylindrical central vapour bubble of constant height
$h_m/R\propto We^{-1/3} St^{-10/9}$. The predicted values of the minimum film thickness are compared with published experimental data, finding good agreement between predictions and measurements for the cases of both isothermal and superheated substrates. In addition, using mass conservation, we have also deduced an equation providing the minimum value of the substrate temperature for which a cylindrical central vapour bubble of constant height 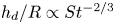 $h_d/R\propto St^{-2/3}$, with
$h_d/R\propto St^{-2/3}$, with 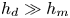 $h_d\gg h_m$, grows radially at the wetting velocity deduced in Riboux & Gordillo (Phys. Rev. Lett., vol. 113, 2014, 024507). The predicted values are in good agreement with the dynamic Leidenfrost temperatures reported by Shirota et al. (Phys. Rev. Lett., vol. 116, 2016, 064501).
$h_d\gg h_m$, grows radially at the wetting velocity deduced in Riboux & Gordillo (Phys. Rev. Lett., vol. 113, 2014, 024507). The predicted values are in good agreement with the dynamic Leidenfrost temperatures reported by Shirota et al. (Phys. Rev. Lett., vol. 116, 2016, 064501).
 $Ta=1500$
$Ta=1500$