Air exchange between people has emerged in the COVID-19 pandemic as the important vector for transmission of the SARS-CoV-2 virus. We study the airflow and exchange between two unmasked individuals conversing face-to-face at short range, which can potentially transfer a high dose of a pathogen, because the dilution is small when compared to long-range airborne transmission. We conduct flow visualization experiments and direct numerical simulations of colliding respiratory jets mimicking the initial phase of a conversation. The evolution and dynamics of the jets are affected by the vertical offset between the mouths of the speakers. At low offsets the head-on collision of jets results in a `blocking effect', temporarily shielding the susceptible speaker from the pathogen carrying jet, although, the lateral spread of the jets is enhanced. Sufficiently large offsets prevent the interaction of the jets. At intermediate offsets (8-10 cm for 1 m separation), jet entrainment and the inhaled breath assist the transport of the pathogen-loaded saliva droplets towards the susceptible speaker's mouth. Air exchange is expected, in spite of the blocking effect arising from the interaction of the respiratory jets from the two speakers.

Using direct numerical simulations performed on periodic cubes of various sizes, the largest being $8192^3$, we examine the nonlinear advection term in the Navier–Stokes equations generating fully developed turbulence. We find significant dissipation even in flow regions where nonlinearity is locally absent. With increasing Reynolds number, the Navier–Stokes dynamics amplifies the nonlinearity in a global sense. This nonlinear amplification with increasing Reynolds number renders the vortex stretching mechanism more intermittent, with the global suppression of nonlinearity, reported previously, restricted to low Reynolds numbers. In regions where vortex stretching is absent, the angle and the ratio between the convective vorticity and solenoidal advection in three-dimensional isotropic turbulence are statistically similar to those in the two-dimensional case, despite the fundamental differences between them.

Just as a solid object would, a liquid jet or a stream of droplets impacting a free surface deforms and perforates it. This generic flow interaction, met in everyday life but also in cutting edge industrial processes, has puzzled scientists for centuries. Lee et al. (J. Fluid Mech., vol. 921, 2021, A8) present an experimental study of a simple droplet train interacting with a liquid bath and identify two stages in the interaction: a first where a cavity elongates and finally bursts, and a second where the interface is steadily punched by the incoming stream. Each of these regimes is explained with elementary but effective models arising from first principles, thereby revealing a full and simple picture of the physics of making holes in liquids.

This paper presents a comprehensive analysis of the momentum and energy transfer in compressible turbulent boundary layers based on integral identities. By considering data obtained from direct numerical simulations for a wide parameter range, the superordinate influences of compressibility, wall heat transfer and pressure gradient on the terms of the governing equations are identified and visualized. This allows us both to determine to what degree cases corresponding to different Mach number, heat transfer and pressure-gradient conditions have physically comparable behaviour and to design turbulent boundary-layer cases with specific sought-after behaviour. To this end, newly formulated identities for the skin-friction coefficient $c_f$ and the specific heat-transfer coefficient $c_h$ from wall-normal integrals based on the non-dimensional compressible momentum and total-enthalpy equations are derived and evaluated. As the individual terms of the resulting identities stay formally close to the terms of the governing equations, the integral analysis further allows the evaluation of common arguments derived from the ‘strong’ Reynolds analogy from an integral perspective. A particular formulation of the Eckert number $Ec$ is proposed as a similarity parameter, mapping cases with different Mach numbers and wall heat transfer conditions.

A series of experiments on stratified Taylor–Couette flow in short aspect ratio wide-gap annuli found an intriguing and not-well-understood dynamics: nonlinear coherent structures appearing and disappearing periodically, along with density layering reminiscent of staircase profiles. A detailed numerical study is presented of the nonlinear dynamics near onset of instability in this setting, which explains most of the characteristics found in the experiments. The simulations show that centrifugal instability of the boundary layer on the inner rotating cylinder produces jets of angular momentum forming Taylor cells that are compressed axially due to the strong stratification. These cells are not axisymmetric from the onset, but are in fact two sets of Taylor cells displaced axially that meet in localized azimuthal defect regions where the cells are patched together; the whole structure is a rotating wave with azimuthal wavenumber $m=1$. The presence of endwalls in this short aspect ratio annulus is critical for the understanding of the dynamics. Their impact cannot be accounted for in idealized axially periodic models. Another key ingredient is the role played by the symmetries of the system. Although the axial reflection symmetry is weakly broken by centrifugal buoyancy effects, following instability there are various branches of solutions corresponding to the different ways the system's symmetries may be broken.

Experimental studies are conducted on a rotationally oscillating cylinder with an attached flexible filament at a Reynolds number of 150. Parametric studies are carried out to investigate the effect of cylinder forcing parameters and filament stiffness on the resultant wake structure. The diagnostics are flow visualization using the laser-induced fluorescence technique, frequency measurement using a hot film, and characterization of the velocity and vorticity field using planar particle image velocimetry. The streamwise force and power are estimated through control volume analysis, using a modified formulation, which considers the streamwise and transverse velocity fluctuations in the wake. These terms become important in a flow field where asymmetric wakes are observed. An attached filament significantly modifies the flow past a rotationally oscillating cylinder from a Bénard–Kármán vortex street to a reverse Bénard–Kármán vortex street, albeit over a certain range of Strouhal number, $St_{A} \sim 0.25\text {--}0.5$, encountered in nature in flapping flight/fish locomotion and in the flow past pitching airfoils. The transition from a Kármán vortex street to a reverse Kármán vortex street precedes the drag-to-thrust transition. The mechanism of unsteady thrust generation is discussed. Maximum thrust is generated at the instants when vortices are shed in the wake from the filament tip. At $St_{A} > 0.4$, a deflected wake associated with the shedding of an asymmetric vortex street is observed. Filament flexibility delays the formation of an asymmetric wake. Wake symmetry is governed by the time instant at which a vortex pair is shed in the wake from the filament tip.

In this paper, we propose a series expansion of the baroclinic torque in low-Mach-number flows, so that the accuracy and universality of any buoyancy term could be examined analytically, and new types of buoyancy terms could be constructed and validated. We first demonstrate that the purpose of introducing a buoyancy term is to approximate the baroclinic torque, and straightforwardly the error of any buoyancy term could be defined with the deviation of its curl from the corresponding baroclinic torque. Then a regular perturbation method is introduced for the elliptic equation of the hydrodynamic pressure in low-Mach-number flows, resulting in a sequence of Poisson equations, whose solutions lead to the series representation of the baroclinic torque and the new types of buoyancy terms. It is found that the frame invariance of the momentum equation is maintained with one of the new types of buoyancy terms. With the error definition of buoyancy terms and the series representation of the baroclinic torque, the validity and accuracy of previous and new buoyancy terms are examined. Finally, numerical simulations confirm that, with a decreasing density variation or an increasing order of our new buoyancy term, the simplified equations can converge to the original low-Mach-number equations.

Turbulent entrainment properties of thermohaline internal hydraulic jumps in quiescent ambient water are investigated. Underflow and overflow jumps are considered. The study is mainly concerned with thermohaline buoyancy effects on flow development. The thermohaline buoyancy is determined from a seawater equation of state, which is nonlinear in temperature and linear in salinity, and is accurate throughout the range of temperature and salinity of interest (T = 0 to 40 °C and S = 0 to 40 ppt). The results indicate that thermohaline buoyancy produces smaller less diluted underflow jumps and larger more diluted overflow jumps. These nonlinear buoyancy effects are particularly significant when buoyancy arising from temperature and salinity act in opposite directions. Hydraulic controls by vertical and/or horizontal constrictions downstream reveal, using a matching technique, unique stationary miscible jump solutions.

High-resolution simulations are performed for gravity currents propagating on a no-slip boundary to study the merging and splitting processes in the lobe-and-cleft structure at a gravity current head. The simulations reproduce the morphological features observed in the laboratory and provide more detailed flow information to elucidate the merging and splitting processes. Our mean lobe width $\tilde {b}$ and mean maximum lobe width $\tilde {b}_{max}$ satisfy the empirical relationships $\tilde {b}/\tilde {d}=7.4 Re^{-0.39}_f$ and $\tilde {b}_{max}/\tilde {d}=12.6 Re^{-0.38}_f$, respectively, over the front Reynolds number in the range $383 \le Re_f \le 3267$, where the front Reynolds number is defined as $Re_f= \tilde {u}_f \tilde {d} / \tilde {\nu }, \tilde {u}_f$ is the front velocity, $\tilde {d}$ is the height of the gravity current head and $\tilde {\nu }$ is the fluid kinematic viscosity. When measured in terms of the viscous length scale $\tilde {\delta }_\nu = \tilde {\nu }/\tilde {u}^*$, where $\tilde {u}^*$ is the shear velocity at the gravity current head, the mean lobe width and the mean maximum lobe width increase with increasing front Reynolds number and asymptotically approach $126 \tilde {\delta }_\nu$ and $230 \tilde {\delta }_\nu$ at $Re_f=3267$, respectively. The vortical structure inside a lobe has an elongated tooth-like shape and a pair of counter-rotating streamwise vortices are positioned on the left- and right-hand sides of each cleft. For the merging process, it requires the interaction of three tooth-like vortices and the middle tooth-like vortex breaks up and reconnects with the two neighbouring tooth-like vortices. Therefore, a cleft may continually merge with another neighbouring cleft but may never disappear. For the splitting process, even before the new cleft appears, a new born streamwise vortex is created by the parent vortex of opposite orientation and the parent vortex can be either the left part or the right part of the existing tooth-like vortex inside the splitting lobe. The new born streamwise vortex then induces the other counter-rotating streamwise vortex as the new cleft develops. The initiation of the splitting process can be attributed to the Brooke–Hanratty mechanism reinforced by the baroclinic production of vorticity. Depending on the orientation of the parent vortex, the resulting new cleft after the splitting process can shift laterally in the positive or negative spanwise direction along the leading edge of the gravity currents as the lobe-and-cleft structure moves forward in the streamwise direction. For gravity currents propagating on a no-slip boundary, the lobe-and-cleft structure is self-sustaining and the manifestations of the merging and splitting processes are in accord with reported laboratory observations.

Inhomogeneous rough surfaces in which strips of roughness alternate with smooth-wall strips are known to generate large-scale secondary motions. Those secondary motions are strongest if the strip width is of the order of the half-channel height and they generate a spatial wall shear stress distribution whose mean value can significantly exceed the area-averaged mean value of a homogeneously smooth and rough surface. In the present paper it is shown that a parametric forcing approach (Busse & Sandham, J. Fluid Mech., vol. 712, 2012, pp. 169–202; Forooghi et al., Intl J. Heat Fluid Flow, vol. 71, 2018, pp. 200–209), calibrated with data from turbulent channel flows over homogeneous roughness, can capture the topological features of the secondary motion over protruding and recessed roughness strips (Stroh et al., J. Fluid Mech., vol. 885, 2020, R5). However, the results suggest that the parametric forcing approach roughness model induces a slightly larger wall offset when applied to the present heterogeneous rough-wall conditions. Contrary to roughness-resolving simulations, where a significantly higher resolution is required to capture roughness geometry, the parametric forcing approach can be applied with usual smooth-wall direct numerical simulation resolution resulting in less computationally expensive simulations for the study of localized roughness effects. Such roughness model simulations are employed to systematically investigate the effect of the relative roughness protrusion on the physical mechanism of secondary flow formation and the related drag increase. It is found that strong secondary motions present over spanwise heterogeneous roughness with geometrical height difference generally lead to a drag increase. However, the physical mechanism guiding the secondary flow formation, and the resulting secondary flow topology, is different for protruding roughness strips and recessed roughness strips separated by protruding smooth surface strips.

We present laboratory measurements of the interaction between thermoelectric currents and turbulent magnetoconvection. In a cylindrical volume of liquid gallium heated from below and cooled from above and subject to a vertical magnetic field, it is found that the large-scale circulation (LSC) can undergo a slow axial precession. Our experiments demonstrate that this LSC precession occurs only when electrically conducting boundary conditions are employed, and that the precession direction reverses when the axial magnetic field direction is flipped. A thermoelectric magnetoconvection (TEMC) model is developed that successfully predicts the zeroth-order magnetoprecession dynamics. Our TEMC magnetoprecession model hinges on thermoelectric current loops at the top and bottom boundaries, which create Lorentz forces that generate horizontal torques on the overturning large-scale circulatory flow. The thermoelectric torques in our model act to drive a precessional motion of the LSC. This model yields precession frequency predictions that are in good agreement with the experimental observations. We postulate that thermoelectric effects in convective flows, long argued to be relevant in liquid metal heat transfer and mixing processes, may also have applications in planetary interior magnetohydrodynamics.

The interaction between small- and large-scale structures and the coexisting bottom-up and top-down processes are studied in a turbulent plane Couette flow, where space-filling longitudinal rolls appear at relatively low values of the Reynolds number $Re$. A direct numerical simulation database at $Re_\tau =101$ is built to replicate the highest $Re$ considered in recent experimental work by Kawata & Alfredsson (Phys. Rev. Lett., vol. 120, 2018, 244501). Our study is based on the exact budget equations for the second-order structure function tensor $\left \langle {\delta u_i \delta u_j} \right \rangle$, i.e. the anisotropic generalized Kolmogorov equations (AGKE). The AGKE study production, redistribution, transport and dissipation of every Reynolds stress tensor component, considering simultaneously the physical space and the space of scales, and properly define the concept of scale in the inhomogeneous wall-normal direction. We show how the large-scale energy-containing motions are involved in the production and redistribution of the turbulent fluctuations. Both bottom-up and top-down interactions occur, and the same is true for direct and inverse cascading. The wall-parallel components $\left \langle {\delta u \delta u} \right \rangle$ and $\left \langle {\delta w \delta w} \right \rangle$ show that both small and large near-wall scales feed the large scales away from the wall. The wall-normal component $\left \langle {\delta v \delta v} \right \rangle$ is different, and shows a dominant top-down dynamics, being produced via pressure-strain redistribution away from the wall and transferred towards near-wall larger scales via an inverse cascade. The off-diagonal component shows a top-down interaction, with both direct and inverse cascades, albeit the latter takes place within a limited range of scales.

We present an analysis of the linear stability characteristics of shock-containing jets. The flow is linearised around a spatially periodic mean, which acts as a surrogate for a mean flow with a shock-cell structure, leading to a set of partial differential equations with periodic coefficients in space. Disturbances are written using the Floquet ansatz and Fourier modes in the streamwise direction, leading to an eigenvalue problem for the Floquet exponent. The characteristics of the solution are directly compared with the locally parallel case, and some of the features are similar. The inclusion of periodicity induces minor changes in the growth rate and phase velocity of the relevant modes for small shock amplitudes. On the other hand, the eigenfunctions are now subject to modulation related to the periodicity of the flow. Analysis of the spatio-temporal growth rates led to the identification of a saddle point between the Kelvin–Helmholtz mode and the guided jet mode, characterising an absolute instability mechanism. Frequencies and mode shapes related to the saddle points for two conditions (associated with axisymmetric and helical modes) are compared with screech frequencies and the most energetic coherent structures of screeching jets, resulting in a good agreement for both. The analysis shows that a periodic shock-cell structure has an impulse response that grows upstream, leading to oscillator behaviour. The results suggest that screech can occur in the absence of a nozzle, and that the upstream reflection condition is not essential for screech frequency selection. Connections to previous models are also discussed.

The role of turbulent large-scale streaks or large-scale motions in forming subaqueous sediment ridges on an initially flat sediment bed is investigated with the aid of particle resolved direct numerical simulations of open channel flow at bulk Reynolds numbers up to 9500. The regular arrangement of quasi-streamwise ridges and troughs at a characteristic spanwise spacing between 1 and 1.5 times the mean fluid height is found to be a consequence of the spanwise organisation of turbulence in large-scale streamwise velocity streaks. Ridges predominantly appear in regions of weaker erosion below large-scale low-speed streaks and vice versa for troughs. The interaction between the dynamics of the large-scale streaks in the bulk flow and the evolution of sediment ridges on the sediment bed is best described as ‘top-down’ process, as the arrangement of the sediment bedforms is seen to adapt to changes in the outer flow with a time delay of several bulk time units. The observed ‘top-down’ interaction between the outer flow and the bed agrees fairly well with the conceptual model on causality in canonical channel flows proposed by Jiménez (J. Fluid Mech., vol. 842, 2018, P1, § 5.6). Mean secondary currents of Prandtl's second kind of comparable intensity and lateral spacing are found over developed sediment ridges and in single-phase smooth-wall channels alike in averages over ${O}(10)$ bulk time units. This indicates that the secondary flow commonly observed together with sediment ridges is the statistical footprint of the regularly organised large-scale streaks.

Large eddy simulation of flow past a circular cylinder of low aspect ratio ($AR=1$ and $3$), spanning subcritical, critical and supercritical regimes, is carried out for $2\times 10^3 \le Re \le 4\times 10^5$. The end walls restrict three-dimensionality of the flow. The critical $Re$ for the onset of the critical regime is significantly lower for small aspect ratio cylinders. The evolution of secondary vortex (SV), laminar separation bubble (LSB) and the related transition of boundary layer with $Re$ is investigated. The plateau in the surface pressure due to LSB is modified by the presence of SV. Proper orthogonal decomposition of surface pressure reveals that although the vortex shedding mode is most dominant throughout the $Re$ regime studied, significant energy of the flow lies in a symmetric mode that corresponds to expansion–contraction of the vortex formation region and is responsible for bursts of weak vortex shedding. A triple decomposition of the time signals comprising of contributions from shear layer vortices, von Kármán vortex shedding and low frequency modulation due to the symmetric mode of flow is proposed. A moving average, with appropriate size of window, is utilized to estimate the component due to vortex shedding. It is used to assess the variation, with $Re$, of strength of vortex shedding as well as its coherence along the span. Weakening of vortex shedding in the high subcritical and critical regime is followed by its rejuvenation in the supercritical regime. Its spanwise correlation is high in the subcritical regime, decreases in the critical regime and improves again in the supercritical regime.

Anelastic convection at high Rayleigh number in a plane parallel layer with no slip boundaries is considered. Energy and entropy balance equations are derived, and they are used to develop scaling laws for the heat transport and the Reynolds number. The appearance of an entropy structure consisting of a well-mixed uniform interior, bounded by thin layers with entropy jumps across them, makes it possible to derive explicit forms for these scaling laws. These are given in terms of the Rayleigh number, the Prandtl number and the bottom to top temperature ratio, which also measures how much the density varies across the layer. The top and bottom boundary layers are examined and they are found to be very different, unlike in the Boussinesq case. Elucidating the structure of these boundary layers plays a crucial part in determining the scaling laws. Physical arguments governing these boundary layers are presented, concentrating on the case in which the boundary layers are so thin that temperature and density vary little across them, even though there may be substantial temperature and density variations across the whole layer. Different scaling laws are found, depending on whether the viscous dissipation is primarily in the boundary layers or in the bulk. The cases of both high and low Prandtl number are considered. Numerical simulations of no-slip anelastic convection up to a Rayleigh number of $10^7$ have been performed and our theoretical predictions are compared with the numerical results.

Flow data are often decomposed using proper orthogonal decomposition (POD) of the space–time separated form, $\boldsymbol {q}'\left (\boldsymbol {x},t\right )=\sum _j a_j\left (t\right )\boldsymbol {\phi }_j\left (\boldsymbol {x}\right )$, which targets spatially correlated flow structures in an optimal manner. This paper analyses permuted POD (PPOD), which decomposes data as $\boldsymbol {q}'\left (\boldsymbol {x},t\right )=\sum _j a_j\left (\boldsymbol {n}\right )\boldsymbol {\phi }_j\left (s,t\right )$, where $\boldsymbol {x}=(s,\boldsymbol {n})$ is a general spatial coordinate system, $s$ is the coordinate along the bulk advection direction and $\boldsymbol {n}=(n_1,n_2)$ are along mutually orthogonal directions normal to the advection characteristic. This separation of variables is associated with a fundamentally different inner product space for which PPOD is optimal and targets correlations in $s,t$ space. This paper presents mathematical features of PPOD, followed by analysis of three experimental datasets from high-Reynolds-number, turbulent shear flows: a wake, a swirling annular jet and a jet in cross-flow. In the wake and swirling jet cases, the leading PPOD and space-only POD modes focus on similar features but differ in convergence rates and fidelity in capturing spatial and temporal information. In contrast, the leading PPOD and space-only POD modes for the jet in cross-flow capture completely different features – advecting shear layer structures and flapping of the jet column, respectively. This example demonstrates how the different inner product spaces, which order the PPOD and space-only POD modes according to different measures of variance, provide unique ‘lenses’ into features of advection-dominated flows, allowing complementary insights.

We model the advective Marangoni spreading of insoluble surfactant at the free surface of a viscous fluid that is confined within a two-dimensional rectangular cavity. Interfacial deflections are assumed small, with contact lines pinned to the walls of the cavity, and inertia is neglected. Linearising the surfactant transport equation about the equilibrium state allows a modal decomposition of the dynamics, with eigenvalues corresponding to decay rates of perturbations. Computation of the family of mutually orthogonal two-dimensional eigenfunctions reveals singular flow structures near each contact line, resulting in spatially oscillatory patterns of shear stress and a pressure field that diverges logarithmically. These singularities at a stationary contact line are associated with dynamic compression of the surfactant monolayer. We show how they can be regularised by weak surface diffusion. Their existence highlights the need for careful treatment in computations of unsteady advection-dominated surfactant transport in confined domains.

Thermally driven flows in fractures play a key role in enhancing the heat transfer and fluid mixing across the Earth's lithosphere. Yet the energy pathways in such confined environments have not been characterised. Building on Letelier et al. (J. Fluid Mech., vol. 864, 2019, pp. 746–767), we introduce novel expressions for energy transfer rates – energetics – of geometrically constrained Rayleigh–Bénard convection in Hele-Shaw cells (HS-RBC) based on two different conceptual frameworks. First, we derived the energetics following the well-established framework introduced by Winters et al. (J. Fluid Mech., vol. 289, 1995, pp. 115–128), in which the gravitational potential energy, 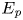$E_{\textit {p}}$, is decomposed into its available, 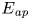$E_{\textit {ap}}$, and background, 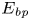$E_{\textit {bp}}$, components. Secondly, we derived the energetics considering a new decomposition for 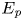$E_{\textit {p}}$, named dynamic, 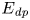$E_{\textit {dp}}$, and reference, 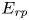$E_{\textit {rp}}$, potential energies; 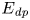$E_{\textit {dp}}$ is defined as the departure of the system's potential energy from the reference state 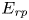$E_{\textit {rp}}$, determined by the ‘energy’ of the scalar fluctuations. For HS-RBC, both frameworks lead to the same energy transfer rates at a steady state, satisfying the relationship 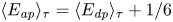$\langle E_{\textit {ap}} \rangle _{\tau } = \langle E_{\textit {dp}} \rangle _{\tau } + 1/6$. Consistent with the work by Hughes et al. (J. Fluid Mech., vol. 729, 2013) on three-dimensional Rayleigh–Bénard convection, we report analytical expressions for the energetics and efficiencies of HS-RBC in terms of the Rayleigh number and the global Nusselt number. Additionally, we performed numerical experiments to illustrate the application of the energetics for the analysis of HS-RBC. Finally, we discuss the impact of the thermal forcing and the geometrical control exerted by Hele-Shaw cells on the development of boundary layers, protoplumes and the self-organisation of large-scale flows.

We study the properties of homogeneous and isotropic turbulence in higher spatial dimensions through the lens of chaos and predictability using numerical simulations. We employ both direct numerical simulations and numerical calculations of the eddy damped quasi-normal Markovian closure approximation. Our closure results show a remarkable transition to a non-chaotic regime above the critical dimension, $d_c$, which is found to be approximately 5.88. We relate these results to the properties of the energy cascade as a function of spatial dimension in the context of the idea of a critical dimension for turbulence where Kolmogorov's 1941 theory becomes exact.