Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-22T01:44:53.012Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical transition to a non-chaotic regime in isotropic turbulence

Published online by Cambridge University Press:  10 November 2021

Daniel Clark Open the ORCID record for Daniel Clark [Opens in a new window] ,
Andres Armua Open the ORCID record for Andres Armua [Opens in a new window] ,
Richard D.J.G. Ho Open the ORCID record for Richard D.J.G. Ho [Opens in a new window]  and
Arjun Berera Open the ORCID record for Arjun Berera [Opens in a new window]
Daniel Clark*
Affiliation:
SUPA, School of Physics and Astronomy, University of Edinburgh, JCMB, King's Buildings, Peter Guthrie Tait Road, EdinburghEH9 3FD, UK
Andres Armua
Affiliation:
SUPA, School of Physics and Astronomy, University of Edinburgh, JCMB, King's Buildings, Peter Guthrie Tait Road, EdinburghEH9 3FD, UK
Richard D.J.G. Ho
Affiliation:
Institute of Theoretical Physics, Jagiellonian University, Łojasiewicza 11, 30-348Kraków, Poland
Arjun Berera
Affiliation:
SUPA, School of Physics and Astronomy, University of Edinburgh, JCMB, King's Buildings, Peter Guthrie Tait Road, EdinburghEH9 3FD, UK
*
†Email address for correspondence: daniel-clark@ed.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

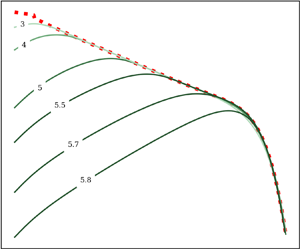
We study the properties of homogeneous and isotropic turbulence in higher spatial dimensions through the lens of chaos and predictability using numerical simulations. We employ both direct numerical simulations and numerical calculations of the eddy damped quasi-normal Markovian closure approximation. Our closure results show a remarkable transition to a non-chaotic regime above the critical dimension, $d_c$, which is found to be approximately 5.88. We relate these results to the properties of the energy cascade as a function of spatial dimension in the context of the idea of a critical dimension for turbulence where Kolmogorov's 1941 theory becomes exact.

JFM classification

Nonlinear Dynamical Systems: Chaos Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 930 , 10 January 2022 , A17
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aji, V. & Goldenfeld, N. 2001 Fluctuations in finite critical and turbulent systems. Phys. Rev. Lett. 86 (6), 1007.10.1103/PhysRevLett.86.1007CrossRefGoogle ScholarPubMed
Anselmet, F., Gagne, Y., Hopfinger, E.J. & Antonia, R.A. 1984 High-order velocity structure functions in turbulent shear flows. J. Fluid Mech. 140, 63–89.10.1017/S0022112084000513CrossRefGoogle Scholar
Antonia, R.A., Djenidi, L., Danaila, L. & Tang, S.L. 2017 Small scale turbulence and the finite Reynolds number effect. Phys. Fluids 29 (2), 020715.10.1063/1.4974323CrossRefGoogle Scholar
Antonia, R.A., Tang, S.L., Djenidi, L. & Zhou, Y. 2019 Finite Reynolds number effect and the 4/5 law. Phys. Rev. Fluids 4 (8), 084602.10.1103/PhysRevFluids.4.084602CrossRefGoogle Scholar
Baerenzung, J., Politano, H., Ponty, Y. & Pouquet, A. 2008 Spectral modeling of magnetohydrodynamic turbulent flows. Phys. Rev. E 78 (2), 026310.10.1103/PhysRevE.78.026310CrossRefGoogle ScholarPubMed
Batchelor, G.K. 1969 Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids 12 (12), II–233.10.1063/1.1692443CrossRefGoogle Scholar
Bell, T.L. & Nelkin, M. 1978 Time-dependent scaling relations and a cascade model of turbulence. J. Fluid Mech. 88 (2), 369–391.10.1017/S0022112078002165CrossRefGoogle Scholar
Benavides, S.J. & Alexakis, A. 2017 Critical transitions in thin layer turbulence. J. Fluid Mech. 822, 364–385.10.1017/jfm.2017.293CrossRefGoogle Scholar
Berera, A. & Ho, R.D.J.G. 2018 Chaotic properties of a turbulent isotropic fluid. Phys. Rev. Lett. 120, 024101.10.1103/PhysRevLett.120.024101CrossRefGoogle ScholarPubMed
Berera, A., Ho, R.D.J.G. & Clark, D. 2020 Homogeneous isotropic turbulence in four spatial dimensions. Phys. Fluids 32 (8), 085107.10.1063/5.0022929CrossRefGoogle Scholar
Boffetta, G., Celani, A., Crisanti, A. & Vulpiani, A. 1997 Predictability in two-dimensional decaying turbulence. Phys. Fluids 9 (3), 724–734.10.1063/1.869227CrossRefGoogle Scholar
Boffetta, G. & Musacchio, S. 2001 Predictability of the inverse energy cascade in 2D turbulence. Phys. Fluids 13 (4), 1060–1062.10.1063/1.1350877CrossRefGoogle Scholar
Boffetta, G. & Musacchio, S. 2017 Chaos and predictability of homogeneous-isotropic turbulence. Phys. Rev. Lett. 119, 054102.10.1103/PhysRevLett.119.054102CrossRefGoogle ScholarPubMed
Bos, W.J.T. 2021 Three-dimensional turbulence without vortex stretching. J. Fluid Mech. 915, A121.10.1017/jfm.2021.194CrossRefGoogle Scholar
Bos, W.J.T., Chevillard, L., Scott, J.F. & Rubinstein, R. 2012 Reynolds number effect on the velocity increment skewness in isotropic turbulence. Phys. Fluids 24 (1), 015108.10.1063/1.3678338CrossRefGoogle Scholar
Bowman, J.C. 1996 On inertial-range scaling laws. J. Fluid Mech. 306, 167–181.10.1017/S0022112096001279CrossRefGoogle Scholar
Bramwell, S.T., Holdsworth, P.C.W. & Pinton, J.-F. 1998 Universality of rare fluctuations in turbulence and critical phenomena. Nature 396 (6711), 552–554.10.1038/25083CrossRefGoogle Scholar
Buaria, D., Bodenschatz, E. & Pumir, A. 2020 Vortex stretching and enstrophy production in high Reynolds number turbulence. Phys. Rev. Fluids 5 (10), 104602.10.1103/PhysRevFluids.5.104602CrossRefGoogle Scholar
Carbone, M. & Bragg, A.D. 2020 Is vortex stretching the main cause of the turbulent energy cascade? J. Fluid Mech. 883, R2.10.1017/jfm.2019.923CrossRefGoogle Scholar
Celani, A., Rubenthaler, S. & Vincenzi, D. 2010 Dispersion and collapse in stochastic velocity fields on a cylinder. J. Stat. Phys. 138 (4–5), 579–597.10.1007/s10955-009-9875-1CrossRefGoogle Scholar
Clark, D., Armua, A., Freeman, C., Brener, D.J. & Berera, A. 2021 a Chaotic measure of the transition between two and three dimensional turbulence. Phys. Rev. Fluids 6 (5), 054612.10.1103/PhysRevFluids.6.054612CrossRefGoogle Scholar
Clark, D., Ho, R.D.J.G. & Berera, A. 2021 b Effect of spatial dimension on a model of fluid turbulence. J. Fluid Mech. 912, A40.10.1017/jfm.2020.1173CrossRefGoogle Scholar
Clark, D., Tarra, L. & Berera, A. 2020 Chaos and information in two-dimensional turbulence. Phys. Rev. Fluids 5 (6), 064608.10.1103/PhysRevFluids.5.064608CrossRefGoogle Scholar
Cole, J.D. 1951 On a quasi-linear parabolic equation occurring in aerodynamics. Q. Appl. Maths 9 (3), 225–236.10.1090/qam/42889CrossRefGoogle Scholar
De Gennes, P.G. 1975 Phase transition and turbulence: an introduction. In Fluctuations, Instabilities, and Phase Transitions (ed. T. Riste), pp. 1–18. Springer.10.1007/978-1-4615-8912-9_1CrossRefGoogle Scholar
DeDominicis, C. & Martin, P.C. 1979 Energy spectra of certain randomly-stirred fluids. Phys. Rev. A 19 (1), 419.10.1103/PhysRevA.19.419CrossRefGoogle Scholar
Deissler, R.G. 1986 Is Navier–Stokes turbulence chaotic? Phys. Fluids 29 (5), 1453–1457.10.1063/1.865663CrossRefGoogle Scholar
Djenidi, L., Antonia, R.A. & Tang, S.L. 2019 Scale invariance in finite Reynolds number homogeneous isotropic turbulence. J. Fluid Mech. 864, 244–272.10.1017/jfm.2019.28CrossRefGoogle Scholar
Falkovich, G. 1994 Bottleneck phenomenon in developed turbulence. Phys. Fluids 6 (4), 1411–1414.10.1063/1.868255CrossRefGoogle Scholar
Falkovich, G., Fouxon, I. & Oz, Y. 2010 New relations for correlation functions in Navier–Stokes turbulence. J. Fluid Mech. 644, 465–472.10.1017/S0022112009993429CrossRefGoogle Scholar
Forster, D., Nelson, D.R. & Stephen, M.J. 1976 Long-time tails and the large-eddy behavior of a randomly stirred fluid. Phys. Rev. Lett. 36 (15), 867.10.1103/PhysRevLett.36.867CrossRefGoogle Scholar
Forster, D., Nelson, D.R. & Stephen, M.J. 1977 Large-distance and long-time properties of a randomly stirred fluid. Phys. Rev. A 16 (2), 732.10.1103/PhysRevA.16.732CrossRefGoogle Scholar
Fournier, J.-D. & Frisch, U. 1978 $d$-dimensional turbulence. Phys. Rev. A 17 (2), 747.10.1103/PhysRevA.17.747CrossRefGoogle Scholar
Fournier, J.-D., Frisch, U. & Rose, H.A. 1978 Infinite-dimensional turbulence. J. Phys. A: Math. Gen. 11 (1), 187.10.1088/0305-4470/11/1/020CrossRefGoogle Scholar
Frisch, U., Lesieur, M. & Sulem, P.L. 1976 Crossover dimensions for fully developed turbulence. Phys. Rev. Lett. 37 (14), 895.10.1103/PhysRevLett.37.895CrossRefGoogle Scholar
Frisch, U. & Parisi, G. 1980 Fully developed turbulence and intermittency. Ann. NY Acad. Sci. 357, 359–367.10.1111/j.1749-6632.1980.tb29703.xCrossRefGoogle Scholar
Frisch, U., Pomyalov, A., Procaccia, I. & Ray, S.S. 2012 Turbulence in noninteger dimensions by fractal Fourier decimation. Phys. Rev. Lett. 108 (7), 074501.10.1103/PhysRevLett.108.074501CrossRefGoogle ScholarPubMed
Frisch, U., Sulem, P.-L. & Nelkin, M. 1978 A simple dynamical model of intermittent fully developed turbulence. J. Fluid Mech. 87 (4), 719–736.10.1017/S0022112078001846CrossRefGoogle Scholar
Gat, O., Procaccia, I. & Zeitak, R. 1998 Anomalous scaling in passive scalar advection: Monte Carlo Lagrangian trajectories. Phys. Rev. Lett. 80 (25), 5536.10.1103/PhysRevLett.80.5536CrossRefGoogle Scholar
Gawedzki, K. & Vergassola, M. 2000 Phase transition in the passive scalar advection. Physica D 138 (1–2), 63–90.10.1016/S0167-2789(99)00171-2CrossRefGoogle Scholar
Ginzburg, V.L. 1960 Some remarks on second order phase transitions and microscopic theory of ferroelectrics. Fiz. Tverd. Tela 2 (9), 2031–2034.Google Scholar
Giuliani, P., Jensen, M.H. & Yakhot, V. 2002 Critical ‘dimension’ in shell model turbulence. Phys. Rev. E 65 (3), 036305.10.1103/PhysRevE.65.036305CrossRefGoogle ScholarPubMed
Gotoh, T., Watanabe, Y., Shiga, Y., Nakano, T. & Suzuki, E. 2007 Statistical properties of four-dimensional turbulence. Phys. Rev. E 75 (1), 016310.10.1103/PhysRevE.75.016310CrossRefGoogle ScholarPubMed
Ho, R.D.J.G. 2019 Effects of macroscopic variables on turbulent evolution. PhD thesis, University of Edinburgh.Google Scholar
Ho, R.D.J.G., Armua, A. & Berera, A. 2020 Fluctuations of Lyapunov exponents in homogeneous and isotropic turbulence. Phys. Rev. Fluids 5 (2), 024602.10.1103/PhysRevFluids.5.024602CrossRefGoogle Scholar
Ho, R.D.J.G., Berera, A. & Clark, D. 2019 Chaotic behavior of Eulerian magnetohydrodynamic turbulence. Phys. Plasmas 26 (4), 042303.10.1063/1.5092367CrossRefGoogle Scholar
Hopf, E. 1950 The partial differential equation $u_t+ uu_x= \mu _{xx}$. Commun. Pure Appl. Maths 3 (3), 201–230.10.1002/cpa.3160030302CrossRefGoogle Scholar
Ishihara, T., Kaneda, Y., Morishita, K., Yokokawa, M. & Uno, A. 2020 Second-order velocity structure functions in direct numerical simulations of turbulence with $\textrm {R}_{\lambda }$ up to 2250. Phys. Rev. Fluids 5 (10), 104608.10.1103/PhysRevFluids.5.104608CrossRefGoogle Scholar
Iyer, K.P., Sreenivasan, K.R. & Yeung, P.K. 2019 Circulation in high Reynolds number isotropic turbulence is a bifractal. Phys. Rev. X 9 (4), 041006.Google Scholar
Iyer, K.P., Sreenivasan, K.R. & Yeung, P.K. 2020 Scaling exponents saturate in three-dimensional isotropic turbulence. Phys. Rev. Fluids 5 (5), 054605.10.1103/PhysRevFluids.5.054605CrossRefGoogle Scholar
Johnson, P.L. 2020 Energy transfer from large to small scales in turbulence by multiscale nonlinear strain and vorticity interactions. Phys. Rev. Lett. 124 (10), 104501.10.1103/PhysRevLett.124.104501CrossRefGoogle ScholarPubMed
Kolmogorov, A.N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. C. R. Acad. Sci. URSS 30, 301–305.Google Scholar
Kolmogorov, A.N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13 (1), 82–85.10.1017/S0022112062000518CrossRefGoogle Scholar
Kraichnan, R.H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10 (7), 1417–1423.10.1063/1.1762301CrossRefGoogle Scholar
Kraichnan, R.H. 1974 a Convection of a passive scalar by a quasi-uniform random straining field. J. Fluid Mech. 64 (4), 737–762.10.1017/S0022112074001881CrossRefGoogle Scholar
Kraichnan, R.H. 1974 b On Kolmogorov's inertial-range theories. J. Fluid Mech. 62 (2), 305–330.10.1017/S002211207400070XCrossRefGoogle Scholar
Kraichnan, R.H. 1991 Turbulent cascade and intermittency growth. Proc. R. Soc. Lond. A 434 (1890), 65–78.Google Scholar
Landau, L.D. & Lifshitz, E.M. 1959 Fluid Mechanics. Pergamon.Google Scholar
Lanotte, A.S., Benzi, R., Malapaka, S.K., Toschi, F. & Biferale, L. 2015 Turbulence on a fractal Fourier set. Phys. Rev. Lett. 115 (26), 264502.10.1103/PhysRevLett.115.264502CrossRefGoogle ScholarPubMed
Leith, C.E. 1971 Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 28 (2), 145–161.10.1175/1520-0469(1971)028<0145:APATDT>2.0.CO;22.0.CO;2>CrossRefGoogle Scholar
Leith, C.E. & Kraichnan, R.H. 1972 Predictability of turbulent flows. J. Atmos. Sci. 29 (6), 1041–1058.10.1175/1520-0469(1972)029<1041:POTF>2.0.CO;22.0.CO;2>CrossRefGoogle Scholar
Leith, C.E. 1968 Diffusion approximation for two-dimensional turbulence. Phys. Fluids 11 (3), 671–672.10.1063/1.1691968CrossRefGoogle Scholar
Li, Y.C., Ho, R.D.J.G., Berera, A. & Feng, Z.C. 2020 Superfast amplification and superfast nonlinear saturation of perturbations as a mechanism of turbulence. J. Fluid Mech. 904, A27.10.1017/jfm.2020.715CrossRefGoogle Scholar
Lorenz, E.N. 1963 Deterministic nonperiodic flow. J. Atmos. Sci. 20 (2), 130–141.10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;22.0.CO;2>CrossRefGoogle Scholar
Mazzino, A. & Muratore-Ginanneschi, P. 2000 Passive scalar turbulence in high dimensions. Phys. Rev. E 63 (1), 015302.10.1103/PhysRevE.63.015302CrossRefGoogle ScholarPubMed
McComb, D. 2009 Scale-invariance and the inertial-range spectrum in three-dimensional stationary, isotropic turbulence. J. Phys. A: Math. Theor. 42 (12), 125501.10.1088/1751-8113/42/12/125501CrossRefGoogle Scholar
McComb, W.D., Yoffe, S.R., Linkmann, M.F. & Berera, A. 2014 Spectral analysis of structure functions and their scaling exponents in forced isotropic turbulence. Phys. Rev. E 90 (5), 053010.10.1103/PhysRevE.90.053010CrossRefGoogle ScholarPubMed
Meldi, M., Djenidi, L. & Antonia, R. 2018 Reynolds number effect on the velocity derivative flatness factor. J. Fluid Mech. 856, 426–443.10.1017/jfm.2018.717CrossRefGoogle Scholar
Mohan, P., Fitzsimmons, N. & Moser, R.D. 2017 Scaling of Lyapunov exponents in homogeneous isotropic turbulence. Phys. Rev. Fluids 2 (11), 114606.10.1103/PhysRevFluids.2.114606CrossRefGoogle Scholar
Mukherjee, S., Schalkwijk, J. & Jonker, H.J.J. 2016 Predictability of dry convective boundary layers: an LES study. J. Atmos. Sci. 73 (7), 2715–2727.10.1175/JAS-D-15-0206.1CrossRefGoogle Scholar
Nastac, G., Labahn, J.W., Magri, L. & Ihme, M. 2017 Lyapunov exponent as a metric for assessing the dynamic content and predictability of large-eddy simulations. Phys. Rev. Fluids 2 (9), 094606.10.1103/PhysRevFluids.2.094606CrossRefGoogle Scholar
Nelkin, M. 1974 Turbulence, critical fluctuations, and intermittency. Phys. Rev. A 9 (1), 388.10.1103/PhysRevA.9.388CrossRefGoogle Scholar
Nelkin, M. 1975 Scaling theory of hydrodynamic turbulence. Phys. Rev. A 11 (5), 1737.10.1103/PhysRevA.11.1737CrossRefGoogle Scholar
Orszag, S.A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41 (2), 363–386.10.1017/S0022112070000642CrossRefGoogle Scholar
Qian, J. 1994 Skewness factor of turbulent velocity derivative. Acta Mechanica Sin. 10 (1), 12–15.Google Scholar
Qian, J. 1997 Inertial range and the finite Reynolds number effect of turbulence. Phys. Rev. E 55 (1), 337.10.1103/PhysRevE.55.337CrossRefGoogle Scholar
Qian, J. 1998 Normal and anomalous scaling of turbulence. Phys. Rev. E 58 (6), 7325.10.1103/PhysRevE.58.7325CrossRefGoogle Scholar
Qian, J. 1999 Slow decay of the finite Reynolds number effect of turbulence. Phys. Rev. E 60 (3), 3409.10.1103/PhysRevE.60.3409CrossRefGoogle ScholarPubMed
Rose, H.A. & Sulem, P.L. 1978 Fully developed turbulence and statistical mechanics. J. Phys. 39 (5), 441–484.10.1051/jphys:01978003905044100CrossRefGoogle Scholar
Rozali, M., Sabag, E. & Yarom, A. 2018 Holographic turbulence in a large number of dimensions. J. High Energy Phys. 2018 (4), 65.10.1007/JHEP04(2018)065CrossRefGoogle Scholar
Ruelle, D. 1979 Microscopic fluctuations and turbulence. Phys. Lett. A 72 (2), 81–82.10.1016/0375-9601(79)90653-4CrossRefGoogle Scholar
Ruelle, D. & Takens, F. 1971 On the nature of turbulence. Commun. Math. Phys. 20 (3), 167–192.10.1007/BF01646553CrossRefGoogle Scholar
Schumacher, J., Sreenivasan, K.R. & Yakhot, V. 2007 Asymptotic exponents from low-Reynolds- number flows. New J. Phys. 9 (4), 89.10.1088/1367-2630/9/4/089CrossRefGoogle Scholar
Siggia, E.D. 1977 Origin of intermittency in fully developed turbulence. Phys. Rev. A 15 (4), 1730.10.1103/PhysRevA.15.1730CrossRefGoogle Scholar
Sinhuber, M., Bewley, G.P. & Bodenschatz, E. 2017 Dissipative effects on inertial-range statistics at high Reynolds numbers. Phys. Rev. Lett. 119 (13), 134502.10.1103/PhysRevLett.119.134502CrossRefGoogle ScholarPubMed
Suzuki, E., Nakano, T., Takahashi, N. & Gotoh, T. 2005 Energy transfer and intermittency in four-dimensional turbulence. Phys. Fluids 17 (8), 081702.10.1063/1.2001692CrossRefGoogle Scholar
Tang, S.L., Antonia, R.A., Djenidi, L., Danaila, L. & Zhou, Y. 2017 Finite Reynolds number effect on the scaling range behaviour of turbulent longitudinal velocity structure functions. J. Fluid Mech. 820, 341.10.1017/jfm.2017.218CrossRefGoogle Scholar
Tang, S.L., Antonia, R.A., Djenidi, L., Danaila, L. & Zhou, Y. 2018 Reappraisal of the velocity derivative flatness factor in various turbulent flows. J. Fluid Mech. 847, 244–265.10.1017/jfm.2018.307CrossRefGoogle Scholar
Tang, S., Antonia, R.A., Djenidi, L. & Zhou, Y. 2019 Can small-scale turbulence approach a quasi-universal state? Phys. Rev. Fluids 4 (2), 024607.10.1103/PhysRevFluids.4.024607CrossRefGoogle Scholar
Van Atta, C.W. & Chen, W.Y. 1970 Structure functions of turbulence in the atmospheric boundary layer over the ocean. J. Fluid Mech. 44 (1), 145–159.10.1017/S002211207000174XCrossRefGoogle Scholar
Verma, M.K. 2004 Statistical theory of magnetohydrodynamic turbulence: recent results. Phys. Rep. 401 (5–6), 229–380.10.1016/j.physrep.2004.07.007CrossRefGoogle Scholar
Wilson, K.G. & Fisher, M.E. 1972 Critical exponents in 3.99 dimensions. Phys. Rev. Lett. 28 (4), 240.10.1103/PhysRevLett.28.240CrossRefGoogle Scholar
Yakhot, V. 2001 Mean-field approximation and a small parameter in turbulence theory. Phys. Rev. E 63 (2), 026307.10.1103/PhysRevE.63.026307CrossRefGoogle Scholar
Yakhot, V. & Donzis, D. 2017 Emergence of multiscaling in a random-force stirred fluid. Phys. Rev. Lett. 119 (4), 044501.10.1103/PhysRevLett.119.044501CrossRefGoogle Scholar
Yamamoto, T., Shimizu, H., Inoshita, T., Nakano, T. & Gotoh, T. 2012 Local flow structure of turbulence in three, four, and five dimensions. Phys. Rev. E 86 (4), 046320.10.1103/PhysRevE.86.046320CrossRefGoogle ScholarPubMed
Yoffe, S.R. 2013 Investigation of the transfer and dissipation of energy in isotropic turbulence. arXiv:1306.3408.Google Scholar
Yoshimatsu, K. & Ariki, T. 2019 Error growth in three-dimensional homogeneous turbulence. J. Phys. Soc. Japan 88 (12), 124401.CrossRefGoogle Scholar