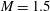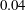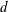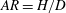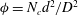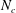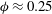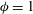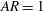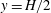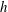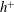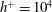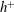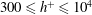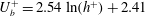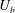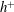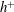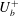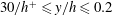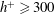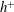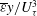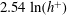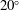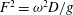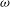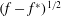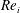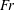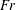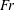Focus on Fluids
Predictions for the northern coast of the shear rheology map: XXLAOS
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
Instability and low-frequency unsteadiness in a shock-induced laminar separation bubble
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 5-26
-
- Article
- Export citation
Characterisation of drag and wake properties of canopy patches immersed in turbulent boundary layers
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 27-49
-
- Article
- Export citation
A nonlinear model for rotationally constrained convection with Ekman pumping
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 50-87
-
- Article
- Export citation
On the boundary layer structure near a highly permeable porous interface
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 88-139
-
- Article
- Export citation
Relationship between the energy dissipation function and the skin friction law in a turbulent channel flow
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 140-164
-
- Article
- Export citation
Squirmers with swirl: a model for Volvox swimming
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 165-186
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inertial-particle accelerations in turbulence: a Lagrangian closure
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 187-200
-
- Article
- Export citation
Oscillating line source in a shear flow with a free surface: critical layer-like contributions
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 201-231
-
- Article
- Export citation
Waves from an oscillating point source with a free surface in the presence of a shear current
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 232-255
-
- Article
- Export citation
New singularities for Stokes waves
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 256-283
-
- Article
- Export citation
Simulation of convection at a vertical ice face dissolving into saline water
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 284-298
-
- Article
- Export citation
Pseudo-turbulent heat flux and average gas–phase conduction during gas–solid heat transfer: flow past random fixed particle assemblies
-
- Published online by Cambridge University Press:
- 01 June 2016, pp. 299-349
-
- Article
- Export citation
The effect of shear-thinning behaviour on rod orientation in filled fluids
-
- Published online by Cambridge University Press:
- 01 June 2016, pp. 350-370
-
- Article
- Export citation
Three-dimensional instabilities in oscillatory flow past elliptic cylinders
-
- Published online by Cambridge University Press:
- 03 June 2016, pp. 371-397
-
- Article
- Export citation
Experiments on low-Reynolds-number turbulent flow through a square duct
-
- Published online by Cambridge University Press:
- 03 June 2016, pp. 398-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Drag reduction in numerical two-phase Taylor–Couette turbulence using an Euler–Lagrange approach
-
- Published online by Cambridge University Press:
- 06 June 2016, pp. 411-435
-
- Article
- Export citation
Interaction of turbulence with the leading-edge stagnation point of a thin aerofoil
-
- Published online by Cambridge University Press:
- 03 June 2016, pp. 436-456
-
- Article
- Export citation
Long wave propagation and run-up in converging bays
-
- Published online by Cambridge University Press:
- 03 June 2016, pp. 457-484
-
- Article
- Export citation
Conditions for validity of mean flow stability analysis
-
- Published online by Cambridge University Press:
- 06 June 2016, pp. 485-504
-
- Article
- Export citation