Research Papers
Availability of periodically inspected systems with Markovian wear and shocks
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 303-317
-
- Article
-
- You have access
- Export citation
Two-person red-and-black games with bet-dependent win probability functions
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 905-915
-
- Article
-
- You have access
- Export citation
Le Her with s Suits and d Denominations
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-15
-
- Article
-
- You have access
- Export citation
Research Article
An analysis of transient Markov decision processes
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 603-621
-
- Article
-
- You have access
- Export citation
Research Papers
Range of Asymptotic Behaviour of the Optimality Probability of the Expert and Majority Rules
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 16-31
-
- Article
-
- You have access
- Export citation
Average optimality for Markov decision processes in borel spaces: a new condition and approach
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 318-334
-
- Article
-
- You have access
- Export citation
A class of risk processes with delayed claims: ruin probability estimates under heavy tail conditions
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 916-926
-
- Article
-
- You have access
- Export citation
Research Article
Monotone utility convergence
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 622-633
-
- Article
-
- You have access
- Export citation
Derivatives pricing via p-optimal martingale measures: some extreme cases
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 634-651
-
- Article
-
- You have access
- Export citation
Research Papers
A Central Limit Theorem for Non-Overlapping Return Times
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 32-47
-
- Article
-
- You have access
- Export citation
The upcrossings index and the extremal index
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 927-937
-
- Article
-
- You have access
- Export citation
Boundedly rational quasi-Bayesian learning in coordination games with imperfect monitoring
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 335-350
-
- Article
-
- You have access
- Export citation
Research Article
The untraceable events method for absorbing processes
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 652-664
-
- Article
-
- You have access
- Export citation
Research Papers
Positive Dependence and Weak Convergence
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 48-59
-
- Article
-
- You have access
- Export citation
Central limit theorems for generalized Pólya urn models
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 938-951
-
- Article
-
- You have access
- Export citation
Structured coalescent with nonconservative migration
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 351-362
-
- Article
-
- You have access
- Export citation
A Diffusion Limit for Generalized Correlated Random Walks
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 60-73
-
- Article
-
- You have access
- Export citation
On the value function of the M/Cox(r)/1 queue
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 363-376
-
- Article
-
- You have access
- Export citation
An urn model arising from all-optical networks
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 952-966
-
- Article
-
- You have access
- Export citation
Research Article
Ultra-small scale-free geometric networks
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 665-677
-
- Article
-
- You have access
- Export citation



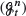 be a sequence of increasing filtrations converging to
be a sequence of increasing filtrations converging to 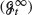 , and let
, and let 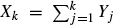 such that (
such that (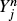 takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the
takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the