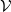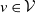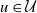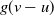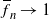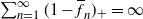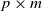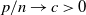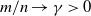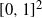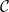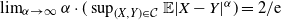FirstView articles
Original Article
Persistence of spectral projections for stochastic operators on large tensor products
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
(Almost) complete characterization of the stability of a discrete-time Hawkes process with inhibition and memory of length two
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-22
-
- Article
- Export citation
Bivariate tempered space-fractional Poisson process and shock models
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2024, pp. 1-17
-
- Article
- Export citation
Geometric random intersection graphs with general connection probabilities
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1-18
-
- Article
- Export citation
Depths in random recursive metric spaces
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-15
-
- Article
- Export citation
Series expansions for random disc-polygons in smooth plane convex bodies
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multivariate regularly varying insurance and financial risks in multidimensional risk models
- Part of:
-
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-24
-
- Article
- Export citation
Perturbation analysis for continuous-time Markov chains in a weak sense
- Part of:
-
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-23
-
- Article
- Export citation
Branching processes in nearly degenerate varying environment
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-20
-
- Article
- Export citation
Letter to the Editor
A remark on exact simulation of tempered stable Ornstein–Uhlenbeck processes
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1-3
-
- Article
-
- You have access
- HTML
- Export citation
Original Article
Recurrence and transience of a Markov chain on
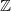 $\mathbb Z$+ and evaluation of prior distributions for a Poisson mean
$\mathbb Z$+ and evaluation of prior distributions for a Poisson mean
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-19
-
- Article
- Export citation
The limiting spectral distribution of large random permutation matrices
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
Buffon’s problem determines Gaussian curvature in three geometries
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coherent distributions on the square–extreme points and asymptotics
- Part of:
-
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-23
-
- Article
- Export citation
Super-replication of life-contingent options under the Black–Scholes framework
- Part of:
-
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-15
-
- Article
- Export citation
Constrained optimal stopping under a regime-switching model
- Part of:
-
- Published online by Cambridge University Press:
- 27 March 2024, pp. 1-20
-
- Article
- Export citation
Inequalities between time and customer averages for HNB(W)UE arrival processes
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-21
-
- Article
- Export citation
Asymptotic results for sums and extremes
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2024, pp. 1-19
-
- Article
- Export citation
Color-avoiding percolation and branching processes
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-25
-
- Article
- Export citation
Skew Ornstein–Uhlenbeck processes with sticky reflection and their applications to bond pricing
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-24
-
- Article
- Export citation