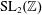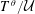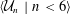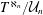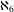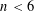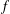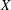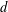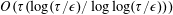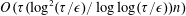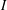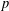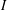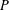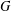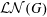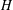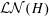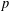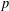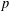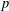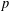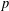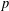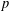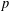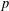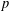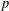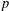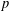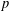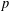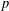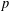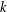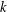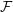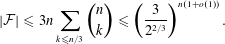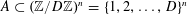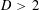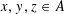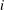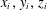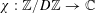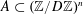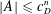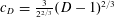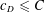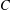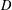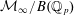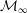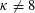Number Theory
Research Article
ZETA ELEMENTS IN DEPTH 3 AND THE FUNDAMENTAL LIE ALGEBRA OF THE INFINITESIMAL TATE CURVE
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2017, e1
-
- Article
-
- You have access
- Open access
- Export citation
Foundations
Research Article
REDUCED POWERS OF SOUSLIN TREES
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2017, e2
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
NONCLASSICAL SPECTRAL ASYMPTOTICS AND DIXMIER TRACES: FROM CIRCLES TO CONTACT MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2017, e3
-
- Article
-
- You have access
- Open access
- Export citation
Applied Analysis
Research Article
BREAKING THE COHERENCE BARRIER: A NEW THEORY FOR COMPRESSED SENSING
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2017, e4
-
- Article
-
- You have access
- Open access
- Export citation
Discrete Mathematics
Research Article
NONCROSSING SETS AND A GRASSMANN ASSOCIAHEDRON
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2017, e5
-
- Article
-
- You have access
- Open access
- Export citation
Differential Geometry and Geometric Analysis
Research Article
THE SPACE OF HYPERKÄHLER METRICS ON A 4-MANIFOLD WITH BOUNDARY
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2017, e6
-
- Article
-
- You have access
- Open access
- Export citation
Differential Equations
Research Article
SUFFICIENT CONDITIONS FOR THE EXISTENCE OF LIMITING CARLEMAN WEIGHTS
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2017, e7
-
- Article
-
- You have access
- Open access
- Export citation
Theoretical Computer Science
Research Article
EXPONENTIAL IMPROVEMENT IN PRECISION FOR SIMULATING SPARSE HAMILTONIANS
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2017, e8
-
- Article
-
- You have access
- Open access
- Export citation
Discrete Mathematics
Research Article
THE EXPECTED JAGGEDNESS OF ORDER IDEALS
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2017, e9
-
- Article
-
- You have access
- Open access
- Export citation
UNDECIDABILITY AND THE DEVELOPABILITY OF PERMUTOIDS AND RIGID PSEUDOGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2017, e10
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
LOCALLY NORMAL SUBGROUPS OF TOTALLY DISCONNECTED GROUPS. PART I: GENERAL THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2017, e11
-
- Article
-
- You have access
- Open access
- Export citation
LOCALLY NORMAL SUBGROUPS OF TOTALLY DISCONNECTED GROUPS. PART II: COMPACTLY GENERATED SIMPLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2017, e12
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
TRANSPORT PARALLÈLE ET CORRESPONDANCE DE SIMPSON
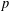 $p$-ADIQUE
$p$-ADIQUE
- Part of:
-
- Published online by Cambridge University Press:
- 19 June 2017, e13
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
Research Article
ESSENTIAL DIMENSION OF GENERIC SYMBOLS IN CHARACTERISTIC
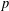 $p$
$p$
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2017, e14
-
- Article
-
- You have access
- Open access
- Export citation
Discrete Mathematics
Research Article
UPPER BOUNDS FOR SUNFLOWER-FREE SETS
- Part of:
-
- Published online by Cambridge University Press:
- 27 June 2017, e15
-
- Article
-
- You have access
- Open access
- Export citation
Probability
Research Article
SHORT TIME FULL ASYMPTOTIC EXPANSION OF HYPOELLIPTIC HEAT KERNEL AT THE CUT LOCUS
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2017, e16
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
A QUOTIENT OF THE LUBIN–TATE TOWER
- Part of:
-
- Published online by Cambridge University Press:
- 27 July 2017, e17
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Research Article
MINIMALITY AND MUTATION-EQUIVALENCE OF POLYGONS
-
- Published online by Cambridge University Press:
- 15 August 2017, e18
-
- Article
-
- You have access
- Open access
- Export citation
Probability
Research Article
ON THE REGULARITY OF SLE TRACE
- Part of:
-
- Published online by Cambridge University Press:
- 24 August 2017, e19
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Research Article
HYPERELLIPTIC GRAPHS AND METRIZED COMPLEXES
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2017, e20
-
- Article
-
- You have access
- Open access
- Export citation