Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-26T14:42:26.478Z Has data issue: false hasContentIssue false
  • English
  • Français

NONCLASSICAL SPECTRAL ASYMPTOTICS AND DIXMIER TRACES: FROM CIRCLES TO CONTACT MANIFOLDS

Part of: Spectral theory and eigenvalue problems CR manifolds Linear spaces and algebras of operators Infinite-dimensional manifolds

Published online by Cambridge University Press:  23 January 2017

HEIKO GIMPERLEIN  and
MAGNUS GOFFENG
HEIKO GIMPERLEIN
Affiliation:
Maxwell Institute for Mathematical Sciences and Department of Mathematics, Heriot-Watt University, Edinburgh EH14 4AS, UK Institute for Mathematics, University of Paderborn, Warburger Str. 100, 33098 Paderborn, Germany; h.gimperlein@hw.ac.uk
MAGNUS GOFFENG
Affiliation:
Department of Mathematical Sciences, Chalmers University of Technology and University of Gothenburg, SE-412 96 Gothenburg, Sweden; goffeng@chalmers.se

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the spectral behavior and noncommutative geometry of commutators 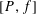$[P,f]$, where 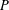$P$ is an operator of order 0 with geometric origin and 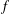$f$ a multiplication operator by a function. When 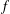$f$ is Hölder continuous, the spectral asymptotics is governed by singularities. We study precise spectral asymptotics through the computation of Dixmier traces; such computations have only been considered in less singular settings. Even though a Weyl law fails for these operators, and no pseudodifferential calculus is available, variations of Connes’ residue trace theorem and related integral formulas continue to hold. On the circle, a large class of nonmeasurable Hankel operators is obtained from Hölder continuous functions 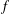$f$, displaying a wide range of nonclassical spectral asymptotics beyond the Weyl law. The results extend from Riemannian manifolds to contact manifolds and noncommutative tori.

MSC classification

Primary: 35P20: Asymptotic distribution of eigenvalues and eigenfunctions 58B34: Noncommutative geometry (à la Connes)
Secondary: 32V20: Analysis on CR manifolds 47L20: Operator ideals
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e3
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Abels, H., Pseudodifferential and Singular Integral Operators—An Introduction with Applications, De Gruyter Graduate Lectures (De Gruyter, Berlin, 2012).Google Scholar
Abels, H., ‘Pseudodifferential boundary value problems with nonsmooth coefficients’, Comm. Partial Differential Equations 30(10–12) (2005), 1463–1503.CrossRefGoogle Scholar
Beals, R. and Greiner, P., Calculus on Heisenberg Manifolds, Annals of Mathematics Studies, 119 (Princeton University Press, Princeton, NJ, 1988).Google Scholar
Bellaiche, A., ‘The tangent space in sub-Riemannian geometry’, inSub-Riemannian Geometry, Progress in Mathematics, 144 (Birkhäuser, Basel, 1996), 1–78.Google Scholar
Birman, M. S. and Solomyak, M. Z., ‘Asymptotic behavior of the spectrum of pseudo-differential operators with anisotropically homogeneous symbols’, Vestn. Leningrad. Univ. 13 (1977), 13–21. English translation in Vestn. Leningr. Univ. Math. 10 (1977), 237–247.Google Scholar
Birman, M. S. and Solomyak, M. Z., ‘Application of interpolational methods to estimates of the spectrum of integral operators’, in(Russian) Operator Theory in Function Spaces (Proc. School, Novosibirsk, 1975) (Russian) 341 (‘Nauka’ Sibirsk. Otdel., Novosibirsk, 1977), 42–70.Google Scholar
Bourgain, J. and Kahane, J.-P., ‘Sur les séries de Fourier des fonctions continues unimodulaires’, Ann. Inst. Fourier (Grenoble) 60(4) (2010), 1201–1214.Google Scholar
Brain, S., Mesland, B. and van Suijlekom, W. D., ‘Gauge theory for spectral triples and the unbounded Kasparov product’, J. Noncommut. Geom. 10(1) (2016), 135–206.Google Scholar
Calderón, A. P., ‘Commutators of singular integral operators’, Proc. Natl Acad. Sci. USA 53 (1965), 1092–1099.Google Scholar
Capogna, L., Danielli, D., Pauls, S. D. and Tyson, J. T., An Introduction to the Heisenberg Group and the Sub-Riemannian Isoperimetric Problem, (Birkhäuser, Basel, 2007).Google Scholar
Chen, Z., Xu, Q. and Yin, Z., ‘Harmonic analysis on quantum tori’, Comm. Math. Phys. 322(3) (2013), 755–805.Google Scholar
Christ, M., ‘A T (b) theorem with remarks on analytic capacity and the Cauchy integral’, Colloq. Math. 60/61(2) (1990), 601–628.CrossRefGoogle Scholar
Coifman, R. and Meyer, Y., ‘Commutateurs d’integrales singulieres et operateurs multilineaires’, Ann. Inst. Fourier (Grenoble) 28 (1978), 177–202.Google Scholar
Connes, A., ‘The action functional in noncommutative geometry’, Comm. Math. Phys. 117(4) (1988), 673–683.CrossRefGoogle Scholar
Connes, A., Noncommutative Geometry, (Academic Press, London, 1994).Google Scholar
Connes, A. and Karoubi, M., ‘Caractere multiplicatif d’un module de Fredholm’, J. K-Theory 2(3) (1988), 431–463.Google Scholar
Connes, A. and Landi, G., ‘Noncommutative manifolds, the instanton algebra and isospectral deformations’, Comm. Math. Phys. 221(1) (2001), 141–159.Google Scholar
Connes, A., Sullivan, D. and Teleman, N., ‘Quasiconformal mappings, operators on Hilbert space, and local formulae for characteristic classes’, Topology 33(4) (1994), 663–681.Google Scholar
Engliš, M. and Rochberg, R., ‘The Dixmier trace of Hankel operators on the Bergman space’, J. Funct. Anal. 257(5) (2009), 1445–1479.CrossRefGoogle Scholar
Engliš, M. and Zhang, G., ‘Hankel operators and the Dixmier trace on strictly pseudoconvex domains’, Doc. Math. 15 (2010), 601–622.CrossRefGoogle Scholar
Engliš, M. and Zhang, G., ‘Hankel operators and the Dixmier trace on the Hardy space’, J. Lond. Math. Soc. (2) 94 (2016), 337–356.Google Scholar
Feldman, M. and Rochberg, R., ‘Singular value estimates for commutators and Hankel operators on the unit ball and the Heisenberg group’, inAnalysis and Partial Differential Equations, Lecture Notes in Pure and Applied Mathematics, 122 (Dekker, New York, 1990), 121–159.Google Scholar
Folland, G. B., ‘Compact Heisenberg manifolds as CR manifolds’, J. Geom. Anal. 14(3) (2004), 521–532.Google Scholar
Folland, G. B. and Stein, E. M., Hardy Spaces on Homogeneous Groups, Mathematical Notes, 28 (Princeton University Press, Princeton, NJ, 1982), University of Tokyo Press, Tokyo.Google Scholar
Gimperlein, H. and Goffeng, M., ‘Commutator estimates on contact manifolds and applications’, Preprint, 2013, arXiv:1312.7677.Google Scholar
Goffeng, M., ‘Analytic formulas for topological degree of nonsmooth mappings: the odd-dimensional case’, Adv. Math. 231 (2012), 357–377.Google Scholar
Grubb, G., ‘Spectral asymptotics for nonsmooth singular Green operators’, Comm. Partial Differential Equations 39(3) (2014), 530–573.Google Scholar
Johnsen, J., ‘Pointwise multiplication of Besov and Triebel–Lizorkin spaces’, Math. Nachr. 175 (1995), 85–133.CrossRefGoogle Scholar
Kaad, J., ‘Comparison of secondary invariants of algebraic K-theory’, J. K-Theory 8(1) (2011), 169–182.Google Scholar
Kahane, J.-P., ‘Winding numbers and Fourier series’, Tr. Mat. Inst. Steklova 273 (2011), 207–211. Sovremennye Problemy Matematiki; translation in Proc. Steklov Inst. Math. 273(1) (2011) 191–195.Google Scholar
Kalton, N., Lord, S., Potapov, D. and Sukochev, F., ‘Traces of compact operators and the noncommutative residue’, Adv. Math. 235 (2013), 1–55.Google Scholar
Lord, S., Sukochev, F. and Zanin, D., ‘Singular traces’, inTheory and Applications, de Gruyter Studies in Mathematics, 46 (De Gruyter, Berlin, 2013).Google Scholar
Marschall, J., ‘Pseudodifferential operators with nonregular symbols of the class S 𝜌, 𝛿 m ’, Comm. Partial Differential Equations 12(8) (1987), 921–965.Google Scholar
Meyerson, W., ‘Lipschitz and bilipschitz maps on Carnot groups’, Pacific J. Math. 263(1) (2013), 143–170.Google Scholar
Peller, V. V., Hankel Operators and Their Applications, Springer Monographs in Mathematics (Springer, New York, 2003).Google Scholar
Pietsch, A., ‘Connes-Dixmier versus Dixmier traces’, Integral Equations Operator Theory 77(2) (2013), 243–259.Google Scholar
Pietsch, A., ‘Traces and residues of pseudo-differential operators on the torus’, Integral Equations Operator Theory 83(1) (2015), 1–23.Google Scholar
Ponge, R., ‘Noncommutative residue for Heisenberg manifolds. Applications in CR and contact geometry’, J. Funct. Anal. 252(2) (2007), 399–463.CrossRefGoogle Scholar
Ponge, R., ‘Heisenberg calculus and spectral theory of hypoelliptic operators on Heisenberg manifolds’, Mem. Amer. Math. Soc. 194(906) (2008), viii + 134 pp.Google Scholar
Pushnitski, A. and Yafaev, D., ‘Asymptotic behavior of eigenvalues of Hankel operators’, Int. Math. Res. Not. (IMRN) 22 (2015), 11861–11886.Google Scholar
Rochberg, R. and Semmes, S., ‘End point results for estimates of singular values of singular integral operators’, inContributions to Operator Theory and its Applications (Mesa, AZ, 1987), Oper. Theory Adv. Appl., 35 (Birkhäuser, Basel, 1988), 217–231.CrossRefGoogle Scholar
Rochberg, R. and Semmes, S., ‘Nearly weakly orthonormal sequences, singular value estimates, and Calderon–Zygmund operators’, J. Funct. Anal. 86(2) (1989), 237–306.Google Scholar
Russo, B., ‘On the Hausdorff-Young theorem for integral operators’, Pacific J. Math. 68(1) (1977), 241–253.CrossRefGoogle Scholar
Sedaev, A. A., Sukochev, F. and Zanin, D. V., ‘Lidskii-type formulae for Dixmier traces’, Integral Equations Operator Theory 68(4) (2010), 551–572.CrossRefGoogle Scholar
Sukochev, F., Usachev, A. and Zanin, D., ‘On the distinction between the classes of Dixmier and Connes–Dixmier traces’, Proc. Amer. Math. Soc. 141(6) (2013), 2169–2179.Google Scholar
Simon, B., Trace Ideals and Their Applications, 2nd edn, Mathematical Surveys and Monographs, 120 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Stein, E. M., Singular Integrals and Differentiability Properties of Functions, Princeton Mathematical Series, 30 (Princeton University Press, Princeton, NJ, 1970).Google Scholar
Taylor, M. E., Pseudodifferential Operators and Nonlinear PDE, Progress in Mathematics, 100 (Birkhäuser Boston, Inc., Boston, MA, 1991), 213 pp. ISBN: 0-8176-3595-5.CrossRefGoogle Scholar
Taylor, M. E., Tools for PDE, Mathematical Surveys and Monographs, 81 (AMS, Providence, RI, 2000).Google Scholar
Taylor, M. E., ‘Commutator estimates for Hölder continuous and $bmo$ -Sobolev multipliers’, Preprint.Google Scholar
Weaver, N., ‘Lipschitz algebras and derivations of von Neumann algebras’, J. Funct. Anal. 139(2) (1996), 261–300.Google Scholar
Xiong, X., Xu, Q. and Yin, Z., Sobolev, Besov and Triebel–Lizorkin spaces on quantum tori, arXiv:1507.01789, to appear in Memoirs of AMS.Google Scholar
Yamashita, M., ‘Connes-Landi deformation of spectral triples’, Lett. Math. Phys. 94(3) (2010), 263–291.CrossRefGoogle Scholar
Zygmund, A., Trigonometric Series, 3rd edn, Vol. I. (Cambridge Mathematical Library. Cambridge University Press, Cambridge, 2002).Google Scholar