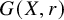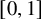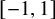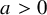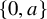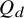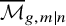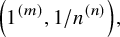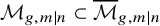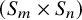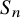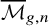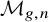Open access
Algebra
Affine Bruhat order and Demazure products
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability
An extension of the stochastic sewing lemma and applications to fractional stochastic calculus
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2024, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Generic Beauville’s Conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2024, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Foundations
Generic Stability Independence and Treeless Theories
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2024, e49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability
A remark on Gibbs measures with log-correlated Gaussian fields
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2024, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Applied Analysis
Stability of isometric immersions of hypersurfaces
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2024, e43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Whittaker categories of quasi-reductive lie superalgebras and quantum symmetric pairs
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2024, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Lower Bounds for the Canonical Height of a Unicritical Polynomial and Capacity
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2024, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Evaluation of
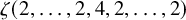 $ \zeta (2,\ldots ,2,4,2,\ldots ,2) $ and period polynomial relations
$ \zeta (2,\ldots ,2,4,2,\ldots ,2) $ and period polynomial relations
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2024, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Extensions of the colorful Helly theorem for d-collapsible and d-Leray complexes
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2024, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Cohomological Descent for Faltings Ringed Topos
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2024, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Cohomological
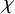 $\chi $-dependence of ring structure for the moduli of one-dimensional sheaves on
$\chi $-dependence of ring structure for the moduli of one-dimensional sheaves on 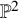 $\mathbb {P}^2$
$\mathbb {P}^2$
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2024, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-stable smooth Fano threefolds of Picard rank two
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2024, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Polypositroids
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2024, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Finite skew braces of square-free order and supersolubility
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2024, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Undecidability of polynomial inequalities in weighted graph homomorphism densities
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2024, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Turán number of the hypercube
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2024, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability
Asymptotic expansions relating to the distribution of the length of longest increasing subsequences
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2024, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Equivariant Hodge polynomials of heavy/light moduli spaces
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2024, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Foundations
Structural, point-free, non-Hausdorff topological realization of Borel groupoid actions
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2024, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation



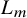
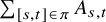
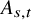
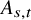
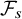
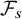
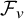
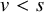
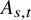
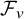
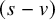
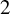
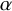
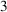
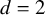
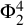
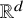
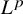
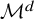
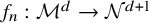
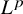
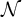
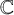
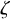
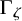

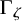
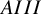
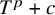
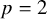
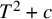
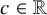
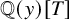
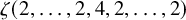
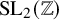
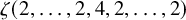
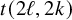
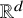
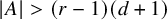

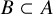
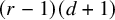
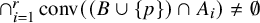
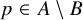
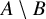
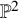
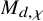
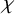
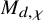
 and
and 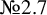 are K-stable, and we also prove that smooth Fano threefolds in the family
are K-stable, and we also prove that smooth Fano threefolds in the family 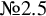 that satisfy one very explicit generality condition are K-stable.
that satisfy one very explicit generality condition are K-stable.