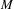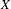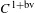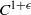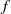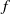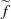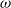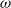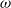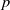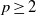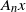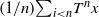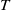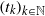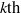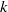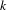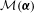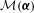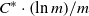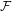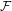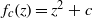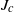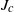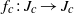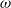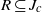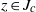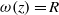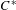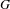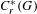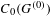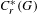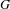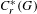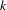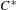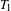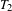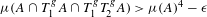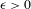Research Article
Dynamical versus diffraction spectrum for structures with finite local complexity
-
- Published online by Cambridge University Press:
- 05 August 2014, pp. 2017-2043
-
- Article
- Export citation
Classification and rigidity of totally periodic pseudo-Anosov flows in graph manifolds
-
- Published online by Cambridge University Press:
- 03 July 2014, pp. 1681-1722
-
- Article
- Export citation
Structure of transition classes for factor codes on shifts of finite type
-
- Published online by Cambridge University Press:
- 07 August 2014, pp. 2353-2370
-
- Article
- Export citation
Dynamics of iterated function systems on the circle close to rotations
-
- Published online by Cambridge University Press:
- 23 April 2014, pp. 1345-1368
-
- Article
- Export citation
Area-preserving diffeomorphisms of the torus whose rotation sets have non-empty interior
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 1-33
-
- Article
- Export citation
Limit sets of stable cellular automata
-
- Published online by Cambridge University Press:
- 09 October 2013, pp. 673-690
-
- Article
- Export citation
The
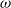 $\omega $-limit sets of quadratic Julia sets
$\omega $-limit sets of quadratic Julia sets
-
- Published online by Cambridge University Press:
- 27 September 2013, pp. 337-358
-
- Article
- Export citation
Oscillation and the mean ergodic theorem for uniformly convex Banach spaces
-
- Published online by Cambridge University Press:
- 10 January 2014, pp. 1009-1027
-
- Article
- Export citation
Difference sets and frequently hypercyclic weighted shifts
-
- Published online by Cambridge University Press:
- 13 November 2013, pp. 691-709
-
- Article
- Export citation
Topological and algebraic reducibility for patterns on trees
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 34-63
-
- Article
- Export citation
Symbol ratio minimax sequences in the lexicographic order
-
- Published online by Cambridge University Press:
- 05 August 2014, pp. 2371-2396
-
- Article
- Export citation
Li–Yorke chaos in linear dynamics
-
- Published online by Cambridge University Press:
- 10 July 2014, pp. 1723-1745
-
- Article
- Export citation
Rigorous pointwise approximations for invariant densities of non-uniformly expanding maps
-
- Published online by Cambridge University Press:
- 10 January 2014, pp. 1028-1044
-
- Article
-
- You have access
- Export citation
On the geometry of bifurcation currents for quadratic rational maps
-
- Published online by Cambridge University Press:
- 14 March 2014, pp. 1369-1379
-
- Article
- Export citation
Chain transitivity and variations of the shadowing property
-
- Published online by Cambridge University Press:
- 03 July 2014, pp. 2044-2052
-
- Article
- Export citation
Unimodular random trees
-
- Published online by Cambridge University Press:
- 20 August 2013, pp. 359-373
-
- Article
- Export citation
Shadowing and
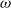 $\omega $-limit sets of circular Julia sets
$\omega $-limit sets of circular Julia sets
-
- Published online by Cambridge University Press:
- 14 November 2013, pp. 1045-1055
-
- Article
- Export citation
Purely infinite
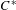 $C^{\ast }$-algebras associated to étale groupoids
$C^{\ast }$-algebras associated to étale groupoids
-
- Published online by Cambridge University Press:
- 04 August 2014, pp. 2397-2411
-
- Article
- Export citation
Lower bound in the Roth theorem for amenable groups
-
- Published online by Cambridge University Press:
- 03 July 2014, pp. 1746-1766
-
- Article
- Export citation
Tubular neighborhoods and continuation of Morse decompositions
-
- Published online by Cambridge University Press:
- 03 July 2014, pp. 2053-2079
-
- Article
- Export citation