Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-20T00:04:09.373Z Has data issue: false hasContentIssue false
  • English
  • Français

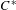Purely infinite $C^{\ast }$-algebras associated to étale groupoids

Published online by Cambridge University Press:  04 August 2014

JONATHAN BROWN ,
LISA ORLOFF CLARK  and
ADAM SIERAKOWSKI
JONATHAN BROWN
Affiliation:
Department of Mathematics, University of Dayton, 300 College Park, Dayton, OH 45469-2316, USA email jonathan.henry.brown@gmail.com
LISA ORLOFF CLARK
Affiliation:
Department of Mathematics and Statistics, University of Otago, PO Box 56, Dunedin 9054, New Zealand email lclark@maths.otago.ac.nz
ADAM SIERAKOWSKI
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, NSW 2522, Australia email asierako@uow.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

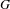Let $G$ be a Hausdorff, étale groupoid that is minimal and topologically principal. We show that 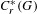$C_{r}^{\ast }(G)$ is purely infinite simple if and only if all the non-zero positive elements of 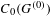$C_{0}(G^{(0)})$ are infinite in 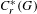$C_{r}^{\ast }(G)$. If 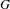$G$ is a Hausdorff, ample groupoid, then we show that 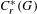$C_{r}^{\ast }(G)$ is purely infinite simple if and only if every non-zero projection in 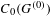$C_{0}(G^{(0)})$ is infinite in 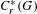$C_{r}^{\ast }(G)$. We then show how this result applies to 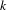$k$-graph 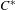$C^{\ast }$-algebras. Finally, we investigate strongly purely infinite groupoid 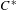$C^{\ast }$-algebras.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 8 , December 2015 , pp. 2397 - 2411
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman-Delaroche, C.. Purely infinite C ∗ -algebras arising from dynamical system. Bull. Soc. Math. France 125(2) (1997), 199–225.CrossRefGoogle Scholar
Anantharaman-Delaroche, C. and Renault, J.. Amenable Groupoids (Monographies de L’Enseignement Mathématique, 36). L’Enseignement Mathématique, Geneva, 2000.Google Scholar
Blackadar, B.. Operator algebras. Encyclopaedia of Mathematical Sciences (Theory of C ∗ -algebras and von Neumann Algebras, Operator Algebras and Non-commutative Geometry, III). Springer, Berlin, 2006, 122.Google Scholar
Brown, J. H., Clark, L. O., Farthing, C. and Sims, A.. Simplicity of algebras associated to étale groupoids. Semigroup Forum 88 (2014), 433–452.CrossRefGoogle Scholar
Carlsen, T. and Thomsen, K.. The structure of the C ∗ -algebra of a locally injective surjection. Ergod. Th. & Dynam. Sys. 32(2) (2012), 1226–1248.CrossRefGoogle Scholar
Clark, L. O., Farthing, C., Sims, A. and Tomforde, M.. A groupoid generalization of Leavitt path algebras. Semigroup Forum (2014), doi:10.1007/s00233-014-9594-z.CrossRefGoogle Scholar
Cuntz, J.. K-theory for certain C ∗ -algebras. Ann. of Math. (2) 113(1) (1981), 181–197.CrossRefGoogle Scholar
Elliott, G.. On the classification of C ∗ -algebras of real rank zero. J. Reine Angew. Math. 443 (1993), 179–219.Google Scholar
Exel, R.. Reconstructing a totally disconnected groupoid from its ample semigroup. Proc. Amer. Math. Soc. 138 (2010), 2991–3001.CrossRefGoogle Scholar
Giordano, T. and Sierakowski, A.. Purely infinite partial crossed products. J. Funct. Anal. 266 (2014), 5733–5764.CrossRefGoogle Scholar
Kirchberg, E.. The classification of purely infinite $C^{\ast }$-algebras using Kasparov’s theory. Preprint, 1994.Google Scholar
Kirchberg, E.. Das nicht-kommutative Michael-Auswahlprinzip und die Klassifikation nicht-einfacher Algebren. C ∗ -Algebras (Proceedings of the SFB-Workshop on C ∗ -algebras, Münster, Germany, March 8–12, 1999). Eds. Cuntz, J. and Echterhoff, S.. Springer, Berlin, 2000, pp. 92–141.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M.. Infinite non-simple C ∗ -algebras: absorbing the Cuntz algebras 𝓞∞. Adv. Math. 167 (2002), 195–264.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M.. Non-simple purely infinite C ∗ -algebras. Amer. J. Math. 122 (2000), 637–666.CrossRefGoogle Scholar
Kirchberg, E. and Sierakowski, A.. Strong pure infiniteness of crossed products, submitted. Preprint,arXiv:13125195.Google Scholar
Kumjian, A. and Pask, D.. Higher rank graph C ∗ -algebras. New York J. Math. 6 (2000), 1–20.Google Scholar
Kumjian, A., Pask, D. and Raeburn, I.. Cuntz–Krieger algebras of directed graphs. Pacific J. Math. 184(1) (1998), 161–174.CrossRefGoogle Scholar
Muhly, P. S., Renault, J. and Williams, D. P.. Continuous trace groupoid C ∗ -algebras, III. Trans. Amer. Math. Soc. 348 (1996), 3621–3641.CrossRefGoogle Scholar
Phillips, N. C.. A classification theorem for nuclear purely infinite simple C ∗ -algebras. Doc. Math. 5 (2000), 49–114.CrossRefGoogle Scholar
Renault, J.. A Groupoid Approach to C ∗ -algebras (Lecture Notes in Mathematics, 793). Springer, Berlin, 1980.CrossRefGoogle Scholar
Renault, J.. The ideal structure of groupoid crossed product C ∗ -algebras. J. Operator Theory 25 (1991), 3–36.Google Scholar
Robertson, D. I. and Sims, A.. Simplicity of C ∗ -algebras associated to higher-rank graphs. Bull. Lond. Math. Soc. 39 (2007), 337–344.CrossRefGoogle Scholar
Rørdam, M. and Sierakowski, A.. Purely infinite C ∗ -algebras arising from crossed products. Ergod. Th. & Dynam. Sys. 32(1) (2012), 273–293.CrossRefGoogle Scholar
Sims, A.. Gauge-invariant ideals in the C ∗ -algebras of finitely aligned higher-rank graphs. Canad. J. Math. 58 (2006), 1268–1290.CrossRefGoogle Scholar
Spielberg, J.. Graph-based models for Kirchberg algebras. J. Operator Theory 57 (2007), 347–374.Google Scholar
Steinberg, B.. A groupoid approach to inverse semigroup algebras. Adv. Math. 223 (2010), 689–727.CrossRefGoogle Scholar