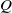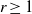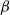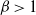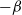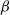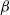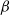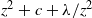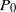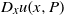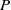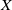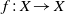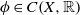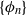Research Article
On the trigonometric moment problem
-
- Published online by Cambridge University Press:
- 16 November 2012, pp. 1-20
-
- Article
- Export citation
Actions of amenable equivalence relations on CAT(0) fields
-
- Published online by Cambridge University Press:
- 30 October 2012, pp. 21-54
-
- Article
- Export citation
Asymptotic structure in substitution tiling spaces
-
- Published online by Cambridge University Press:
- 27 September 2012, pp. 55-94
-
- Article
- Export citation
A Juzvinskii addition theorem for finitely generated free group actions
-
- Published online by Cambridge University Press:
- 01 November 2012, pp. 95-109
-
- Article
- Export citation
Measure-theoretic chaos
-
- Published online by Cambridge University Press:
- 31 August 2012, pp. 110-131
-
- Article
- Export citation
Non-recurrence sets for weakly mixing linear dynamical systems
-
- Published online by Cambridge University Press:
- 24 August 2012, pp. 132-152
-
- Article
- Export citation
Isomorphisms between positive and negative
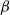 $\beta $-transformations
$\beta $-transformations
-
- Published online by Cambridge University Press:
- 09 November 2012, pp. 153-170
-
- Article
- Export citation
Julia sets converging to filled quadratic Julia sets
-
- Published online by Cambridge University Press:
- 21 August 2012, pp. 171-184
-
- Article
- Export citation
Viscous stability of quasi-periodic tori
-
- Published online by Cambridge University Press:
- 27 November 2012, pp. 185-210
-
- Article
- Export citation
Templates for geodesic flows
-
- Published online by Cambridge University Press:
- 28 November 2012, pp. 211-235
-
- Article
- Export citation
Wild Milnor attractors accumulated by lower-dimensional dynamics
-
- Published online by Cambridge University Press:
- 05 November 2012, pp. 236-262
-
- Article
- Export citation
A subgroup formula for f-invariant entropy
-
- Published online by Cambridge University Press:
- 30 November 2012, pp. 263-298
-
- Article
- Export citation
The cohomological equation and invariant distributions for horocycle maps
-
- Published online by Cambridge University Press:
- 03 December 2012, pp. 299-340
-
- Article
- Export citation
Fundamental domain of invariant sets and applications
-
- Published online by Cambridge University Press:
- 02 November 2012, pp. 341-352
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 34 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 January 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
ETS volume 34 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 January 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation