Hostname: page-component-77c89778f8-5wvtr Total loading time: 0 Render date: 2024-07-16T17:39:39.587Z Has data issue: false hasContentIssue false
  • English
  • Français

The cohomological equation and invariant distributions for horocycle maps

Published online by Cambridge University Press:  03 December 2012

JAMES TANIS
JAMES TANIS*
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD, USA (email: jtanis@rice.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the invariant distributions for horocycle maps on 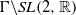$\Gamma \backslash SL(2, \mathbb {R})$and prove Sobolev estimates for the cohomological equation of horocycle maps. As an application, we obtain a rate of equidistribution for horocycle maps on compact manifolds.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 1 , February 2014 , pp. 299 - 340
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Burger, M.. Horocycle flow on geometrically finite surfaces. Duke Math. J. 6 (1990), 779–803.Google Scholar
[2]Flaminio, L. and Forni, G.. Invariant distributions and time averages for horocycle flows. Duke Math. J. 119(3) (2003), 465–526.Google Scholar
[3]Flaminio, L. and Forni, G.. Equidistribution of nilflows with application to theta sums. Ergod. Th. & Dynam. Sys. 26 (2006), 409–433.Google Scholar
[4]Forni, G.. Solutions of the cohomological equation for area preserving flows on surfaces of higher genus. Ann. of Math. (2) 146 (1997), 295–344.Google Scholar
[5]Furstenberg, H.. Unique ergodicity of the horocycle flow. Recent Advances in Topological Dynamics (Lecture Notes in Mathematics, 318). Springer, Berlin, 1973, pp. 95–115.Google Scholar
[6]Lions, J.. Non-homogeneous Boundary Value Problems and Applications. Vol 1. Springer, New York, 1972.Google Scholar
[7]Mautner, F.. Unitary representations of locally compact groups. I. Ann. of Math. (2) 51 (1950), 1–25.Google Scholar
[8]Mieczkowski, D.. The first cohomology of parabolic actions for some higher-rank abelian groups and representation theory. J. Mod. Dyn. 1(1) (2007), 61–92.Google Scholar
[9]Moore, C.. Exponential decay of correlation coefficients for geodesic flows. Group Representations, Ergodic Theory, Operator Algebras and Mathematical Physics (Mathematical Sciences Research Institute Publications, 6). Springer, New York, 1987, pp. 163–181.Google Scholar
[10]Nelson, E.. Analytic vectors. Ann. of Math. (2) 70 (1959), 572–615.Google Scholar
[11]Ratner, M.. The rate of mixing for geodesic and horocycle flows. Ergod. Th. & Dynam. Sys. 7 (1987), 267–288.CrossRefGoogle Scholar
[12]Sarnak, P.. Selberg’s eigenvalue conjecture. Notices Amer. Math. Soc. 42 (1995), 1272–1277.Google Scholar
[13]Sarnak, P. and Ubis, A.. The horocycle flow at prime times. Preprint, arXiv:1110.0777v1.Google Scholar
[14]Venkatesh, A.. Sparse equidistribution problems, period bounds and subconvexity. Ann. of Math. (2) 172 (2010), 989–1094.Google Scholar