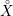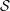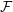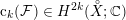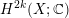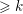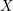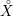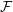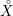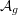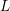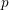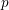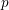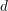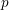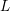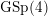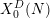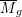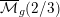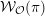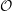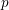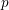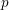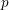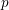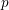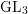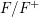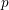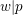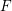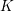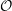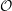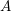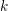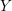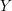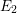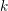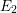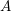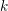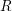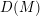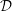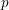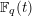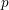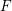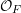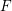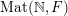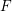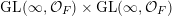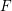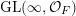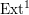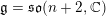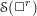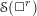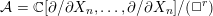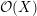Research Article
Goresky–Pardon lifts of Chern classes and associated Tate extensions
- Part of:
-
- Published online by Cambridge University Press:
- 03 May 2017, pp. 1349-1371
-
- Article
-
- You have access
- HTML
- Export citation
Régulateurs modulaires explicites via la méthode de Rogers–Zudilin
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2017, pp. 1119-1152
-
- Article
-
- You have access
- HTML
- Export citation
Minimal weights of Hilbert modular forms in characteristic
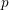 $p$
$p$
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2017, pp. 1769-1778
-
- Article
-
- You have access
- HTML
- Export citation
On higher regulators of Siegel threefolds II: the connection to the special value
- Part of:
-
- Published online by Cambridge University Press:
- 27 March 2017, pp. 889-946
-
- Article
-
- You have access
- HTML
- Export citation
Equations of hyperelliptic Shimura curves
- Part of:
-
- Published online by Cambridge University Press:
- 19 January 2017, pp. 1-40
-
- Article
-
- You have access
- HTML
- Export citation
Second flip in the Hassett–Keel program: a local description
- Part of:
-
- Published online by Cambridge University Press:
- 18 May 2017, pp. 1547-1583
-
- Article
-
- You have access
- HTML
- Export citation
Generalized and degenerate Whittaker models
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2017, pp. 223-256
-
- Article
-
- You have access
- HTML
- Export citation
The
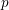 $p$-adic Gross–Zagier formula on Shimura curves
$p$-adic Gross–Zagier formula on Shimura curves
- Part of:
-
- Published online by Cambridge University Press:
- 11 July 2017, pp. 1987-2074
-
- Article
-
- You have access
- HTML
- Export citation
On mod
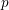 $p$ local-global compatibility for
$p$ local-global compatibility for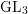 $\text{GL}_{3}$ in the ordinary case
$\text{GL}_{3}$ in the ordinary case
- Part of:
-
- Published online by Cambridge University Press:
- 25 August 2017, pp. 2215-2286
-
- Article
-
- You have access
- HTML
- Export citation
Une nouvelle approche dans la théorie des entiers friables
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2017, pp. 453-473
-
- Article
-
- You have access
- HTML
- Export citation
Equivariant
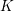 $K$-theory of Grassmannians II: the Knutson–Vakil conjecture
$K$-theory of Grassmannians II: the Knutson–Vakil conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 09 March 2017, pp. 667-677
-
- Article
-
- You have access
- HTML
- Export citation
On categories
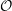 ${\mathcal{O}}$ for quantized symplectic resolutions
${\mathcal{O}}$ for quantized symplectic resolutions
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2017, pp. 2445-2481
-
- Article
-
- You have access
- HTML
- Export citation
On the de Rham homology and cohomology of a complete local ring in equicharacteristic zero
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2017, pp. 2075-2146
-
- Article
-
- You have access
- HTML
- Export citation
Non-abelian Cohen–Lenstra heuristics over function fields
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2017, pp. 1372-1390
-
- Article
-
- You have access
- HTML
- Export citation
Lagrangian embeddings of cubic fourfolds containing a plane
- Part of:
-
- Published online by Cambridge University Press:
- 23 March 2017, pp. 947-972
-
- Article
-
- You have access
- HTML
- Export citation
Ergodic measures on spaces of infinite matrices over non-Archimedean locally compact fields
- Part of:
-
- Published online by Cambridge University Press:
- 11 September 2017, pp. 2482-2533
-
- Article
-
- You have access
- HTML
- Export citation
Cluster categories for marked surfaces: punctured case
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2017, pp. 1779-1819
-
- Article
-
- You have access
- HTML
- Export citation
Higher symmetries of powers of the Laplacian and rings of differential operators
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2017, pp. 678-716
-
- Article
-
- You have access
- HTML
- Export citation
On quasi-classical limits of DQ-algebroids
- Part of:
-
- Published online by Cambridge University Press:
- 19 January 2017, pp. 41-67
-
- Article
-
- You have access
- HTML
- Export citation
Finiteness of fundamental groups
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2017, pp. 257-273
-
- Article
-
- You have access
- HTML
- Export citation