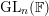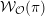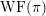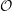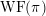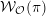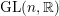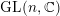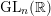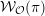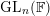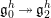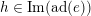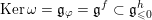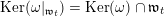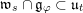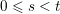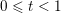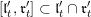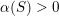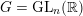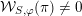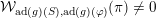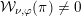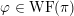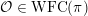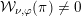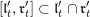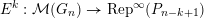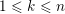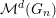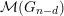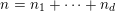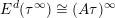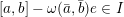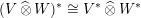1 Introduction and main results
1.1 General results
Let
![]() $\mathbb{F}$
be a local field of characteristic zero,
$\mathbb{F}$
be a local field of characteristic zero,
![]() $G$
a reductive group defined over
$G$
a reductive group defined over
![]() $\mathbb{F}$
,
$\mathbb{F}$
,
![]() $\mathfrak{g}$
its Lie algebra and
$\mathfrak{g}$
its Lie algebra and
![]() $\mathfrak{g}^{\ast }$
the dual space to
$\mathfrak{g}^{\ast }$
the dual space to
![]() $\mathfrak{g}$
. A Whittaker pair is an ordered pair
$\mathfrak{g}$
. A Whittaker pair is an ordered pair
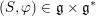 $(S,\unicode[STIX]{x1D711})\in \mathfrak{g}\times \mathfrak{g}^{\ast }$
such that
$(S,\unicode[STIX]{x1D711})\in \mathfrak{g}\times \mathfrak{g}^{\ast }$
such that
![]() $S$
is semi-simple with eigenvalues of the adjoint action
$S$
is semi-simple with eigenvalues of the adjoint action
![]() $\text{ad}(S)$
lying in
$\text{ad}(S)$
lying in
![]() $\mathbb{Q}$
, and
$\mathbb{Q}$
, and
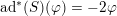 $\text{ad}^{\ast }(S)(\unicode[STIX]{x1D711})=-2\unicode[STIX]{x1D711}$
. Note that
$\text{ad}^{\ast }(S)(\unicode[STIX]{x1D711})=-2\unicode[STIX]{x1D711}$
. Note that
![]() $\unicode[STIX]{x1D711}$
is necessarily nilpotent and given by the Killing form pairing with a (unique) nilpotent element
$\unicode[STIX]{x1D711}$
is necessarily nilpotent and given by the Killing form pairing with a (unique) nilpotent element
 $f=f_{\unicode[STIX]{x1D711}}\in \mathfrak{g}$
. Following [Reference Moeglin and WaldspurgerMW87] we attach to
$f=f_{\unicode[STIX]{x1D711}}\in \mathfrak{g}$
. Following [Reference Moeglin and WaldspurgerMW87] we attach to
![]() $(S,\unicode[STIX]{x1D711})$
a certain smooth representation
$(S,\unicode[STIX]{x1D711})$
a certain smooth representation
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
of
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
of
![]() $G$
called a degenerate Whittaker model for
$G$
called a degenerate Whittaker model for
![]() $G$
.
$G$
.
Two classes of Whittaker pairs and the corresponding models will be of special interest to us. If
![]() $S$
is a neutral element for
$S$
is a neutral element for
![]() $f_{\unicode[STIX]{x1D711}}$
(see Definition 2.2.2 below), then we will say that
$f_{\unicode[STIX]{x1D711}}$
(see Definition 2.2.2 below), then we will say that
![]() $(S,\unicode[STIX]{x1D711})$
is a neutral pair and call
$(S,\unicode[STIX]{x1D711})$
is a neutral pair and call
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
a neutral model or a generalized model (see [Reference KawanakaKaw85, Reference Moeglin and WaldspurgerMW87, Reference YamashitaYam86, Reference Gomez and ZhuGZ14]). The second class consists of Whittaker pairs
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
a neutral model or a generalized model (see [Reference KawanakaKaw85, Reference Moeglin and WaldspurgerMW87, Reference YamashitaYam86, Reference Gomez and ZhuGZ14]). The second class consists of Whittaker pairs
![]() $(S,\unicode[STIX]{x1D711})$
where
$(S,\unicode[STIX]{x1D711})$
where
![]() $S$
is the neutral element of a principal
$S$
is the neutral element of a principal
![]() $\mathfrak{sl}_{2}$
-triple in
$\mathfrak{sl}_{2}$
-triple in
![]() $G$
; in this case
$G$
; in this case
![]() $f_{\unicode[STIX]{x1D711}}$
is necessarily a principal nilpotent element for a Levi subgroup of
$f_{\unicode[STIX]{x1D711}}$
is necessarily a principal nilpotent element for a Levi subgroup of
![]() $G$
, and we will say
$G$
, and we will say
![]() $(S,\unicode[STIX]{x1D711})$
is a PL pair, and
$(S,\unicode[STIX]{x1D711})$
is a PL pair, and
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
is a PL model or a principal degenerate model (see [Reference ZelevinskyZel80, Reference Moeglin and WaldspurgerMW87, Reference Bushnell and HenniartBH03, Reference Gourevitch and SahiGS13]).
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
is a PL model or a principal degenerate model (see [Reference ZelevinskyZel80, Reference Moeglin and WaldspurgerMW87, Reference Bushnell and HenniartBH03, Reference Gourevitch and SahiGS13]).
We will now sketch the definition of
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
, referring to § 2.5 below for more details. Let
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
, referring to § 2.5 below for more details. Let
![]() $\mathfrak{u}\subset \mathfrak{g}$
denote the sum of all eigenspaces of
$\mathfrak{u}\subset \mathfrak{g}$
denote the sum of all eigenspaces of
![]() $\text{ad}(S)$
with eigenvalues at least 1. Note that
$\text{ad}(S)$
with eigenvalues at least 1. Note that
![]() $\mathfrak{u}$
is a nilpotent subalgebra and let
$\mathfrak{u}$
is a nilpotent subalgebra and let
 $U:=\text{Exp}(\mathfrak{u})\subset G$
be the corresponding nilpotent subgroup. Fix an additive character of
$U:=\text{Exp}(\mathfrak{u})\subset G$
be the corresponding nilpotent subgroup. Fix an additive character of
![]() $\mathbb{F}$
. Suppose first that 1 is not an eigenvalue of
$\mathbb{F}$
. Suppose first that 1 is not an eigenvalue of
![]() $\text{ad}(S)$
. Then the restriction of
$\text{ad}(S)$
. Then the restriction of
![]() $\unicode[STIX]{x1D711}$
to
$\unicode[STIX]{x1D711}$
to
![]() $\mathfrak{u}$
is a character of
$\mathfrak{u}$
is a character of
![]() $\mathfrak{u}$
, which defines a character
$\mathfrak{u}$
, which defines a character
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
of
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
of
![]() $U$
. The degenerate Whittaker model is defined to be the Schwartz induction of this character:
$U$
. The degenerate Whittaker model is defined to be the Schwartz induction of this character:
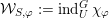 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}:=\text{ind}_{U}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. If 1 is an eigenvalue of
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}:=\text{ind}_{U}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. If 1 is an eigenvalue of
![]() $\text{ad}(S)$
, then consider the anti-symmetric form on
$\text{ad}(S)$
, then consider the anti-symmetric form on
![]() $\mathfrak{u}$
given by
$\mathfrak{u}$
given by
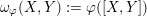 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}(X,Y):=\unicode[STIX]{x1D711}([X,Y])$
and let
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}(X,Y):=\unicode[STIX]{x1D711}([X,Y])$
and let
![]() $\mathfrak{n}$
denote the radical of this form. Let
$\mathfrak{n}$
denote the radical of this form. Let
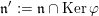 $\mathfrak{n}^{\prime }:=\mathfrak{n}\cap \text{Ker}\,\unicode[STIX]{x1D711}$
, and let
$\mathfrak{n}^{\prime }:=\mathfrak{n}\cap \text{Ker}\,\unicode[STIX]{x1D711}$
, and let
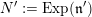 $N^{\prime }:=\text{Exp}(\mathfrak{n}^{\prime })$
. It is easy to show that
$N^{\prime }:=\text{Exp}(\mathfrak{n}^{\prime })$
. It is easy to show that
![]() $N^{\prime }$
is a normal subgroup of
$N^{\prime }$
is a normal subgroup of
![]() $U$
and
$U$
and
![]() $U/N^{\prime }$
is isomorphic to a (generalized) Heisenberg group, of which
$U/N^{\prime }$
is isomorphic to a (generalized) Heisenberg group, of which
![]() $\unicode[STIX]{x1D711}$
defines a central character
$\unicode[STIX]{x1D711}$
defines a central character
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. Let
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. Let
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
denote the oscillator representation of
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
denote the oscillator representation of
![]() $U/N^{\prime }$
with central character
$U/N^{\prime }$
with central character
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. Consider
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. Consider
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
as a representation of
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
as a representation of
![]() $U$
and define
$U$
and define
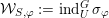 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}:=\text{ind}_{U}^{G}\,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
.
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}:=\text{ind}_{U}^{G}\,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
.
If
![]() $(S,\unicode[STIX]{x1D711})$
is a neutral pair, then the generalized Whittaker model
$(S,\unicode[STIX]{x1D711})$
is a neutral pair, then the generalized Whittaker model
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
does not depend on the choice of a neutral
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
does not depend on the choice of a neutral
![]() $S$
, and will thus be denoted
$S$
, and will thus be denoted
![]() ${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
. Since conjugate nilpotent elements give rise to isomorphic generalized Whittaker models, we will also use the notation
${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
. Since conjugate nilpotent elements give rise to isomorphic generalized Whittaker models, we will also use the notation
![]() ${\mathcal{W}}_{{\mathcal{O}}}$
for a nilpotent coadjoint orbit
${\mathcal{W}}_{{\mathcal{O}}}$
for a nilpotent coadjoint orbit
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
We denote by
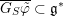 $\overline{G_{S}\tilde{\unicode[STIX]{x1D711}}}\subset \mathfrak{g}^{\ast }$
the closure of the orbit of
$\overline{G_{S}\tilde{\unicode[STIX]{x1D711}}}\subset \mathfrak{g}^{\ast }$
the closure of the orbit of
![]() $\tilde{\unicode[STIX]{x1D711}}$
under the coadjoint action of the centralizer of
$\tilde{\unicode[STIX]{x1D711}}$
under the coadjoint action of the centralizer of
![]() $S$
in
$S$
in
![]() $G$
.
$G$
.
Theorem A (See § 3).
Let
![]() $(S,\tilde{\unicode[STIX]{x1D711}})$
be a Whittaker pair and let
$(S,\tilde{\unicode[STIX]{x1D711}})$
be a Whittaker pair and let
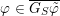 $\unicode[STIX]{x1D711}\in \overline{G_{S}\tilde{\unicode[STIX]{x1D711}}}$
. Then there is a
$\unicode[STIX]{x1D711}\in \overline{G_{S}\tilde{\unicode[STIX]{x1D711}}}$
. Then there is a
![]() $G$
-equivariant epimorphism of
$G$
-equivariant epimorphism of
![]() ${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
onto
${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
onto
![]() ${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}$
.
${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}$
.
In particular, taking
![]() $\tilde{\unicode[STIX]{x1D711}}=\unicode[STIX]{x1D711}$
we see that the generalized Whittaker model maps onto any degenerate Whittaker model corresponding to the same
$\tilde{\unicode[STIX]{x1D711}}=\unicode[STIX]{x1D711}$
we see that the generalized Whittaker model maps onto any degenerate Whittaker model corresponding to the same
![]() $\unicode[STIX]{x1D711}$
. In fact, we prove a more general result (Theorem 3.0.1) on epimorphisms between pairs of degenerate Whittaker models, which enables one to define a preorder on the pairs
$\unicode[STIX]{x1D711}$
. In fact, we prove a more general result (Theorem 3.0.1) on epimorphisms between pairs of degenerate Whittaker models, which enables one to define a preorder on the pairs
![]() $(S,\unicode[STIX]{x1D711})$
. If we fix
$(S,\unicode[STIX]{x1D711})$
. If we fix
![]() $f_{\unicode[STIX]{x1D711}}$
to be a regular nilpotent element for a Levi subgroup of
$f_{\unicode[STIX]{x1D711}}$
to be a regular nilpotent element for a Levi subgroup of
![]() $G$
, then the minimal elements under this preorder are the PL Whittaker pairs (see § 3.3). The corresponding principal degenerate Whittaker models are inductions of (possibly degenerate) characters of the nilradicals of minimal parabolic subgroups.
$G$
, then the minimal elements under this preorder are the PL Whittaker pairs (see § 3.3). The corresponding principal degenerate Whittaker models are inductions of (possibly degenerate) characters of the nilradicals of minimal parabolic subgroups.
The above results have applications to the study of Whittaker functionals on representations of
![]() $G$
. Following [Reference Gomez and ZhuGZ14] we briefly recall the necessary background.
$G$
. Following [Reference Gomez and ZhuGZ14] we briefly recall the necessary background.
Let
![]() ${\mathcal{M}}(G)$
denote the category of smooth admissibleFootnote
1
(finitely generated) representations of
${\mathcal{M}}(G)$
denote the category of smooth admissibleFootnote
1
(finitely generated) representations of
![]() $G$
(see [Reference Bernstein and ZelevinskyBZ76, Reference CasselmanCas89, Reference WallachWal92]). For
$G$
(see [Reference Bernstein and ZelevinskyBZ76, Reference CasselmanCas89, Reference WallachWal92]). For
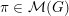 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
and a nilpotent orbit
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
and a nilpotent orbit
![]() ${\mathcal{O}}\subset \mathfrak{g}$
denote
${\mathcal{O}}\subset \mathfrak{g}$
denote
 $$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B}):=\text{Hom}_{G}({\mathcal{W}}_{{\mathcal{O}}},\unicode[STIX]{x1D70B}^{\ast }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B}):=\text{Hom}_{G}({\mathcal{W}}_{{\mathcal{O}}},\unicode[STIX]{x1D70B}^{\ast }).\end{eqnarray}$$
The study of Whittaker and generalized Whittaker models for representations of reductive groups over local fields evolved in connection with the theory of automorphic forms (via their Fourier coefficients), and has found important applications in both areas. See for example [Reference ShalikaSha74, Reference Novodvorskii and Piatetski-ShapiroNP73, Reference KostantKos78, Reference KawanakaKaw85, Reference YamashitaYam86, Reference WallachWal88, Reference GinzburgGin06, Reference JiangJia07, Reference Ginzburg, Rallis and SoudryGRS11]. From the point of view of representation theory, the space of generalized Whittaker models may be viewed as one kind of nilpotent invariant associated to smooth representations. Another important invariant is the wave-front cycle:
 $$\begin{eqnarray}\operatorname{WFC}(\unicode[STIX]{x1D70B})=\mathop{\sum }_{\stackrel{{\mathcal{O}}\subset \mathfrak{g}^{\ast }}{\text{nilpotent}}}c_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})[{\mathcal{O}}],\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{WFC}(\unicode[STIX]{x1D70B})=\mathop{\sum }_{\stackrel{{\mathcal{O}}\subset \mathfrak{g}^{\ast }}{\text{nilpotent}}}c_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})[{\mathcal{O}}],\end{eqnarray}$$
defined by Harish-Chandra in the non-archimedean case and by Howe and Barbasch–Vogan in the archimedean case ([Reference HoweHow81, Reference Barbasch and VoganBV80]; see also [Reference RossmannRos95, Reference Schmid and VilonenSV00]). Recently, the behavior of the wave-front set and the generalized Whittaker models under
![]() $\unicode[STIX]{x1D703}$
-correspondence was studied in [Reference Gomez and ZhuGZ14, Reference Loke and MaLM15b].
$\unicode[STIX]{x1D703}$
-correspondence was studied in [Reference Gomez and ZhuGZ14, Reference Loke and MaLM15b].
For
![]() $\mathbb{F}$
non-archimedean, Mœglin and Waldspurger [Reference Moeglin and WaldspurgerMW87] have established that
$\mathbb{F}$
non-archimedean, Mœglin and Waldspurger [Reference Moeglin and WaldspurgerMW87] have established that
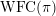 $\operatorname{WFC}(\unicode[STIX]{x1D70B})$
completely controls the spaces of generalized Whittaker models of interest, namely, the set of maximal orbits in
$\operatorname{WFC}(\unicode[STIX]{x1D70B})$
completely controls the spaces of generalized Whittaker models of interest, namely, the set of maximal orbits in
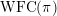 $\operatorname{WFC}(\unicode[STIX]{x1D70B})$
coincides with the set of maximal orbits such that
$\operatorname{WFC}(\unicode[STIX]{x1D70B})$
coincides with the set of maximal orbits such that
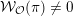 ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
, and for any orbit
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
, and for any orbit
![]() ${\mathcal{O}}$
in this set we have
${\mathcal{O}}$
in this set we have
 $$\begin{eqnarray}c_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})=\dim {\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B}).\end{eqnarray}$$
$$\begin{eqnarray}c_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})=\dim {\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B}).\end{eqnarray}$$
In [Reference Moeglin and WaldspurgerMW87] it is assumed that the residue characteristic is odd. This assumption was recently removed in [Reference VarmaVar14]. In [Reference MoeglinMoe96], the main result of [Reference Moeglin and WaldspurgerMW87] is used in order to prove that for classical groups, the maximal orbits in the wave-front set of a tempered representation are distinguished, and the maximal orbits in the wave-front set of any admissible representation are special. The latter was recently generalized in [Reference Jiang, Liu and SavinJLS14]. Partial analogs of these results hold also for archimedean
![]() $\mathbb{F}$
, see [Reference HarrisHar12] for the former and [Reference Barbasch and VoganBV82, Reference Barbasch and VoganBV83, Reference JosephJos80] for the latter.
$\mathbb{F}$
, see [Reference HarrisHar12] for the former and [Reference Barbasch and VoganBV82, Reference Barbasch and VoganBV83, Reference JosephJos80] for the latter.
For archimedean
![]() $\mathbb{F}$
, the correspondence between the wave-front set and non-vanishing of degenerate Whittaker models is not yet (fully) understood, except for several special cases including the representations with the largest Gelfand–Kirillov dimension [Reference VoganVog78, Reference MatumotoMat92] and unitary highest weight modules [Reference YamashitaYam01]. For the latter, the wave-front set was computed earlier in [Reference PrzebindaPrz91]. In [Reference MatumotoMat87], it is shown in full generality that every orbit
$\mathbb{F}$
, the correspondence between the wave-front set and non-vanishing of degenerate Whittaker models is not yet (fully) understood, except for several special cases including the representations with the largest Gelfand–Kirillov dimension [Reference VoganVog78, Reference MatumotoMat92] and unitary highest weight modules [Reference YamashitaYam01]. For the latter, the wave-front set was computed earlier in [Reference PrzebindaPrz91]. In [Reference MatumotoMat87], it is shown in full generality that every orbit
![]() ${\mathcal{O}}$
with
${\mathcal{O}}$
with
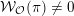 ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
lies in the Zariski closure of some orbit in
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
lies in the Zariski closure of some orbit in
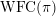 $\operatorname{WFC}(\unicode[STIX]{x1D70B})$
. The paper [Reference Gourevitch and SahiGS15] proves an expected existence of non-zero maps from principal degenerate Whittaker models to admissible representations, and by Proposition 3.3.4 below, any other degenerate Whittaker model corresponding to the same orbit is mapped onto a principal degenerate Whittaker model. Let
$\operatorname{WFC}(\unicode[STIX]{x1D70B})$
. The paper [Reference Gourevitch and SahiGS15] proves an expected existence of non-zero maps from principal degenerate Whittaker models to admissible representations, and by Proposition 3.3.4 below, any other degenerate Whittaker model corresponding to the same orbit is mapped onto a principal degenerate Whittaker model. Let
![]() $\operatorname{WF}(\unicode[STIX]{x1D70B})$
denote the closure in the local field topology of the union of all of the orbits in
$\operatorname{WF}(\unicode[STIX]{x1D70B})$
denote the closure in the local field topology of the union of all of the orbits in
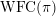 $\operatorname{WFC}(\unicode[STIX]{x1D70B})$
. In § 3.3 we review the results of [Reference MatumotoMat87, Reference Gourevitch and SahiGS15] and deduce, using Theorem A, the following theorem.
$\operatorname{WFC}(\unicode[STIX]{x1D70B})$
. In § 3.3 we review the results of [Reference MatumotoMat87, Reference Gourevitch and SahiGS15] and deduce, using Theorem A, the following theorem.
Theorem B (§ 3.3).
Let
![]() $G$
be a complex reductive group and let
$G$
be a complex reductive group and let
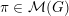 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
. Let
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
. Let
![]() $(S,\unicode[STIX]{x1D711})$
be a Whittaker pair such that
$(S,\unicode[STIX]{x1D711})$
be a Whittaker pair such that
![]() $\unicode[STIX]{x1D711}$
is given by Killing form pairing with a principal nilpotent element of the Lie algebra of a Levi subgroup of
$\unicode[STIX]{x1D711}$
is given by Killing form pairing with a principal nilpotent element of the Lie algebra of a Levi subgroup of
![]() $G$
. Then
$G$
. Then
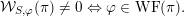 $$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0\Leftrightarrow \unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0\Leftrightarrow \unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B}).\end{eqnarray}$$
If
![]() $G$
is classical, then the set
$G$
is classical, then the set
![]() $\operatorname{WF}(\unicode[STIX]{x1D70B})$
is uniquely determined by its intersection with the set of ‘principal Levi’ nilpotents
$\operatorname{WF}(\unicode[STIX]{x1D70B})$
is uniquely determined by its intersection with the set of ‘principal Levi’ nilpotents
![]() $\unicode[STIX]{x1D711}$
; see [Reference Gourevitch and SahiGS15, Theorem D]. A result related to Theorem B is proved by Matumoto in [Reference MatumotoMat90]. Namely, let
$\unicode[STIX]{x1D711}$
; see [Reference Gourevitch and SahiGS15, Theorem D]. A result related to Theorem B is proved by Matumoto in [Reference MatumotoMat90]. Namely, let
![]() $G$
be a complex reductive group and let
$G$
be a complex reductive group and let
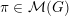 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
have regular infinitesimal character. Let
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
have regular infinitesimal character. Let
![]() $(S,\unicode[STIX]{x1D711})$
be a Whittaker pair and assume that the orbit of
$(S,\unicode[STIX]{x1D711})$
be a Whittaker pair and assume that the orbit of
![]() $\unicode[STIX]{x1D711}$
is dense in
$\unicode[STIX]{x1D711}$
is dense in
![]() $\operatorname{WF}(\unicode[STIX]{x1D70B})$
, and also that it contains a dense subset of the nilradical of the parabolic subgroup defined by
$\operatorname{WF}(\unicode[STIX]{x1D70B})$
, and also that it contains a dense subset of the nilradical of the parabolic subgroup defined by
![]() $S$
. Then
$S$
. Then
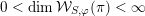 $0<\dim {\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})<\infty$
. Matumoto also proves the vanishing of the corresponding higher homology groups.
$0<\dim {\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})<\infty$
. Matumoto also proves the vanishing of the corresponding higher homology groups.
For
![]() $\mathbb{F}=\mathbb{R}$
a weaker version of Theorem B holds, see Corollary 3.3.7 below.
$\mathbb{F}=\mathbb{R}$
a weaker version of Theorem B holds, see Corollary 3.3.7 below.
In § 5 we give choice-free definitions of degenerate Whittaker models. These definitions use the Deligne filtration instead of the Jacobson–Morozov theorem and thus might be suitable for local fields of positive characteristic.
In the global case, instead of degenerate Whittaker models one considers explicit functionals on automorphic representations defined by integration against a character of a nilpotent subgroup. Such functionals are called Whittaker–Fourier coefficients and denoted
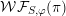 ${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
. In § 6 we give the definitions and explain how to adapt our arguments to the global case and deduce the following theorem.
${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
. In § 6 we give the definitions and explain how to adapt our arguments to the global case and deduce the following theorem.
Theorem C (See § 6).
Let
![]() $K$
be a number field, let
$K$
be a number field, let
![]() $G$
be the group of adelic points of a reductive group defined over
$G$
be the group of adelic points of a reductive group defined over
![]() $K$
and
$K$
and
![]() $\mathfrak{g}$
be its Lie algebra. Let
$\mathfrak{g}$
be its Lie algebra. Let
![]() $\unicode[STIX]{x1D70B}$
be an automorphic representation of
$\unicode[STIX]{x1D70B}$
be an automorphic representation of
![]() $G$
. Let
$G$
. Let
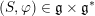 $(S,\unicode[STIX]{x1D711})\in \mathfrak{g}\times \mathfrak{g}^{\ast }$
be a Whittaker pair. Suppose that
$(S,\unicode[STIX]{x1D711})\in \mathfrak{g}\times \mathfrak{g}^{\ast }$
be a Whittaker pair. Suppose that
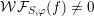 ${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(f)\neq 0$
for some
${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(f)\neq 0$
for some
![]() $f\in \unicode[STIX]{x1D70B}$
. Then
$f\in \unicode[STIX]{x1D70B}$
. Then
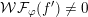 ${\mathcal{W}}{\mathcal{F}}_{\unicode[STIX]{x1D711}}(f^{\prime })\neq 0$
for some
${\mathcal{W}}{\mathcal{F}}_{\unicode[STIX]{x1D711}}(f^{\prime })\neq 0$
for some
![]() $f^{\prime }\in \unicode[STIX]{x1D70B}$
.
$f^{\prime }\in \unicode[STIX]{x1D70B}$
.
1.2 Further results for
 $\text{GL}_{n}(\mathbb{F})$
$\text{GL}_{n}(\mathbb{F})$
For
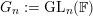 $G_{n}:=\text{GL}_{n}(\mathbb{F})$
we show that Theorem A allows one to compare degenerate Whittaker models corresponding to any nilpotent orbits
$G_{n}:=\text{GL}_{n}(\mathbb{F})$
we show that Theorem A allows one to compare degenerate Whittaker models corresponding to any nilpotent orbits
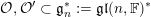 ${\mathcal{O}},{\mathcal{O}}^{\prime }\subset \mathfrak{g}_{n}^{\ast }:=\mathfrak{gl}(n,\mathbb{F})^{\ast }$
such that
${\mathcal{O}},{\mathcal{O}}^{\prime }\subset \mathfrak{g}_{n}^{\ast }:=\mathfrak{gl}(n,\mathbb{F})^{\ast }$
such that
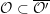 ${\mathcal{O}}\subset \overline{{\mathcal{O}}^{\prime }}$
. To that end we prove the following geometric theorem.
${\mathcal{O}}\subset \overline{{\mathcal{O}}^{\prime }}$
. To that end we prove the following geometric theorem.
Theorem D (§ 4.2).
Let
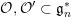 ${\mathcal{O}},{\mathcal{O}}^{\prime }\subset \mathfrak{g}_{n}^{\ast }$
be nilpotent coadjoint orbits with
${\mathcal{O}},{\mathcal{O}}^{\prime }\subset \mathfrak{g}_{n}^{\ast }$
be nilpotent coadjoint orbits with
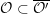 ${\mathcal{O}}\subset \overline{{\mathcal{O}}^{\prime }}$
. Then there exists a Whittaker pair
${\mathcal{O}}\subset \overline{{\mathcal{O}}^{\prime }}$
. Then there exists a Whittaker pair
![]() $(S,\tilde{\unicode[STIX]{x1D711}})$
such that
$(S,\tilde{\unicode[STIX]{x1D711}})$
such that
![]() $\tilde{\unicode[STIX]{x1D711}}\in {\mathcal{O}}^{\prime }$
and
$\tilde{\unicode[STIX]{x1D711}}\in {\mathcal{O}}^{\prime }$
and
![]() ${\mathcal{O}}$
intersects
${\mathcal{O}}$
intersects
![]() $\overline{G_{S}\tilde{\unicode[STIX]{x1D711}}}$
. Moreover,
$\overline{G_{S}\tilde{\unicode[STIX]{x1D711}}}$
. Moreover,
![]() $S$
can be chosen to be diagonal with integer eigenvalues and
$S$
can be chosen to be diagonal with integer eigenvalues and
![]() $\tilde{\unicode[STIX]{x1D711}}$
can be chosen to be given by the trace pairing with a matrix in Jordan form.
$\tilde{\unicode[STIX]{x1D711}}$
can be chosen to be given by the trace pairing with a matrix in Jordan form.
Remark 1.2.1. An analogous statement holds for some pairs of nilpotent orbits
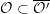 ${\mathcal{O}}\subset \overline{{\mathcal{O}}^{\prime }}$
in other classical groups (see Remark 4.3.2 below), but not in general. Indeed, it can be shown that if
${\mathcal{O}}\subset \overline{{\mathcal{O}}^{\prime }}$
in other classical groups (see Remark 4.3.2 below), but not in general. Indeed, it can be shown that if
![]() $\overline{G_{S}\tilde{\unicode[STIX]{x1D711}}}$
intersects a distinguished orbit
$\overline{G_{S}\tilde{\unicode[STIX]{x1D711}}}$
intersects a distinguished orbit
![]() ${\mathcal{O}}$
, then
${\mathcal{O}}$
, then
![]() ${\mathcal{O}}={\mathcal{O}}^{\prime }$
.
${\mathcal{O}}={\mathcal{O}}^{\prime }$
.
Using Theorem B [Reference MatumotoMat87] and Corollary 3.3.7 for archimedean
![]() $\mathbb{F}$
, and Theorems A and D, together with the results of [Reference Moeglin and WaldspurgerMW87, Reference VarmaVar14] for non-archimedean
$\mathbb{F}$
, and Theorems A and D, together with the results of [Reference Moeglin and WaldspurgerMW87, Reference VarmaVar14] for non-archimedean
![]() $\mathbb{F}$
we deduce the following theorem.
$\mathbb{F}$
we deduce the following theorem.
Theorem E (§ 4.3).
Let
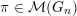 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
. Let
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
. Let
![]() ${\mathcal{O}}\subset \mathfrak{g}_{n}^{\ast }$
be a nilpotent orbit. Then we have
${\mathcal{O}}\subset \mathfrak{g}_{n}^{\ast }$
be a nilpotent orbit. Then we have
 $$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0\Leftrightarrow {\mathcal{O}}\subset \operatorname{WF}(\unicode[STIX]{x1D70B}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0\Leftrightarrow {\mathcal{O}}\subset \operatorname{WF}(\unicode[STIX]{x1D70B}).\end{eqnarray}$$
Remark 1.2.2. It would be interesting to know to what extent this theorem holds for other reductive groups. For archimedean
![]() $\mathbb{F}$
, Theorem B and Corollary 3.3.7 provide a partial extension. In the non-archimedean case, the failure of Theorem D for general groups, as noted in Remark 1.2.1, represents the main obstacle for extending our approach.
$\mathbb{F}$
, Theorem B and Corollary 3.3.7 provide a partial extension. In the non-archimedean case, the failure of Theorem D for general groups, as noted in Remark 1.2.1, represents the main obstacle for extending our approach.
In § 4.4 we give a precise description of the generalized Whittaker spaces in terms of certain functors
![]() $E^{k}$
introduced in [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b] in connection with the generalization of the theory of Bernstein–Zelevinsky derivatives to the archimedean setting. We will also use related functors
$E^{k}$
introduced in [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b] in connection with the generalization of the theory of Bernstein–Zelevinsky derivatives to the archimedean setting. We will also use related functors
![]() $I^{k}$
that go in the other direction. We refer to § 4.4 below for the precise definitions of both functors.
$I^{k}$
that go in the other direction. We refer to § 4.4 below for the precise definitions of both functors.
Theorem F (§ 4.4).
Let
 $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{k})$
be a partition of
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{k})$
be a partition of
![]() $n$
and
$n$
and
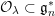 ${\mathcal{O}}_{\unicode[STIX]{x1D706}}\subset \mathfrak{g}_{n}^{\ast }$
be the corresponding nilpotent orbit. Then
${\mathcal{O}}_{\unicode[STIX]{x1D706}}\subset \mathfrak{g}_{n}^{\ast }$
be the corresponding nilpotent orbit. Then
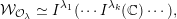 $$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}\simeq I^{\unicode[STIX]{x1D706}_{1}}(\cdots I^{\unicode[STIX]{x1D706}_{k}}(\mathbb{C})\cdots \,),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}\simeq I^{\unicode[STIX]{x1D706}_{1}}(\cdots I^{\unicode[STIX]{x1D706}_{k}}(\mathbb{C})\cdots \,),\end{eqnarray}$$
where
![]() $\mathbb{C}$
denotes the one-dimensional representation of the trivial group
$\mathbb{C}$
denotes the one-dimensional representation of the trivial group
![]() $G_{0}$
, and for
$G_{0}$
, and for
 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
we have
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
we have
 $$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D70B})\simeq (E^{\unicode[STIX]{x1D706}_{k}}(\cdots E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})\cdots \,))^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D70B})\simeq (E^{\unicode[STIX]{x1D706}_{k}}(\cdots E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})\cdots \,))^{\ast }.\end{eqnarray}$$
Let
![]() ${\mathcal{O}}\subset \mathfrak{g}_{n}^{\ast }$
be a nilpotent orbit. Let
${\mathcal{O}}\subset \mathfrak{g}_{n}^{\ast }$
be a nilpotent orbit. Let
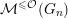 ${\mathcal{M}}^{{\leqslant}{\mathcal{O}}}(G_{n})$
denote the Serre subcategory of
${\mathcal{M}}^{{\leqslant}{\mathcal{O}}}(G_{n})$
denote the Serre subcategory of
![]() ${\mathcal{M}}(G_{n})$
consisting of representations with wave-front set inside the closure of
${\mathcal{M}}(G_{n})$
consisting of representations with wave-front set inside the closure of
![]() ${\mathcal{O}}$
and let
${\mathcal{O}}$
and let
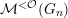 ${\mathcal{M}}^{{<}{\mathcal{O}}}(G_{n})$
denote the Serre subcategory of
${\mathcal{M}}^{{<}{\mathcal{O}}}(G_{n})$
denote the Serre subcategory of
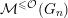 ${\mathcal{M}}^{{\leqslant}{\mathcal{O}}}(G_{n})$
consisting of representations with wave-front set not containing
${\mathcal{M}}^{{\leqslant}{\mathcal{O}}}(G_{n})$
consisting of representations with wave-front set not containing
![]() ${\mathcal{O}}$
. Let
${\mathcal{O}}$
. Let
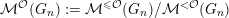 ${\mathcal{M}}^{{\mathcal{O}}}(G_{n}):={\mathcal{M}}^{{\leqslant}{\mathcal{O}}}(G_{n})/{\mathcal{M}}^{{<}{\mathcal{O}}}(G_{n})$
denote the quotient category.
${\mathcal{M}}^{{\mathcal{O}}}(G_{n}):={\mathcal{M}}^{{\leqslant}{\mathcal{O}}}(G_{n})/{\mathcal{M}}^{{<}{\mathcal{O}}}(G_{n})$
denote the quotient category.
Using the main results of [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b, Reference Gourevitch and SahiGS13, Reference Gourevitch and SahiGS15] we obtain the following corollary.
Corollary G (§ 4.5).
![]() $~\text{(i)}$
The functor
$~\text{(i)}$
The functor
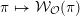 $\unicode[STIX]{x1D70B}\mapsto {\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
defines an exact faithful functor from
$\unicode[STIX]{x1D70B}\mapsto {\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
defines an exact faithful functor from
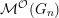 ${\mathcal{M}}^{{\mathcal{O}}}(G_{n})$
to the category of finite-dimensional vector spaces.
${\mathcal{M}}^{{\mathcal{O}}}(G_{n})$
to the category of finite-dimensional vector spaces.
![]() $\text{(ii)}$
If
$\text{(ii)}$
If
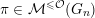 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}^{{\leqslant}{\mathcal{O}}}(G_{n})$
is an irreducible unitarizable representation, or a monomial representation, and
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}^{{\leqslant}{\mathcal{O}}}(G_{n})$
is an irreducible unitarizable representation, or a monomial representation, and
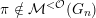 $\unicode[STIX]{x1D70B}\notin {\mathcal{M}}^{{<}{\mathcal{O}}}(G_{n})$
then
$\unicode[STIX]{x1D70B}\notin {\mathcal{M}}^{{<}{\mathcal{O}}}(G_{n})$
then
![]() ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
is one-dimensional.
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
is one-dimensional.
This corollary is new only in the archimedean case, since over
![]() $p$
-adic fields exactness is well-known and finiteness of dimension is shown in [Reference Moeglin and WaldspurgerMW87]. It is also shown in [Reference Moeglin and WaldspurgerMW87] that
$p$
-adic fields exactness is well-known and finiteness of dimension is shown in [Reference Moeglin and WaldspurgerMW87]. It is also shown in [Reference Moeglin and WaldspurgerMW87] that
![]() ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
is one-dimensional for all irreducible
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
is one-dimensional for all irreducible
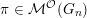 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}^{{\mathcal{O}}}(G_{n})$
. Over archimedean fields,
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}^{{\mathcal{O}}}(G_{n})$
. Over archimedean fields,
![]() ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
is clearly not one-dimensional for any irreducible
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
is clearly not one-dimensional for any irreducible
![]() $\unicode[STIX]{x1D70B}$
of finite dimension bigger than one.
$\unicode[STIX]{x1D70B}$
of finite dimension bigger than one.
Let us also comment that for any irreducible
 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
,
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
,
![]() $\operatorname{WF}(\unicode[STIX]{x1D70B})$
is the closure of a single nilpotent orbit. Over archimedean fields this follows from [Reference Borho and BrylinskiBB82, Reference JosephJos85] and over non-archimedean fields this is proven in [Reference Moeglin and WaldspurgerMW87]. More generally, it follows from [Reference JosephJos85] that for any real reductive group
$\operatorname{WF}(\unicode[STIX]{x1D70B})$
is the closure of a single nilpotent orbit. Over archimedean fields this follows from [Reference Borho and BrylinskiBB82, Reference JosephJos85] and over non-archimedean fields this is proven in [Reference Moeglin and WaldspurgerMW87]. More generally, it follows from [Reference JosephJos85] that for any real reductive group
![]() $G$
and any irreducible
$G$
and any irreducible
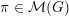 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
, all of the maximal orbits in
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
, all of the maximal orbits in
![]() $\operatorname{WF}(\unicode[STIX]{x1D70B})$
lie in a single complex nilpotent orbit. An analogous statement is conjectured over
$\operatorname{WF}(\unicode[STIX]{x1D70B})$
lie in a single complex nilpotent orbit. An analogous statement is conjectured over
![]() $p$
-adic fields but not proven yet.
$p$
-adic fields but not proven yet.
We conjecture that the functor
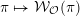 $\unicode[STIX]{x1D70B}\mapsto {\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
is exact for all reductive groups, and we hope to prove this in the future, generalizing the technique of [Reference Aizenbud, Gourevitch and SahiAGS15b].
$\unicode[STIX]{x1D70B}\mapsto {\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
is exact for all reductive groups, and we hope to prove this in the future, generalizing the technique of [Reference Aizenbud, Gourevitch and SahiAGS15b].
1.3 The structure of our proofs
Let us first describe the idea of the proof of Theorem A in the case
![]() $\unicode[STIX]{x1D711}=\tilde{\unicode[STIX]{x1D711}}$
. We first show that
$\unicode[STIX]{x1D711}=\tilde{\unicode[STIX]{x1D711}}$
. We first show that
![]() $S$
can be presented as
$S$
can be presented as
![]() $h+Z$
, where
$h+Z$
, where
![]() $h$
is a neutral element for
$h$
is a neutral element for
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $Z$
commutes with
$Z$
commutes with
![]() $h$
and
$h$
and
![]() $\unicode[STIX]{x1D711}$
. Then we consider a deformation
$\unicode[STIX]{x1D711}$
. Then we consider a deformation
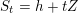 $S_{t}=h+tZ$
, and denote by
$S_{t}=h+tZ$
, and denote by
![]() $\mathfrak{u}_{t}$
the sum of eigenspaces of
$\mathfrak{u}_{t}$
the sum of eigenspaces of
![]() $\text{ad}(S_{t})$
with eigenvalues at least 1. We call a rational number
$\text{ad}(S_{t})$
with eigenvalues at least 1. We call a rational number
 $0<t<1$
regular if
$0<t<1$
regular if
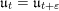 $\mathfrak{u}_{t}=\mathfrak{u}_{t+\unicode[STIX]{x1D700}}$
for any small enough rational
$\mathfrak{u}_{t}=\mathfrak{u}_{t+\unicode[STIX]{x1D700}}$
for any small enough rational
![]() $\unicode[STIX]{x1D700}$
, and critical otherwise. Note that there are finitely many critical numbers, and denote them by
$\unicode[STIX]{x1D700}$
, and critical otherwise. Note that there are finitely many critical numbers, and denote them by
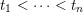 $t_{1}<\cdots <t_{n}$
. Denote also
$t_{1}<\cdots <t_{n}$
. Denote also
![]() $t_{0}:=0$
and
$t_{0}:=0$
and
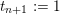 $t_{n+1}:=1$
. For each
$t_{n+1}:=1$
. For each
![]() $t$
we define two subalgebras
$t$
we define two subalgebras
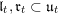 $\mathfrak{l}_{t},\mathfrak{r}_{t}\subset \mathfrak{u}_{t}$
. Both
$\mathfrak{l}_{t},\mathfrak{r}_{t}\subset \mathfrak{u}_{t}$
. Both
![]() $\mathfrak{l}_{t}$
and
$\mathfrak{l}_{t}$
and
![]() $\mathfrak{r}_{t}$
are maximal isotropic subspaces with respect to the form
$\mathfrak{r}_{t}$
are maximal isotropic subspaces with respect to the form
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}$
,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}$
,
![]() $\mathfrak{r}_{t}$
contains all of the eigenspaces of
$\mathfrak{r}_{t}$
contains all of the eigenspaces of
![]() $Z$
in
$Z$
in
![]() $\mathfrak{u}_{t}$
with positive eigenvalues and
$\mathfrak{u}_{t}$
with positive eigenvalues and
![]() $\mathfrak{l}_{t}$
contains all of the eigenspaces with negative eigenvalues. Note that the restrictions of
$\mathfrak{l}_{t}$
contains all of the eigenspaces with negative eigenvalues. Note that the restrictions of
![]() $\unicode[STIX]{x1D711}$
to
$\unicode[STIX]{x1D711}$
to
![]() $\mathfrak{l}_{t}$
and
$\mathfrak{l}_{t}$
and
![]() $\mathfrak{r}_{t}$
define characters of these subalgebras. Let
$\mathfrak{r}_{t}$
define characters of these subalgebras. Let
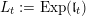 $L_{t}:=\text{Exp}(\mathfrak{l}_{t})$
and
$L_{t}:=\text{Exp}(\mathfrak{l}_{t})$
and
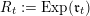 $R_{t}:=\text{Exp}(\mathfrak{r}_{t})$
denote the corresponding subgroups and
$R_{t}:=\text{Exp}(\mathfrak{r}_{t})$
denote the corresponding subgroups and
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
denote their characters defined by
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
denote their characters defined by
![]() $\unicode[STIX]{x1D711}$
. The Stone–von Neumann theorem implies
$\unicode[STIX]{x1D711}$
. The Stone–von Neumann theorem implies
 $$\begin{eqnarray}{\mathcal{W}}_{S_{t},\unicode[STIX]{x1D711}}\simeq \text{ind}_{L_{t}}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})\simeq \text{ind}_{R_{t}}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{S_{t},\unicode[STIX]{x1D711}}\simeq \text{ind}_{L_{t}}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})\simeq \text{ind}_{R_{t}}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}).\end{eqnarray}$$
We show that for any
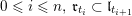 $0\leqslant i\leqslant n,\,\mathfrak{r}_{t_{i}}\subset \mathfrak{l}_{t_{i+1}}$
. This gives a natural epimorphism
$0\leqslant i\leqslant n,\,\mathfrak{r}_{t_{i}}\subset \mathfrak{l}_{t_{i+1}}$
. This gives a natural epimorphism
 $$\begin{eqnarray}{\mathcal{W}}_{S_{t_{i}},\unicode[STIX]{x1D711}}\simeq \text{ind}_{L_{t_{i}}}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})\,{\twoheadrightarrow}\,\text{ind}_{R_{t_{i}}}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})\simeq {\mathcal{W}}_{S_{t_{i+1}},\unicode[STIX]{x1D711}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{S_{t_{i}},\unicode[STIX]{x1D711}}\simeq \text{ind}_{L_{t_{i}}}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})\,{\twoheadrightarrow}\,\text{ind}_{R_{t_{i}}}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})\simeq {\mathcal{W}}_{S_{t_{i+1}},\unicode[STIX]{x1D711}}.\end{eqnarray}$$
Altogether, we get
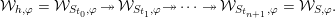 $$\begin{eqnarray}{\mathcal{W}}_{h,\unicode[STIX]{x1D711}}={\mathcal{W}}_{S_{t_{0}},\unicode[STIX]{x1D711}}\,{\twoheadrightarrow}\,{\mathcal{W}}_{S_{t_{1}},\unicode[STIX]{x1D711}}{\twoheadrightarrow}\cdots \,{\twoheadrightarrow}\,{\mathcal{W}}_{S_{t_{n+1}},\unicode[STIX]{x1D711}}={\mathcal{W}}_{S,\unicode[STIX]{x1D711}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{h,\unicode[STIX]{x1D711}}={\mathcal{W}}_{S_{t_{0}},\unicode[STIX]{x1D711}}\,{\twoheadrightarrow}\,{\mathcal{W}}_{S_{t_{1}},\unicode[STIX]{x1D711}}{\twoheadrightarrow}\cdots \,{\twoheadrightarrow}\,{\mathcal{W}}_{S_{t_{n+1}},\unicode[STIX]{x1D711}}={\mathcal{W}}_{S,\unicode[STIX]{x1D711}}.\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D711}\neq \tilde{\unicode[STIX]{x1D711}}$
, we identify
$\unicode[STIX]{x1D711}\neq \tilde{\unicode[STIX]{x1D711}}$
, we identify
![]() $\mathfrak{g}\simeq \mathfrak{g}^{\ast }$
using a non-degenerate invariant form and complete
$\mathfrak{g}\simeq \mathfrak{g}^{\ast }$
using a non-degenerate invariant form and complete
![]() $\unicode[STIX]{x1D711}$
to an
$\unicode[STIX]{x1D711}$
to an
![]() $sl_{2}$
-triple
$sl_{2}$
-triple
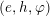 $(e,h,\unicode[STIX]{x1D711})$
such that
$(e,h,\unicode[STIX]{x1D711})$
such that
![]() $h$
commutes with
$h$
commutes with
![]() $S$
. Then we show, using the Slodowy slice, that the conditions imply that
$S$
. Then we show, using the Slodowy slice, that the conditions imply that
![]() $\tilde{\unicode[STIX]{x1D711}}$
is conjugate under
$\tilde{\unicode[STIX]{x1D711}}$
is conjugate under
![]() $G_{S}$
to
$G_{S}$
to
![]() $\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }$
with
$\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }$
with
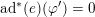 $\text{ad}^{\ast }(e)(\unicode[STIX]{x1D711}^{\prime })=0$
. We finish the proof by a deformation argument similar to the case
$\text{ad}^{\ast }(e)(\unicode[STIX]{x1D711}^{\prime })=0$
. We finish the proof by a deformation argument similar to the case
![]() $\unicode[STIX]{x1D711}=\tilde{\unicode[STIX]{x1D711}}$
.
$\unicode[STIX]{x1D711}=\tilde{\unicode[STIX]{x1D711}}$
.
For Theorem B, the implication
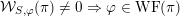 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0\Rightarrow \unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})$
follows from [Reference MatumotoMat87]. To prove the other direction, we show that
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0\Rightarrow \unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})$
follows from [Reference MatumotoMat87]. To prove the other direction, we show that
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
maps onto some principal degenerate Whittaker model
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
maps onto some principal degenerate Whittaker model
![]() ${\mathcal{W}}_{\tilde{S},\unicode[STIX]{x1D711}}$
. Thus the theorem follows from the non-vanishing of
${\mathcal{W}}_{\tilde{S},\unicode[STIX]{x1D711}}$
. Thus the theorem follows from the non-vanishing of
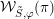 ${\mathcal{W}}_{\tilde{S},\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
(under the condition
${\mathcal{W}}_{\tilde{S},\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
(under the condition
 $\unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})$
), which was shown in [Reference Gourevitch and SahiGS15]. The same argument gives Corollary 3.3.7: an analogous statement for quasisplit real reductive groups.
$\unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})$
), which was shown in [Reference Gourevitch and SahiGS15]. The same argument gives Corollary 3.3.7: an analogous statement for quasisplit real reductive groups.
For the proof of Theorem D we identify
![]() $\mathfrak{g}_{n}^{\ast }$
with
$\mathfrak{g}_{n}^{\ast }$
with
![]() $\mathfrak{g}_{n}$
using the trace form, and parameterize nilpotent orbits by partitions. Then we prove the theorem for partitions of length two by an elementary matrix conjugation argument. We finish the proof by induction. The induction argument, however, is not so easy since the statement is not ‘transitive’. For any pair of partitions
$\mathfrak{g}_{n}$
using the trace form, and parameterize nilpotent orbits by partitions. Then we prove the theorem for partitions of length two by an elementary matrix conjugation argument. We finish the proof by induction. The induction argument, however, is not so easy since the statement is not ‘transitive’. For any pair of partitions
![]() $\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}$
(where
$\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}$
(where
![]() ${\leqslant}$
refers to the natural order on partitions which corresponds to the closure order on orbits), we consider two pairs of partitions of two smaller numbers that add up to a number bigger than
${\leqslant}$
refers to the natural order on partitions which corresponds to the closure order on orbits), we consider two pairs of partitions of two smaller numbers that add up to a number bigger than
![]() $n$
. Then we take
$n$
. Then we take
![]() $S^{\prime }$
and
$S^{\prime }$
and
![]() $S^{\prime \prime }$
corresponding to the two pairs of partitions and force them to coincide on the joint block by adding a scalar matrix to one of them. In this way we obtain a diagonal matrix
$S^{\prime \prime }$
corresponding to the two pairs of partitions and force them to coincide on the joint block by adding a scalar matrix to one of them. In this way we obtain a diagonal matrix
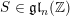 $S\in \mathfrak{gl}_{n}(\mathbb{Z})$
that satisfies the requirements of the theorem.
$S\in \mathfrak{gl}_{n}(\mathbb{Z})$
that satisfies the requirements of the theorem.
For archimedean
![]() $\mathbb{F}$
, Theorem E follows from Theorem B [Reference MatumotoMat87] and Corollary 3.3.7. For non-archimedean
$\mathbb{F}$
, Theorem E follows from Theorem B [Reference MatumotoMat87] and Corollary 3.3.7. For non-archimedean
![]() $\mathbb{F}$
, it was shown in [Reference Moeglin and WaldspurgerMW87] that
$\mathbb{F}$
, it was shown in [Reference Moeglin and WaldspurgerMW87] that
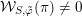 ${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})\neq 0$
for any Whittaker pair
${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})\neq 0$
for any Whittaker pair
![]() $(S,\tilde{\unicode[STIX]{x1D711}})$
such that the orbit of
$(S,\tilde{\unicode[STIX]{x1D711}})$
such that the orbit of
![]() $\tilde{\unicode[STIX]{x1D711}}$
is a maximal orbit in
$\tilde{\unicode[STIX]{x1D711}}$
is a maximal orbit in
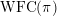 $\operatorname{WFC}(\unicode[STIX]{x1D70B})$
. If
$\operatorname{WFC}(\unicode[STIX]{x1D70B})$
. If
 ${\mathcal{O}}\subset \operatorname{WF}(\unicode[STIX]{x1D70B})$
, then
${\mathcal{O}}\subset \operatorname{WF}(\unicode[STIX]{x1D70B})$
, then
 ${\mathcal{O}}\subset \overline{{\mathcal{O}}^{\prime }}$
for some maximal orbit
${\mathcal{O}}\subset \overline{{\mathcal{O}}^{\prime }}$
for some maximal orbit
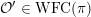 ${\mathcal{O}}^{\prime }\in \operatorname{WFC}(\unicode[STIX]{x1D70B})$
. Pick
${\mathcal{O}}^{\prime }\in \operatorname{WFC}(\unicode[STIX]{x1D70B})$
. Pick
![]() $(S,\tilde{\unicode[STIX]{x1D711}})$
that correspond to
$(S,\tilde{\unicode[STIX]{x1D711}})$
that correspond to
![]() ${\mathcal{O}},{\mathcal{O}}^{\prime }$
by Theorem D. Then, by Theorem A,
${\mathcal{O}},{\mathcal{O}}^{\prime }$
by Theorem D. Then, by Theorem A,
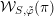 ${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})$
embeds into
${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})$
embeds into
![]() ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
and thus
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
and thus
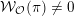 ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
.
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
.
We prove Theorem F by induction on
![]() $k$
. We let
$k$
. We let
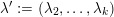 $\unicode[STIX]{x1D706}^{\prime }:=(\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{k})$
, and by the induction hypothesis obtain
$\unicode[STIX]{x1D706}^{\prime }:=(\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{k})$
, and by the induction hypothesis obtain
 $$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}^{\prime }}}\simeq I^{\unicode[STIX]{x1D706}_{2}}(\cdots I^{\unicode[STIX]{x1D706}_{k}}(\mathbb{C})\cdots \,).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}^{\prime }}}\simeq I^{\unicode[STIX]{x1D706}_{2}}(\cdots I^{\unicode[STIX]{x1D706}_{k}}(\mathbb{C})\cdots \,).\end{eqnarray}$$
Thus, in order to prove (4) we have to show that
 $$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}\simeq I^{\unicode[STIX]{x1D706}_{1}}({\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}\simeq I^{\unicode[STIX]{x1D706}_{1}}({\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}).\end{eqnarray}$$
We note that both sides of the formula are isomorphic to inductions of the same character from two nilpotent subgroups that differ only in the last
![]() $\unicode[STIX]{x1D706}_{1}$
columns. Then we prove (6) by a deformation argument similar to the proof of Theorem A. Finally, (5) follows from (4) by a version of Frobenius reciprocity.
$\unicode[STIX]{x1D706}_{1}$
columns. Then we prove (6) by a deformation argument similar to the proof of Theorem A. Finally, (5) follows from (4) by a version of Frobenius reciprocity.
Corollary G follows from (5) using the properties of archimedean prederivatives proven in [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b, Reference Gourevitch and SahiGS13, Reference Gourevitch and SahiGS15].
The proof of Theorem C is analogous to the proofs of Theorems A and D. The only difference is that we cannot apply the Stone–von Neumann theorem since in the global case we consider Whittaker–Fourier coefficients, that are some explicit functionals on an automorphic representation. We replace it by Lemma 6.0.2, that is proven by an explicit integral transform followed by a Fourier transform on a compact abelian group. This lemma is in the spirit of [Reference Ginzburg, Rallis and SoudryGRS11, Propositions 7.2 and 7.3].
If
![]() $\mathbb{F}$
is archimedean, one can consider more general models, and analogs of Theorems A–F will remain valid for them, see Remark 2.5.4.
$\mathbb{F}$
is archimedean, one can consider more general models, and analogs of Theorems A–F will remain valid for them, see Remark 2.5.4.
2 Preliminaries
2.1 Notation
For a semi-simple element
![]() $S$
and a rational number
$S$
and a rational number
![]() $r$
we denote by
$r$
we denote by
![]() $\mathfrak{g}_{r}^{S}$
the
$\mathfrak{g}_{r}^{S}$
the
![]() $r$
-eigenspace of the adjoint action of
$r$
-eigenspace of the adjoint action of
![]() $S$
and by
$S$
and by
![]() $\mathfrak{g}_{{\geqslant}r}^{S}$
the sum
$\mathfrak{g}_{{\geqslant}r}^{S}$
the sum
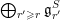 $\bigoplus _{r^{\prime }\geqslant r}\mathfrak{g}_{r^{\prime }}^{S}$
. We will also use the notation
$\bigoplus _{r^{\prime }\geqslant r}\mathfrak{g}_{r^{\prime }}^{S}$
. We will also use the notation
![]() $(\mathfrak{g}^{\ast })_{r}^{S}$
and
$(\mathfrak{g}^{\ast })_{r}^{S}$
and
![]() $(\mathfrak{g}^{\ast })_{{\geqslant}r}^{S}$
for the corresponding grading and filtration of the dual Lie algebra
$(\mathfrak{g}^{\ast })_{{\geqslant}r}^{S}$
for the corresponding grading and filtration of the dual Lie algebra
![]() $\mathfrak{g}^{\ast }$
. For
$\mathfrak{g}^{\ast }$
. For
![]() $X\in \mathfrak{g}$
or
$X\in \mathfrak{g}$
or
![]() $X\in \mathfrak{g}^{\ast }$
we denote by
$X\in \mathfrak{g}^{\ast }$
we denote by
![]() $\mathfrak{g}_{X}$
the centralizer of
$\mathfrak{g}_{X}$
the centralizer of
![]() $X$
in
$X$
in
![]() $\mathfrak{g}$
, and by
$\mathfrak{g}$
, and by
![]() $G_{X}$
the centralizer of
$G_{X}$
the centralizer of
![]() $X$
in
$X$
in
![]() $G$
. We say that an element
$G$
. We say that an element
![]() $h\in \mathfrak{g}$
is rational semi-simple if its adjoint action on
$h\in \mathfrak{g}$
is rational semi-simple if its adjoint action on
![]() $\mathfrak{g}$
is diagonalizable with eigenvalues in
$\mathfrak{g}$
is diagonalizable with eigenvalues in
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
If
![]() $(f,h,e)$
is an
$(f,h,e)$
is an
![]() $\mathfrak{sl}_{2}$
-triple, we will say that
$\mathfrak{sl}_{2}$
-triple, we will say that
![]() $e$
is a nil-positive element for
$e$
is a nil-positive element for
![]() $h$
,
$h$
,
![]() $f$
is a nil-negative element for
$f$
is a nil-negative element for
![]() $h$
and
$h$
and
![]() $h$
is a neutral element for
$h$
is a neutral element for
![]() $e$
. For a representation
$e$
. For a representation
![]() $V$
of
$V$
of
![]() $(f,h,e)$
we denote by
$(f,h,e)$
we denote by
![]() $V^{e}$
the space spanned by the highest-weight vectors and by
$V^{e}$
the space spanned by the highest-weight vectors and by
![]() $V^{f}$
the space spanned by the lowest-weight vectors.
$V^{f}$
the space spanned by the lowest-weight vectors.
From now on we fix a non-trivial unitary additive character
 $$\begin{eqnarray}\unicode[STIX]{x1D712}:\mathbb{F}\rightarrow \text{S}^{1}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}:\mathbb{F}\rightarrow \text{S}^{1}\end{eqnarray}$$
such that if
![]() $\mathbb{F}$
is archimedean we have
$\mathbb{F}$
is archimedean we have
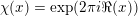 $\unicode[STIX]{x1D712}(x)=\exp (2\unicode[STIX]{x1D70B}i\Re (x))$
and if
$\unicode[STIX]{x1D712}(x)=\exp (2\unicode[STIX]{x1D70B}i\Re (x))$
and if
![]() $\mathbb{F}$
is non-archimedean the kernel of
$\mathbb{F}$
is non-archimedean the kernel of
![]() $\unicode[STIX]{x1D712}$
is the ring of integers.
$\unicode[STIX]{x1D712}$
is the ring of integers.
2.2
 $\mathfrak{sl}_{2}$
-triples
$\mathfrak{sl}_{2}$
-triples
We will need the following lemma which summarizes several well-known facts about
![]() $\mathfrak{sl}_{2}$
-triples.
$\mathfrak{sl}_{2}$
-triples.
Lemma 2.2.1 (See [Reference BourbakiBou75, § 11] or [Reference KostantKos59]).
![]() $\,$
$\,$
-
(i) Any nilpotent element is the nil-positive element of some
 $\mathfrak{sl}_{2}$
-triple in
$\mathfrak{sl}_{2}$
-triple in
 $\mathfrak{g}$
.
$\mathfrak{g}$
. -
(ii) If
 $h$
has a nil-positive element, then
$h$
has a nil-positive element, then
 $e$
is a nil-positive element for
$e$
is a nil-positive element for
 $h$
if and only if
$h$
if and only if
 $e\in \mathfrak{g}_{2}^{h}$
and
$e\in \mathfrak{g}_{2}^{h}$
and
 $\text{ad}(e)$
defines a surjection
$\text{ad}(e)$
defines a surjection
 $\mathfrak{g}_{0}^{h}\,{\twoheadrightarrow}\,\mathfrak{g}_{2}^{h}$
. The set of nil-positive elements for
$\mathfrak{g}_{0}^{h}\,{\twoheadrightarrow}\,\mathfrak{g}_{2}^{h}$
. The set of nil-positive elements for
 $h$
is open in
$h$
is open in
 $\mathfrak{g}_{2}^{h}$
.
$\mathfrak{g}_{2}^{h}$
. -
(iii) If
 $e$
is nilpotent, then
$e$
is nilpotent, then
 $h$
is a neutral element for
$h$
is a neutral element for
 $e$
if and only if
$e$
if and only if
 $e\in \mathfrak{g}_{2}^{h}$
and
$e\in \mathfrak{g}_{2}^{h}$
and
 $h\in \text{Im}(\text{ad}(e))$
. All such
$h\in \text{Im}(\text{ad}(e))$
. All such
 $h$
are conjugate under
$h$
are conjugate under
 $G_{e}$
.
$G_{e}$
. -
(iv) If
 $(f,h,e)$
and
$(f,h,e)$
and
 $(f^{\prime },h,e)$
are
$(f^{\prime },h,e)$
are
 $\mathfrak{sl}_{2}$
-triples, then
$\mathfrak{sl}_{2}$
-triples, then
 $f=f^{\prime }$
.
$f=f^{\prime }$
. -
(v) If
 $(f,h,e)$
is an
$(f,h,e)$
is an
 $\mathfrak{sl}_{2}$
-triple and
$\mathfrak{sl}_{2}$
-triple and
 $Z$
commutes with two of its elements, then it commutes also with the third one.
$Z$
commutes with two of its elements, then it commutes also with the third one.
It is easy to see that the lemma continues to hold true if we replace the nil-positive elements by nil-negative ones (and
![]() $\mathfrak{g}_{2}^{h}$
by
$\mathfrak{g}_{2}^{h}$
by
![]() $\mathfrak{g}_{-2}^{h}$
).
$\mathfrak{g}_{-2}^{h}$
).
Definition 2.2.2. We will say that
![]() $h\in \mathfrak{g}$
is a neutral element for
$h\in \mathfrak{g}$
is a neutral element for
![]() $\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
if
$\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
if
![]() $h$
has a nil-positive element in
$h$
has a nil-positive element in
![]() $\mathfrak{g}$
,
$\mathfrak{g}$
,
 $\unicode[STIX]{x1D711}\in (\mathfrak{g}^{\ast })_{-2}^{h}$
, and the linear map
$\unicode[STIX]{x1D711}\in (\mathfrak{g}^{\ast })_{-2}^{h}$
, and the linear map
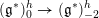 $(\mathfrak{g}^{\ast })_{0}^{h}\rightarrow (\mathfrak{g}^{\ast })_{-2}^{h}$
given by
$(\mathfrak{g}^{\ast })_{0}^{h}\rightarrow (\mathfrak{g}^{\ast })_{-2}^{h}$
given by
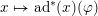 $x\mapsto \text{ad}^{\ast }(x)(\unicode[STIX]{x1D711})$
is an epimorphism. Note that if we identify
$x\mapsto \text{ad}^{\ast }(x)(\unicode[STIX]{x1D711})$
is an epimorphism. Note that if we identify
![]() $\mathfrak{g}$
with
$\mathfrak{g}$
with
![]() $\mathfrak{g}^{\ast }$
(in a
$\mathfrak{g}^{\ast }$
(in a
![]() $G$
-equivariant way) this property becomes equivalent to
$G$
-equivariant way) this property becomes equivalent to
![]() $\unicode[STIX]{x1D711}$
being a nil-negative element for
$\unicode[STIX]{x1D711}$
being a nil-negative element for
![]() $h$
, or
$h$
, or
![]() $-h$
being a neutral element for
$-h$
being a neutral element for
![]() $\unicode[STIX]{x1D711}$
. We also say that
$\unicode[STIX]{x1D711}$
. We also say that
![]() $0\in \mathfrak{g}$
is a neutral element for
$0\in \mathfrak{g}$
is a neutral element for
![]() $0\in \mathfrak{g}^{\ast }$
.
$0\in \mathfrak{g}^{\ast }$
.
2.3 Schwartz induction
Definition 2.3.1. If
![]() $G$
is an
$G$
is an
![]() $l$
-group, we denote by
$l$
-group, we denote by
 $\text{Rep}^{\infty }(G)$
the category of smooth representations of
$\text{Rep}^{\infty }(G)$
the category of smooth representations of
![]() $G$
. If
$G$
. If
![]() $H\subset G$
is a closed subgroup and
$H\subset G$
is a closed subgroup and
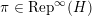 $\unicode[STIX]{x1D70B}\in \text{Rep}^{\infty }(H)$
is a smooth representation of
$\unicode[STIX]{x1D70B}\in \text{Rep}^{\infty }(H)$
is a smooth representation of
![]() $G$
, we denote by
$G$
, we denote by
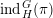 $\text{ind}_{H}^{G}(\unicode[STIX]{x1D70B})$
the smooth compactly supported induction as in [Reference Bernstein and ZelevinskyBZ76, § 2.22].
$\text{ind}_{H}^{G}(\unicode[STIX]{x1D70B})$
the smooth compactly supported induction as in [Reference Bernstein and ZelevinskyBZ76, § 2.22].
If
![]() $G$
is an affine real algebraic group, we denote by
$G$
is an affine real algebraic group, we denote by
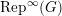 $\text{Rep}^{\infty }(G)$
the category of smooth nuclear Fréchet representations of
$\text{Rep}^{\infty }(G)$
the category of smooth nuclear Fréchet representations of
![]() $G$
of moderate growth. This is essentially the same definition as in [Reference du ClouxdCl91, § 1.4] with the additional assumption that the representation spaces are nuclear (see e.g. [Reference TrevesTre67, § 50]). If
$G$
of moderate growth. This is essentially the same definition as in [Reference du ClouxdCl91, § 1.4] with the additional assumption that the representation spaces are nuclear (see e.g. [Reference TrevesTre67, § 50]). If
![]() $H\subset G$
is a Zariski closed subgroup, and
$H\subset G$
is a Zariski closed subgroup, and
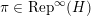 $\unicode[STIX]{x1D70B}\in \text{Rep}^{\infty }(H)$
we denote by
$\unicode[STIX]{x1D70B}\in \text{Rep}^{\infty }(H)$
we denote by
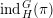 $\text{ind}_{H}^{G}(\unicode[STIX]{x1D70B})$
the Schwartz induction as in [Reference du ClouxdCl91, § 2]. More precisely, in [Reference du ClouxdCl91] du Cloux defines a map from the space
$\text{ind}_{H}^{G}(\unicode[STIX]{x1D70B})$
the Schwartz induction as in [Reference du ClouxdCl91, § 2]. More precisely, in [Reference du ClouxdCl91] du Cloux defines a map from the space
![]() ${\mathcal{S}}(G,\unicode[STIX]{x1D70B})$
of Schwartz functions from
${\mathcal{S}}(G,\unicode[STIX]{x1D70B})$
of Schwartz functions from
![]() $G$
to the underlying space of
$G$
to the underlying space of
![]() $\unicode[STIX]{x1D70B}$
to the space
$\unicode[STIX]{x1D70B}$
to the space
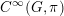 $C^{\infty }(G,\unicode[STIX]{x1D70B})$
of all smooth
$C^{\infty }(G,\unicode[STIX]{x1D70B})$
of all smooth
![]() $\unicode[STIX]{x1D70B}$
-valued functions on
$\unicode[STIX]{x1D70B}$
-valued functions on
![]() $G$
by
$G$
by
![]() $f\mapsto \overline{f}$
where
$f\mapsto \overline{f}$
where
 $$\begin{eqnarray}\overline{f}(x)=\int _{h\in H}\unicode[STIX]{x1D70B}(h)f(xh)\,dh,\end{eqnarray}$$
$$\begin{eqnarray}\overline{f}(x)=\int _{h\in H}\unicode[STIX]{x1D70B}(h)f(xh)\,dh,\end{eqnarray}$$
and
![]() $dh$
denotes a fixed left-invariant measure on
$dh$
denotes a fixed left-invariant measure on
![]() $H$
. The Schwartz induction
$H$
. The Schwartz induction
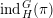 $\text{ind}_{H}^{G}(\unicode[STIX]{x1D70B})$
is defined to be the image of this map.
$\text{ind}_{H}^{G}(\unicode[STIX]{x1D70B})$
is defined to be the image of this map.
From now until the end of the subsection let
![]() $G$
be either an
$G$
be either an
![]() $l$
-group or an affine real algebraic group, and
$l$
-group or an affine real algebraic group, and
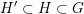 $H^{\prime }\subset H\subset G$
be (Zariski) closed subgroups.
$H^{\prime }\subset H\subset G$
be (Zariski) closed subgroups.
Lemma 2.3.2 ([Reference Bernstein and ZelevinskyBZ76, Proposition 2.25(b)] and [Reference du ClouxdCl91, Lemma 2.1.6]).
For any
 $\unicode[STIX]{x1D70B}\in \text{Rep}^{\infty }(H^{\prime })$
we have
$\unicode[STIX]{x1D70B}\in \text{Rep}^{\infty }(H^{\prime })$
we have
 $$\begin{eqnarray}\text{ind}_{H^{\prime }}^{G}(\unicode[STIX]{x1D70B})\simeq \text{ind}_{H}^{G}\,\text{ind}_{H^{\prime }}^{H}(\unicode[STIX]{x1D70B}).\end{eqnarray}$$
$$\begin{eqnarray}\text{ind}_{H^{\prime }}^{G}(\unicode[STIX]{x1D70B})\simeq \text{ind}_{H}^{G}\,\text{ind}_{H^{\prime }}^{H}(\unicode[STIX]{x1D70B}).\end{eqnarray}$$
Corollary 2.3.3. For any
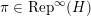 $\unicode[STIX]{x1D70B}\in \text{Rep}^{\infty }(H)$
we have a natural epimorphism
$\unicode[STIX]{x1D70B}\in \text{Rep}^{\infty }(H)$
we have a natural epimorphism
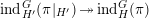 $\text{ind}_{H^{\prime }}^{G}(\unicode[STIX]{x1D70B}|_{H^{\prime }})\,{\twoheadrightarrow}\,\text{ind}_{H}^{G}(\unicode[STIX]{x1D70B})$
.
$\text{ind}_{H^{\prime }}^{G}(\unicode[STIX]{x1D70B}|_{H^{\prime }})\,{\twoheadrightarrow}\,\text{ind}_{H}^{G}(\unicode[STIX]{x1D70B})$
.
Lemma 2.3.4. Let
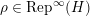 $\unicode[STIX]{x1D70C}\in \text{Rep}^{\infty }(H)$
,
$\unicode[STIX]{x1D70C}\in \text{Rep}^{\infty }(H)$
,
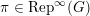 $\unicode[STIX]{x1D70B}\in \text{Rep}^{\infty }(G)$
and let
$\unicode[STIX]{x1D70B}\in \text{Rep}^{\infty }(G)$
and let
![]() $\unicode[STIX]{x1D70B}^{\ast }$
denote the dual representation, (endowed with the strong dual topology in the archimedean case). Then
$\unicode[STIX]{x1D70B}^{\ast }$
denote the dual representation, (endowed with the strong dual topology in the archimedean case). Then
 $$\begin{eqnarray}\text{Hom}_{G}(\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C}),\unicode[STIX]{x1D70B}^{\ast })\cong \text{Hom}_{H}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E5}_{H}^{-1}\unicode[STIX]{x1D6E5}_{G}),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{G}(\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C}),\unicode[STIX]{x1D70B}^{\ast })\cong \text{Hom}_{H}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E5}_{H}^{-1}\unicode[STIX]{x1D6E5}_{G}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E5}_{H}$
and
$\unicode[STIX]{x1D6E5}_{H}$
and
![]() $\unicode[STIX]{x1D6E5}_{G}$
denote the modular functions of
$\unicode[STIX]{x1D6E5}_{G}$
denote the modular functions of
![]() $H$
and
$H$
and
![]() $G$
.
$G$
.
The non-archimedean case of this lemma follows from [Reference Bernstein and ZelevinskyBZ76, Proposition 2.29]. We prove the archimedean case in Appendix A. We will only use this lemma in the case when
![]() $G$
is reductive,
$G$
is reductive,
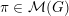 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
,
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
,
![]() $H$
is nilpotent and
$H$
is nilpotent and
![]() $\unicode[STIX]{x1D70C}$
is one-dimensional.
$\unicode[STIX]{x1D70C}$
is one-dimensional.
2.4 Oscillator representations of the Heisenberg group
Definition 2.4.1. Let
![]() $W_{n}$
denote the
$W_{n}$
denote the
![]() $2n$
-dimensional
$2n$
-dimensional
![]() $\mathbb{F}$
-vector space
$\mathbb{F}$
-vector space
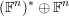 $(\mathbb{F}^{n})^{\ast }\oplus \mathbb{F}^{n}$
and let
$(\mathbb{F}^{n})^{\ast }\oplus \mathbb{F}^{n}$
and let
![]() $\unicode[STIX]{x1D714}$
be the standard symplectic form on
$\unicode[STIX]{x1D714}$
be the standard symplectic form on
![]() $W_{n}$
. The Heisenberg group
$W_{n}$
. The Heisenberg group
![]() $H_{n}$
is the algebraic group with underlying algebraic variety
$H_{n}$
is the algebraic group with underlying algebraic variety
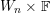 $W_{n}\times \mathbb{F}$
with the group law given by
$W_{n}\times \mathbb{F}$
with the group law given by
 $$\begin{eqnarray}(w_{1},z_{1})(w_{2},z_{2})=(w_{1}+w_{2},z_{1}+z_{2}+1/2\unicode[STIX]{x1D714}(w_{1},w_{2})).\end{eqnarray}$$
$$\begin{eqnarray}(w_{1},z_{1})(w_{2},z_{2})=(w_{1}+w_{2},z_{1}+z_{2}+1/2\unicode[STIX]{x1D714}(w_{1},w_{2})).\end{eqnarray}$$
Note that
![]() $H_{0}=\mathbb{F}$
.
$H_{0}=\mathbb{F}$
.
Definition 2.4.2. Let
![]() $\unicode[STIX]{x1D712}$
be the additive character of
$\unicode[STIX]{x1D712}$
be the additive character of
![]() $\mathbb{F}$
, as in (7). Extend
$\mathbb{F}$
, as in (7). Extend
![]() $\unicode[STIX]{x1D712}$
trivially to a character of the commutative subgroup
$\unicode[STIX]{x1D712}$
trivially to a character of the commutative subgroup
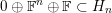 $0\oplus \mathbb{F}^{n}\oplus \mathbb{F}\subset H_{n}$
. The oscillator representation
$0\oplus \mathbb{F}^{n}\oplus \mathbb{F}\subset H_{n}$
. The oscillator representation
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D712}}$
is the unitary induction of
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D712}}$
is the unitary induction of
![]() $\unicode[STIX]{x1D712}$
from
$\unicode[STIX]{x1D712}$
from
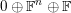 $0\oplus \mathbb{F}^{n}\oplus \mathbb{F}$
to
$0\oplus \mathbb{F}^{n}\oplus \mathbb{F}$
to
![]() $H_{n}$
. Define the smooth oscillator representation
$H_{n}$
. Define the smooth oscillator representation
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}$
to be the space of smooth vectors in
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}$
to be the space of smooth vectors in
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D712}}$
.
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D712}}$
.
Lemma 2.4.3. We have
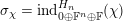 $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}=\text{ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712})$
.
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}=\text{ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712})$
.
Proof. In the archimedean case we apply the characterization of smooth vectors in a unitary induction given in [Reference PoulsenPou72, Theorem 5.1]. By this characterization
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}$
can be identified with the space
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}$
can be identified with the space
 $$\begin{eqnarray}\{f\in C^{\infty }((\mathbb{F}^{n})^{\ast })\,|\,x^{i}f^{(j)}\in L^{2}((\mathbb{F}^{n})^{\ast })\,\forall i,j\}.\end{eqnarray}$$
$$\begin{eqnarray}\{f\in C^{\infty }((\mathbb{F}^{n})^{\ast })\,|\,x^{i}f^{(j)}\in L^{2}((\mathbb{F}^{n})^{\ast })\,\forall i,j\}.\end{eqnarray}$$
This space coincides with the Schwartz space
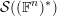 ${\mathcal{S}}((\mathbb{F}^{n})^{\ast })$
, which in turn can be identified with
${\mathcal{S}}((\mathbb{F}^{n})^{\ast })$
, which in turn can be identified with
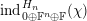 $\text{ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712})$
.
$\text{ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712})$
.
In the non-archimedean case let us prove a stronger statement:
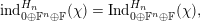 $\text{ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712})=\text{Ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712}),$
where
$\text{ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712})=\text{Ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712}),$
where
![]() $\text{Ind}$
denotes the full smooth induction. Indeed let
$\text{Ind}$
denotes the full smooth induction. Indeed let
 $f\in \text{Ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712}),$
and let
$f\in \text{Ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712}),$
and let
![]() $f^{\prime }$
be the restriction of
$f^{\prime }$
be the restriction of
![]() $f$
to
$f$
to
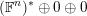 $(\mathbb{F}^{n})^{\ast }\oplus 0\oplus 0$
. Since
$(\mathbb{F}^{n})^{\ast }\oplus 0\oplus 0$
. Since
![]() $f$
is smooth, i.e. fixed by an open compact subgroup
$f$
is smooth, i.e. fixed by an open compact subgroup
![]() $K$
of
$K$
of
![]() $H_{n}$
, for any
$H_{n}$
, for any
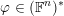 $\unicode[STIX]{x1D711}\in (\mathbb{F}^{n})^{\ast }$
and
$\unicode[STIX]{x1D711}\in (\mathbb{F}^{n})^{\ast }$
and
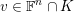 $v\in \mathbb{F}^{n}\cap K$
we have
$v\in \mathbb{F}^{n}\cap K$
we have
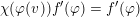 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(v))f^{\prime }(\unicode[STIX]{x1D711})=f^{\prime }(\unicode[STIX]{x1D711})$
. This implies that
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(v))f^{\prime }(\unicode[STIX]{x1D711})=f^{\prime }(\unicode[STIX]{x1D711})$
. This implies that
![]() $f^{\prime }$
has compact support, and thus
$f^{\prime }$
has compact support, and thus
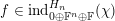 $f\in \text{ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712})$
.◻
$f\in \text{ind}_{0\oplus \mathbb{F}^{n}\oplus \mathbb{F}}^{H_{n}}(\unicode[STIX]{x1D712})$
.◻
Theorem 2.4.4 (Stone–von Neumann).
The oscillator representation
![]() $\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D712}}$
is the only irreducible unitary representation of
$\unicode[STIX]{x1D71B}_{\unicode[STIX]{x1D712}}$
is the only irreducible unitary representation of
![]() $H_{n}$
with central character
$H_{n}$
with central character
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
Corollary 2.4.5. Let
![]() $L\subset W$
be a Lagrangian subspace. Extend
$L\subset W$
be a Lagrangian subspace. Extend
![]() $\unicode[STIX]{x1D712}$
trivially to the abelian subgroup
$\unicode[STIX]{x1D712}$
trivially to the abelian subgroup
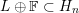 $L\oplus \mathbb{F}\subset H_{n}$
. Then
$L\oplus \mathbb{F}\subset H_{n}$
. Then
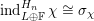 $\text{ind}_{L\oplus \mathbb{F}}^{H_{n}}\,\unicode[STIX]{x1D712}\cong \unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}$
.
$\text{ind}_{L\oplus \mathbb{F}}^{H_{n}}\,\unicode[STIX]{x1D712}\cong \unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}$
.
Lemma 2.4.6. Let
![]() $\mathbb{F}$
be non-archimedean. Let
$\mathbb{F}$
be non-archimedean. Let
![]() $\unicode[STIX]{x1D70F}$
be a smooth representation of
$\unicode[STIX]{x1D70F}$
be a smooth representation of
![]() $H_{n}$
on which the center acts by the character
$H_{n}$
on which the center acts by the character
![]() $\unicode[STIX]{x1D712}$
, and let
$\unicode[STIX]{x1D712}$
, and let
![]() $\widetilde{\unicode[STIX]{x1D70F}}$
denote the smooth contragredient. Then
$\widetilde{\unicode[STIX]{x1D70F}}$
denote the smooth contragredient. Then
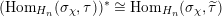 $(\text{Hom}_{H_{n}}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D70F}))^{\ast }\cong \text{Hom}_{H_{n}}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}},\widetilde{\unicode[STIX]{x1D70F}})$
.
$(\text{Hom}_{H_{n}}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D70F}))^{\ast }\cong \text{Hom}_{H_{n}}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}},\widetilde{\unicode[STIX]{x1D70F}})$
.
Proof. Let
![]() $L\subset W$
be a maximal lattice such that
$L\subset W$
be a maximal lattice such that
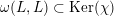 $\unicode[STIX]{x1D714}(L,L)\subset \text{Ker}(\unicode[STIX]{x1D712})$
. Then by Theorem 2.4.4
$\unicode[STIX]{x1D714}(L,L)\subset \text{Ker}(\unicode[STIX]{x1D712})$
. Then by Theorem 2.4.4
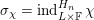 $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}=\text{ind}_{L\times \mathbb{F}}^{H_{n}}\,\unicode[STIX]{x1D712}$
. By [Reference Bernstein and ZelevinskyBZ76, 2.29]
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}=\text{ind}_{L\times \mathbb{F}}^{H_{n}}\,\unicode[STIX]{x1D712}$
. By [Reference Bernstein and ZelevinskyBZ76, 2.29]
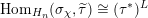 $\text{Hom}_{H_{n}}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}},\widetilde{\unicode[STIX]{x1D70F}})\cong (\unicode[STIX]{x1D70F}^{\ast })^{L}$
. Since
$\text{Hom}_{H_{n}}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}},\widetilde{\unicode[STIX]{x1D70F}})\cong (\unicode[STIX]{x1D70F}^{\ast })^{L}$
. Since
![]() $L$
is an open compact subgroup we get
$L$
is an open compact subgroup we get
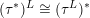 $(\unicode[STIX]{x1D70F}^{\ast })^{L}\cong (\unicode[STIX]{x1D70F}^{L})^{\ast }$
and
$(\unicode[STIX]{x1D70F}^{\ast })^{L}\cong (\unicode[STIX]{x1D70F}^{L})^{\ast }$
and
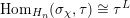 $\text{Hom}_{H_{n}}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D70F})\cong \unicode[STIX]{x1D70F}^{L}$
.◻
$\text{Hom}_{H_{n}}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D70F})\cong \unicode[STIX]{x1D70F}^{L}$
.◻
2.5 Degenerate Whittaker models
Definition 2.5.1. (i) A Whittaker pair is an ordered pair
![]() $(S,\unicode[STIX]{x1D711})$
such that
$(S,\unicode[STIX]{x1D711})$
such that
![]() $S\in \mathfrak{g}$
is rational semi-simple, and
$S\in \mathfrak{g}$
is rational semi-simple, and
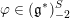 $\unicode[STIX]{x1D711}\in (\mathfrak{g}^{\ast })_{-2}^{S}$
. Given such a Whittaker pair, we define the space of degenerate Whittaker models
$\unicode[STIX]{x1D711}\in (\mathfrak{g}^{\ast })_{-2}^{S}$
. Given such a Whittaker pair, we define the space of degenerate Whittaker models
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
in the following way: let
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
in the following way: let
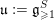 $\mathfrak{u}:=\mathfrak{g}_{{\geqslant}1}^{S}$
. Define an anti-symmetric form
$\mathfrak{u}:=\mathfrak{g}_{{\geqslant}1}^{S}$
. Define an anti-symmetric form
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}$
on
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}$
on
![]() $\mathfrak{g}$
by
$\mathfrak{g}$
by
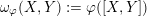 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}(X,Y):=\unicode[STIX]{x1D711}([X,Y])$
. Let
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}(X,Y):=\unicode[STIX]{x1D711}([X,Y])$
. Let
![]() $\mathfrak{n}$
be the radical of
$\mathfrak{n}$
be the radical of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}|_{\mathfrak{u}}$
. Note that
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}|_{\mathfrak{u}}$
. Note that
![]() $\mathfrak{u},\mathfrak{n}$
are nilpotent subalgebras of
$\mathfrak{u},\mathfrak{n}$
are nilpotent subalgebras of
![]() $\mathfrak{g}$
, and
$\mathfrak{g}$
, and
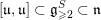 $[\mathfrak{u},\mathfrak{u}]\subset \mathfrak{g}_{{\geqslant}2}^{S}\subset \mathfrak{n}$
. Let
$[\mathfrak{u},\mathfrak{u}]\subset \mathfrak{g}_{{\geqslant}2}^{S}\subset \mathfrak{n}$
. Let
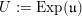 $U:=\text{Exp}(\mathfrak{u})$
and
$U:=\text{Exp}(\mathfrak{u})$
and
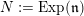 $N:=\text{Exp}(\mathfrak{n})$
be the corresponding nilpotent subgroups of
$N:=\text{Exp}(\mathfrak{n})$
be the corresponding nilpotent subgroups of
![]() $G$
. Let
$G$
. Let
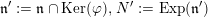 $\mathfrak{n}^{\prime }:=\mathfrak{n}\cap \text{Ker}(\unicode[STIX]{x1D711}),\,N^{\prime }:=\text{Exp}(\mathfrak{n}^{\prime })$
. If
$\mathfrak{n}^{\prime }:=\mathfrak{n}\cap \text{Ker}(\unicode[STIX]{x1D711}),\,N^{\prime }:=\text{Exp}(\mathfrak{n}^{\prime })$
. If
![]() $\unicode[STIX]{x1D711}=0$
we define
$\unicode[STIX]{x1D711}=0$
we define
 $$\begin{eqnarray}{\mathcal{W}}_{S,0}:=\text{ind}_{U}^{G}(\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{S,0}:=\text{ind}_{U}^{G}(\mathbb{C}).\end{eqnarray}$$
Assume now that
![]() $\unicode[STIX]{x1D711}$
is non-zero. Then
$\unicode[STIX]{x1D711}$
is non-zero. Then
![]() $U/N^{\prime }$
has a natural structure of a Heisenberg group, and its center is
$U/N^{\prime }$
has a natural structure of a Heisenberg group, and its center is
![]() $N/N^{\prime }$
. Let
$N/N^{\prime }$
. Let
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
denote the unitary character of
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
denote the unitary character of
![]() $N/N^{\prime }$
given by
$N/N^{\prime }$
given by
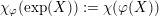 $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}(\exp (X)):=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(X))$
. Let
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}(\exp (X)):=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(X))$
. Let
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
denote the oscillator representation of
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
denote the oscillator representation of
![]() $U/N^{\prime }$
with central character
$U/N^{\prime }$
with central character
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
, and
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
, and
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}^{\prime }$
denote its trivial lifting to
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}^{\prime }$
denote its trivial lifting to
![]() $U$
. Define
$U$
. Define
 $$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}:=\text{ind}_{U}^{G}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}:=\text{ind}_{U}^{G}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}^{\prime }).\end{eqnarray}$$
(ii) For a nilpotent element
![]() $\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
, define the generalized Whittaker model
$\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
, define the generalized Whittaker model
![]() ${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
corresponding to
${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
corresponding to
![]() $\unicode[STIX]{x1D711}$
to be
$\unicode[STIX]{x1D711}$
to be
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
, where
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
, where
![]() $S$
is a neutral element for
$S$
is a neutral element for
![]() $\unicode[STIX]{x1D711}$
if
$\unicode[STIX]{x1D711}$
if
![]() $\unicode[STIX]{x1D711}\neq 0$
and
$\unicode[STIX]{x1D711}\neq 0$
and
![]() $S=0$
if
$S=0$
if
![]() $\unicode[STIX]{x1D711}=0$
. We will also call
$\unicode[STIX]{x1D711}=0$
. We will also call
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
neutral degenerate Whittaker model. By Lemma 2.2.1
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
neutral degenerate Whittaker model. By Lemma 2.2.1
![]() ${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
depends only on the coadjoint orbit of
${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
depends only on the coadjoint orbit of
![]() $\unicode[STIX]{x1D711}$
, and does not depend on the choice of
$\unicode[STIX]{x1D711}$
, and does not depend on the choice of
![]() $S$
. Thus, we will also use the notation
$S$
. Thus, we will also use the notation
![]() ${\mathcal{W}}_{{\mathcal{O}}}$
for a nilpotent coadjoint orbit
${\mathcal{W}}_{{\mathcal{O}}}$
for a nilpotent coadjoint orbit
![]() ${\mathcal{O}}\subset \mathfrak{g}^{\ast }$
. In § 5 we reformulate this definition without choosing
${\mathcal{O}}\subset \mathfrak{g}^{\ast }$
. In § 5 we reformulate this definition without choosing
![]() $S$
, but using the Killing form.
$S$
, but using the Killing form.
(iii) For
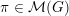 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
define the degenerate and generalized Whittaker spaces of
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
define the degenerate and generalized Whittaker spaces of
![]() $\unicode[STIX]{x1D70B}$
by
$\unicode[STIX]{x1D70B}$
by
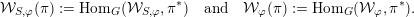 $$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}):=\text{Hom}_{G}({\mathcal{W}}_{S,\unicode[STIX]{x1D711}},\unicode[STIX]{x1D70B}^{\ast })\quad \text{and}\quad {\mathcal{W}}_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}):=\text{Hom}_{G}({\mathcal{W}}_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D70B}^{\ast }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}):=\text{Hom}_{G}({\mathcal{W}}_{S,\unicode[STIX]{x1D711}},\unicode[STIX]{x1D70B}^{\ast })\quad \text{and}\quad {\mathcal{W}}_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}):=\text{Hom}_{G}({\mathcal{W}}_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D70B}^{\ast }).\end{eqnarray}$$
Note that
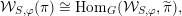 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\cong \text{Hom}_{G}({\mathcal{W}}_{S,\unicode[STIX]{x1D711}},\widetilde{\unicode[STIX]{x1D70B}}),$
where
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\cong \text{Hom}_{G}({\mathcal{W}}_{S,\unicode[STIX]{x1D711}},\widetilde{\unicode[STIX]{x1D70B}}),$
where
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
denotes the contragredient representation. In the non-archimedean case this is obvious and in the archimedean case this follows from the Dixmier–Malliavin theorem [Reference Dixmier and MalliavinDM78].
$\widetilde{\unicode[STIX]{x1D70B}}$
denotes the contragredient representation. In the non-archimedean case this is obvious and in the archimedean case this follows from the Dixmier–Malliavin theorem [Reference Dixmier and MalliavinDM78].
Lemma 2.5.2. Let
![]() $\mathfrak{l}\subset \mathfrak{u}$
be a maximal isotropic subalgebra and
$\mathfrak{l}\subset \mathfrak{u}$
be a maximal isotropic subalgebra and
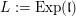 $L:=\text{Exp}(\mathfrak{l})$
. Let
$L:=\text{Exp}(\mathfrak{l})$
. Let
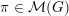 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
. Then
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
. Then
 $$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\cong \text{Hom}_{L}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{-1}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\cong \text{Hom}_{L}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{-1}).\end{eqnarray}$$
Proof. By Corollary 2.4.5 and Lemma 2.3.2 we have
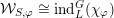 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}\cong \text{ind}_{L}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})$
. Using Lemma 2.3.4 we obtain
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}\cong \text{ind}_{L}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})$
. Using Lemma 2.3.4 we obtain
 $$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\cong \text{Hom}_{G}(\text{ind}_{L}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}),\unicode[STIX]{x1D70B}^{\ast })\cong \text{Hom}_{L}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D70B}^{\ast })\cong \text{Hom}_{L}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{-1}).\square\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\cong \text{Hom}_{G}(\text{ind}_{L}^{G}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}),\unicode[STIX]{x1D70B}^{\ast })\cong \text{Hom}_{L}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D70B}^{\ast })\cong \text{Hom}_{L}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{-1}).\square\end{eqnarray}$$
In the case when
![]() $\mathbb{F}$
is non-archimedean and
$\mathbb{F}$
is non-archimedean and
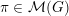 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
, slightly different degenerate Whittaker models are considered in [Reference Moeglin and WaldspurgerMW87]. Namely, let
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
, slightly different degenerate Whittaker models are considered in [Reference Moeglin and WaldspurgerMW87]. Namely, let
![]() $U^{\prime \prime }$
denote the subgroup of
$U^{\prime \prime }$
denote the subgroup of
![]() $U$
generated by
$U$
generated by
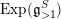 $\text{Exp}(\mathfrak{g}_{{>}1}^{S})$
and the kernel of
$\text{Exp}(\mathfrak{g}_{{>}1}^{S})$
and the kernel of
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. Let
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. Let
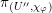 $\unicode[STIX]{x1D70B}_{(U^{\prime \prime },\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})}$
denote the biggest quotient of
$\unicode[STIX]{x1D70B}_{(U^{\prime \prime },\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})}$
denote the biggest quotient of
![]() $\unicode[STIX]{x1D70B}$
on which
$\unicode[STIX]{x1D70B}$
on which
![]() $U^{\prime \prime }$
acts by the character
$U^{\prime \prime }$
acts by the character
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. Then [Reference Moeglin and WaldspurgerMW87] considers
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. Then [Reference Moeglin and WaldspurgerMW87] considers
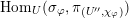 $\text{Hom}_{U}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D70B}_{(U^{\prime \prime },\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})})$
. By Lemma 2.4.6 and Frobenius reciprocity we have
$\text{Hom}_{U}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D70B}_{(U^{\prime \prime },\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})})$
. By Lemma 2.4.6 and Frobenius reciprocity we have
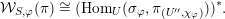 $$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\cong (\text{Hom}_{U}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D70B}_{(U^{\prime \prime },\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})}))^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\cong (\text{Hom}_{U}(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D70B}_{(U^{\prime \prime },\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})}))^{\ast }.\end{eqnarray}$$
Remark 2.5.3. For non-archimedean
![]() $\mathbb{F}$
we can define
$\mathbb{F}$
we can define
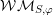 ${\mathcal{W}}{\mathcal{M}}_{S,\unicode[STIX]{x1D711}}$
to be the full induction
${\mathcal{W}}{\mathcal{M}}_{S,\unicode[STIX]{x1D711}}$
to be the full induction
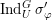 $\text{Ind}_{U}^{G}\,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}^{\prime }$
. Since for
$\text{Ind}_{U}^{G}\,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}^{\prime }$
. Since for
![]() $L$
as in Lemma 2.5.2 we have
$L$
as in Lemma 2.5.2 we have
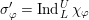 $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}^{\prime }=\text{Ind}_{L}^{U}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
, our proof of Theorem A will show that under the under the conditions of this theorem we have a
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}^{\prime }=\text{Ind}_{L}^{U}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
, our proof of Theorem A will show that under the under the conditions of this theorem we have a
![]() $G$
-equivariant embedding
$G$
-equivariant embedding
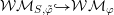 ${\mathcal{W}}{\mathcal{M}}_{S,\tilde{\unicode[STIX]{x1D711}}}{\hookrightarrow}{\mathcal{W}}{\mathcal{M}}_{\unicode[STIX]{x1D711}}$
. For
${\mathcal{W}}{\mathcal{M}}_{S,\tilde{\unicode[STIX]{x1D711}}}{\hookrightarrow}{\mathcal{W}}{\mathcal{M}}_{\unicode[STIX]{x1D711}}$
. For
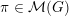 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
one can define
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
one can define
 ${\mathcal{W}}{\mathcal{M}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}):=\text{Hom}_{G}(\unicode[STIX]{x1D70B},{\mathcal{W}}{\mathcal{M}}_{S,\unicode[STIX]{x1D711}})$
. By the Frobenius reciprocity [Reference Bernstein and ZelevinskyBZ76, Theorem 2.28] we have
${\mathcal{W}}{\mathcal{M}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}):=\text{Hom}_{G}(\unicode[STIX]{x1D70B},{\mathcal{W}}{\mathcal{M}}_{S,\unicode[STIX]{x1D711}})$
. By the Frobenius reciprocity [Reference Bernstein and ZelevinskyBZ76, Theorem 2.28] we have
 ${\mathcal{W}}{\mathcal{M}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})=\text{Hom}_{L}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})$
which by Lemma 2.5.2 is isomorphic to
${\mathcal{W}}{\mathcal{M}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})=\text{Hom}_{L}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})$
which by Lemma 2.5.2 is isomorphic to
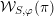 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
. Thus, all of the results of the paper can be reformulated in terms of the full induction.
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
. Thus, all of the results of the paper can be reformulated in terms of the full induction.
In order to have an analogous formulation in the archimedean case one needs a notion of full induction of smooth Fréchet representations of moderate growth, that will satisfy transitivity of induction, Frobenius reciprocity (as in [Reference Bernstein and ZelevinskyBZ76, Theorem 2.28]) and
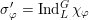 $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}^{\prime }=\text{Ind}_{L}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. A certain full induction
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}^{\prime }=\text{Ind}_{L}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. A certain full induction
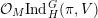 ${\mathcal{O}}_{M}\text{Ind}_{H}^{G}(\unicode[STIX]{x1D70B},V)$
is defined in [Reference du ClouxdCl91, Definition 2.1.3]. It consists of functions of moderate growth from
${\mathcal{O}}_{M}\text{Ind}_{H}^{G}(\unicode[STIX]{x1D70B},V)$
is defined in [Reference du ClouxdCl91, Definition 2.1.3]. It consists of functions of moderate growth from
![]() $G$
to
$G$
to
![]() $V$
which are equivariant under
$V$
which are equivariant under
![]() $H$
. It satisfies the first two of our requirements but not the third. Probably in the suitable notion of full induction the definition of function of moderate growth should take into account the action of
$H$
. It satisfies the first two of our requirements but not the third. Probably in the suitable notion of full induction the definition of function of moderate growth should take into account the action of
![]() $H$
on
$H$
on
![]() $V$
.
$V$
.
Remark 2.5.4. If
![]() $\mathbb{F}$
is archimedean, one can define
$\mathbb{F}$
is archimedean, one can define
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
for any semi-simple
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
for any semi-simple
![]() $S$
with real eigenvalues in the same way, and the proof of Theorem A will be valid for this case without changes.
$S$
with real eigenvalues in the same way, and the proof of Theorem A will be valid for this case without changes.
3 Proof of Theorem A
We will prove in § 3.2 the following generalization of Theorem A.
Theorem 3.0.1. Let
![]() $(S,\unicode[STIX]{x1D711})$
and
$(S,\unicode[STIX]{x1D711})$
and
![]() $(\widetilde{S},\tilde{\unicode[STIX]{x1D711}})$
be two Whittaker pairs in
$(\widetilde{S},\tilde{\unicode[STIX]{x1D711}})$
be two Whittaker pairs in
![]() $\mathfrak{g}$
such that
$\mathfrak{g}$
such that
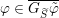 $\unicode[STIX]{x1D711}\in \overline{G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}}$
. Suppose that
$\unicode[STIX]{x1D711}\in \overline{G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}}$
. Suppose that
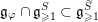 $\mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{g}_{{\geqslant}1}^{S}\subset \mathfrak{g}_{{\geqslant}1}^{\widetilde{S}}$
and that there exists a neutral element
$\mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{g}_{{\geqslant}1}^{S}\subset \mathfrak{g}_{{\geqslant}1}^{\widetilde{S}}$
and that there exists a neutral element
![]() $h$
for
$h$
for
![]() $\unicode[STIX]{x1D711}$
such that
$\unicode[STIX]{x1D711}$
such that
![]() $h$
commutes with
$h$
commutes with
![]() $S$
and
$S$
and
![]() $\widetilde{S}$
, and
$\widetilde{S}$
, and
![]() $S-h$
commutes with
$S-h$
commutes with
![]() $\tilde{\unicode[STIX]{x1D711}}$
. Then there is a
$\tilde{\unicode[STIX]{x1D711}}$
. Then there is a
![]() $G$
-equivariant epimorphism of
$G$
-equivariant epimorphism of
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
onto
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
onto
![]() ${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}$
.
${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}$
.
In order to deduce Theorem A we will need the following lemma.
Lemma 3.0.2 (See § 3.1).
Let
![]() ${\mathcal{P}}$
denote the set of conjugacy classes of Whittaker pairs in
${\mathcal{P}}$
denote the set of conjugacy classes of Whittaker pairs in
![]() $\mathfrak{g}$
and let
$\mathfrak{g}$
and let
![]() ${\mathcal{Q}}$
denote the set of conjugacy classes of pairs of elements
${\mathcal{Q}}$
denote the set of conjugacy classes of pairs of elements
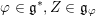 $\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast },Z\in \mathfrak{g}_{\unicode[STIX]{x1D711}}$
such that
$\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast },Z\in \mathfrak{g}_{\unicode[STIX]{x1D711}}$
such that
![]() $\unicode[STIX]{x1D711}$
is nilpotent and
$\unicode[STIX]{x1D711}$
is nilpotent and
![]() $Z$
is rational semi-simple.
$Z$
is rational semi-simple.
Define a map
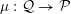 $\unicode[STIX]{x1D707}:{\mathcal{Q}}\rightarrow {\mathcal{P}}$
in the following way: for any
$\unicode[STIX]{x1D707}:{\mathcal{Q}}\rightarrow {\mathcal{P}}$
in the following way: for any
![]() $q\in {\mathcal{Q}}$
choose
$q\in {\mathcal{Q}}$
choose
 $(Z,\unicode[STIX]{x1D711})\in q$
, let
$(Z,\unicode[STIX]{x1D711})\in q$
, let
![]() $h\in \mathfrak{g}_{Z}$
be a neutral element for
$h\in \mathfrak{g}_{Z}$
be a neutral element for
![]() $\unicode[STIX]{x1D711}|_{\mathfrak{g}_{Z}}$
and define
$\unicode[STIX]{x1D711}|_{\mathfrak{g}_{Z}}$
and define
![]() $\unicode[STIX]{x1D707}(q)$
to be the class of the pair
$\unicode[STIX]{x1D707}(q)$
to be the class of the pair
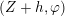 $(Z+h,\unicode[STIX]{x1D711})$
. Then the map
$(Z+h,\unicode[STIX]{x1D711})$
. Then the map
![]() $\unicode[STIX]{x1D707}$
is a well-defined bijection.
$\unicode[STIX]{x1D707}$
is a well-defined bijection.
Proof of Theorem A.
By Lemma 3.0.2 there exists a neutral element
![]() $h$
for
$h$
for
![]() $\unicode[STIX]{x1D711}$
which commutes with
$\unicode[STIX]{x1D711}$
which commutes with
![]() $S$
. Then we have
$S$
. Then we have
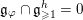 $\mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{g}_{{\geqslant}1}^{h}=0$
. Theorem 3.0.1 applied to the Whittaker pairs
$\mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{g}_{{\geqslant}1}^{h}=0$
. Theorem 3.0.1 applied to the Whittaker pairs
![]() $(h,\unicode[STIX]{x1D711})$
and
$(h,\unicode[STIX]{x1D711})$
and
![]() $(S,\tilde{\unicode[STIX]{x1D711}})$
implies now that there exists a
$(S,\tilde{\unicode[STIX]{x1D711}})$
implies now that there exists a
![]() $G$
-equivariant epimorphism of
$G$
-equivariant epimorphism of
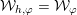 ${\mathcal{W}}_{h,\unicode[STIX]{x1D711}}={\mathcal{W}}_{\unicode[STIX]{x1D711}}$
onto
${\mathcal{W}}_{h,\unicode[STIX]{x1D711}}={\mathcal{W}}_{\unicode[STIX]{x1D711}}$
onto
![]() ${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}$
.◻
${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}$
.◻
In the same way we obtain the following corollary of Theorem 3.0.1 for the case
![]() $\unicode[STIX]{x1D711}=\tilde{\unicode[STIX]{x1D711}}$
.
$\unicode[STIX]{x1D711}=\tilde{\unicode[STIX]{x1D711}}$
.
Corollary 3.0.3. Let
![]() $(S,\unicode[STIX]{x1D711})$
and
$(S,\unicode[STIX]{x1D711})$
and
![]() $(\widetilde{S},\unicode[STIX]{x1D711})$
be two Whittaker pairs with the same nilpotent element and commuting semi-simple elements. If
$(\widetilde{S},\unicode[STIX]{x1D711})$
be two Whittaker pairs with the same nilpotent element and commuting semi-simple elements. If
 $\mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{g}_{{\geqslant}1}^{S}\subset \mathfrak{g}_{{\geqslant}1}^{\widetilde{S}}$
, then there exists a
$\mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{g}_{{\geqslant}1}^{S}\subset \mathfrak{g}_{{\geqslant}1}^{\widetilde{S}}$
, then there exists a
![]() $G$
-equivariant epimorphism of
$G$
-equivariant epimorphism of
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
onto
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
onto
![]() ${\mathcal{W}}_{\widetilde{S},\unicode[STIX]{x1D711}}$
.
${\mathcal{W}}_{\widetilde{S},\unicode[STIX]{x1D711}}$
.
Proof. By Lemma 3.0.2 applied to the group
![]() $G_{\widetilde{S}-S}$
we obtain that there exists a neutral element
$G_{\widetilde{S}-S}$
we obtain that there exists a neutral element
![]() $h$
for
$h$
for
![]() $\unicode[STIX]{x1D711}$
that commutes with
$\unicode[STIX]{x1D711}$
that commutes with
![]() $\widetilde{S}$
and
$\widetilde{S}$
and
![]() $S$
. Thus, the corollary follows from Theorem 3.0.1.◻
$S$
. Thus, the corollary follows from Theorem 3.0.1.◻
This corollary enables one to define a preorder on the set of models corresponding to a fixed nilpotent element
![]() $\unicode[STIX]{x1D711}$
. Let us describe this preorder more explicitly. Choose a neutral element
$\unicode[STIX]{x1D711}$
. Let us describe this preorder more explicitly. Choose a neutral element
![]() $h$
for
$h$
for
![]() $\unicode[STIX]{x1D711}$
and let
$\unicode[STIX]{x1D711}$
and let
![]() $\mathfrak{a}$
be a maximal split Cartan subalgebra in
$\mathfrak{a}$
be a maximal split Cartan subalgebra in
![]() $\mathfrak{g}$
that includes
$\mathfrak{g}$
that includes
![]() $h$
. Choose a root system
$h$
. Choose a root system
![]() $\unicode[STIX]{x1D6F4}$
on
$\unicode[STIX]{x1D6F4}$
on
![]() $\mathfrak{a}$
. By Lemma 3.0.2, if
$\mathfrak{a}$
. By Lemma 3.0.2, if
![]() $(S,\unicode[STIX]{x1D711})$
is any Whittaker pair, then
$(S,\unicode[STIX]{x1D711})$
is any Whittaker pair, then
![]() $S$
is conjugate to
$S$
is conjugate to
![]() $h+Z$
for some
$h+Z$
for some
![]() $Z$
in the stabilizer
$Z$
in the stabilizer
![]() $\mathfrak{a}_{\unicode[STIX]{x1D711}}$
of
$\mathfrak{a}_{\unicode[STIX]{x1D711}}$
of
![]() $\unicode[STIX]{x1D711}$
in
$\unicode[STIX]{x1D711}$
in
![]() $\mathfrak{a}$
.
$\mathfrak{a}$
.
Definition 3.0.4. Let
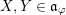 $X,Y\in \mathfrak{a}_{\unicode[STIX]{x1D711}}$
. We say that
$X,Y\in \mathfrak{a}_{\unicode[STIX]{x1D711}}$
. We say that
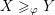 $X\geqslant _{\unicode[STIX]{x1D711}}Y$
if for any
$X\geqslant _{\unicode[STIX]{x1D711}}Y$
if for any
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}$
such that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}$
such that
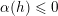 $\unicode[STIX]{x1D6FC}(h)\leqslant 0$
and
$\unicode[STIX]{x1D6FC}(h)\leqslant 0$
and
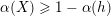 $\unicode[STIX]{x1D6FC}(X)\geqslant 1-\unicode[STIX]{x1D6FC}(h)$
, we have
$\unicode[STIX]{x1D6FC}(X)\geqslant 1-\unicode[STIX]{x1D6FC}(h)$
, we have
 $\unicode[STIX]{x1D6FC}(Y)\geqslant 1-\unicode[STIX]{x1D6FC}(h)$
.
$\unicode[STIX]{x1D6FC}(Y)\geqslant 1-\unicode[STIX]{x1D6FC}(h)$
.
Corollary 3.0.3 immediately implies the following result.
Corollary 3.0.5. If
 $X\geqslant _{\unicode[STIX]{x1D711}}Y$
, then there exists a
$X\geqslant _{\unicode[STIX]{x1D711}}Y$
, then there exists a
![]() $G$
-equivariant epimorphism of
$G$
-equivariant epimorphism of
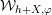 ${\mathcal{W}}_{h+X,\unicode[STIX]{x1D711}}$
onto
${\mathcal{W}}_{h+X,\unicode[STIX]{x1D711}}$
onto
 ${\mathcal{W}}_{h+Y,\unicode[STIX]{x1D711}}$
.
${\mathcal{W}}_{h+Y,\unicode[STIX]{x1D711}}$
.
Remark 3.0.6. For
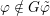 $\unicode[STIX]{x1D711}\notin G\tilde{\unicode[STIX]{x1D711}}$
, the condition on the existence of
$\unicode[STIX]{x1D711}\notin G\tilde{\unicode[STIX]{x1D711}}$
, the condition on the existence of
![]() $h$
cannot be omitted in Theorem 3.0.1. Indeed, let
$h$
cannot be omitted in Theorem 3.0.1. Indeed, let
![]() $\mathbb{F}$
be a
$\mathbb{F}$
be a
![]() $p$
-adic field,
$p$
-adic field,
![]() $\tilde{\unicode[STIX]{x1D711}}$
be a regular nilpotent element in
$\tilde{\unicode[STIX]{x1D711}}$
be a regular nilpotent element in
![]() $\mathfrak{g}_{n}^{\ast }$
and
$\mathfrak{g}_{n}^{\ast }$
and
![]() $\widetilde{S}$
be a neutral element for
$\widetilde{S}$
be a neutral element for
![]() $\tilde{\unicode[STIX]{x1D711}}$
. Let
$\tilde{\unicode[STIX]{x1D711}}$
. Let
![]() $S=\widetilde{S}$
. Then for any non-regular nilpotent orbit we can find a representative
$S=\widetilde{S}$
. Then for any non-regular nilpotent orbit we can find a representative
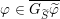 $\unicode[STIX]{x1D711}\in \overline{G_{\widetilde{S}}\widetilde{\unicode[STIX]{x1D711}}}$
. However, for any supercuspidal representation
$\unicode[STIX]{x1D711}\in \overline{G_{\widetilde{S}}\widetilde{\unicode[STIX]{x1D711}}}$
. However, for any supercuspidal representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $G_{n}$
we have
$G_{n}$
we have
 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})=0$
while
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})=0$
while
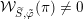 ${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})\neq 0$
.
${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})\neq 0$
.
Remark 3.0.7. The condition
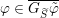 $\unicode[STIX]{x1D711}\in \overline{G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}}$
in Theorem 3.0.1 cannot be replaced by the weaker condition
$\unicode[STIX]{x1D711}\in \overline{G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}}$
in Theorem 3.0.1 cannot be replaced by the weaker condition
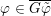 $\unicode[STIX]{x1D711}\in \overline{G\tilde{\unicode[STIX]{x1D711}}}$
. Indeed, let
$\unicode[STIX]{x1D711}\in \overline{G\tilde{\unicode[STIX]{x1D711}}}$
. Indeed, let
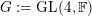 $G:=\text{GL}(4,\mathbb{F})$
, where
$G:=\text{GL}(4,\mathbb{F})$
, where
![]() $\mathbb{F}$
is a
$\mathbb{F}$
is a
![]() $p$
-adic field. Let
$p$
-adic field. Let
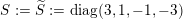 $S:=\widetilde{S}:=\text{diag}(3,1,-1,-3)$
. Let
$S:=\widetilde{S}:=\text{diag}(3,1,-1,-3)$
. Let
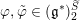 $\unicode[STIX]{x1D711},\tilde{\unicode[STIX]{x1D711}}\in (\mathfrak{g}^{\ast })_{2}^{\widetilde{S}}$
be defined by trace pairing with nilpotent elements in lower-triangular Jordan form with block sizes
$\unicode[STIX]{x1D711},\tilde{\unicode[STIX]{x1D711}}\in (\mathfrak{g}^{\ast })_{2}^{\widetilde{S}}$
be defined by trace pairing with nilpotent elements in lower-triangular Jordan form with block sizes
![]() $(2,2)$
and
$(2,2)$
and
![]() $(3,1)$
in correspondence. Then
$(3,1)$
in correspondence. Then
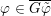 $\unicode[STIX]{x1D711}\in \overline{G\tilde{\unicode[STIX]{x1D711}}}$
but
$\unicode[STIX]{x1D711}\in \overline{G\tilde{\unicode[STIX]{x1D711}}}$
but
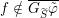 $f\notin \overline{G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}}$
. Let
$f\notin \overline{G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}}$
. Let
![]() $\unicode[STIX]{x1D712}$
be a character of
$\unicode[STIX]{x1D712}$
be a character of
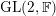 $\text{GL}(2,\mathbb{F})$
,
$\text{GL}(2,\mathbb{F})$
,
![]() $\unicode[STIX]{x1D70E}$
be an irreducible cuspidal representation of
$\unicode[STIX]{x1D70E}$
be an irreducible cuspidal representation of
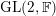 $\text{GL}(2,\mathbb{F})$
and
$\text{GL}(2,\mathbb{F})$
and
 $\unicode[STIX]{x1D70B}:=\unicode[STIX]{x1D712}\times \unicode[STIX]{x1D70E}\in {\mathcal{M}}(G)$
be their Bernstein–Zelevinsky product. Then the spaces
$\unicode[STIX]{x1D70B}:=\unicode[STIX]{x1D712}\times \unicode[STIX]{x1D70E}\in {\mathcal{M}}(G)$
be their Bernstein–Zelevinsky product. Then the spaces
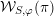 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
and
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
and
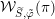 ${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})$
can be expressed through the Bernstein–Zelevinsky derivatives (see [Reference Bernstein and ZelevinskyBZ77]) in the following way:
${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})$
can be expressed through the Bernstein–Zelevinsky derivatives (see [Reference Bernstein and ZelevinskyBZ77]) in the following way:
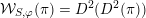 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})=D^{2}(D^{2}(\unicode[STIX]{x1D70B}))$
and
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})=D^{2}(D^{2}(\unicode[STIX]{x1D70B}))$
and
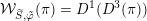 ${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})=D^{1}(D^{3}(\unicode[STIX]{x1D70B}))$
. We have
${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})=D^{1}(D^{3}(\unicode[STIX]{x1D70B}))$
. We have
 $$\begin{eqnarray}D^{1}(\unicode[STIX]{x1D70E})=0,\quad D^{2}(\unicode[STIX]{x1D70E})=\mathbb{C},\quad D^{1}(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}|_{\text{GL}(1,\mathbb{Q}_{p})},\quad D^{1}(D^{1}(\unicode[STIX]{x1D712}))=\mathbb{C},\quad D^{2}(\unicode[STIX]{x1D712})=0,\end{eqnarray}$$
$$\begin{eqnarray}D^{1}(\unicode[STIX]{x1D70E})=0,\quad D^{2}(\unicode[STIX]{x1D70E})=\mathbb{C},\quad D^{1}(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}|_{\text{GL}(1,\mathbb{Q}_{p})},\quad D^{1}(D^{1}(\unicode[STIX]{x1D712}))=\mathbb{C},\quad D^{2}(\unicode[STIX]{x1D712})=0,\end{eqnarray}$$
and by the Leibnitz rule for Bernstein–Zelevinsky derivatives
 $$\begin{eqnarray}D^{2}(\unicode[STIX]{x1D70B})=\unicode[STIX]{x1D712},\quad D^{2}(D^{2}(\unicode[STIX]{x1D70B}))=0,\quad D^{3}(\unicode[STIX]{x1D70B})=\unicode[STIX]{x1D712}|_{\text{GL}(1,\mathbb{Q}_{p})},\quad D^{1}(D^{3}(\unicode[STIX]{x1D70B}))=\mathbb{C},\end{eqnarray}$$
$$\begin{eqnarray}D^{2}(\unicode[STIX]{x1D70B})=\unicode[STIX]{x1D712},\quad D^{2}(D^{2}(\unicode[STIX]{x1D70B}))=0,\quad D^{3}(\unicode[STIX]{x1D70B})=\unicode[STIX]{x1D712}|_{\text{GL}(1,\mathbb{Q}_{p})},\quad D^{1}(D^{3}(\unicode[STIX]{x1D70B}))=\mathbb{C},\end{eqnarray}$$
and thus
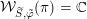 ${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})=\mathbb{C}$
while
${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})=\mathbb{C}$
while
 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})=0$
.
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})=0$
.
3.1 Proof of Lemma 3.0.2
We will need the following lemma.
Lemma 3.1.1. Let
![]() $(f,h,e)$
be an
$(f,h,e)$
be an
![]() $\mathfrak{sl}_{2}$
-triple in
$\mathfrak{sl}_{2}$
-triple in
![]() $\mathfrak{g}$
, let
$\mathfrak{g}$
, let
![]() $L$
be its centralizer in
$L$
be its centralizer in
![]() $G$
and let
$G$
and let
![]() $\mathfrak{l}$
be its centralizer in
$\mathfrak{l}$
be its centralizer in
![]() $\mathfrak{g}$
. Let
$\mathfrak{g}$
. Let
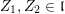 $Z_{1},Z_{2}\in \mathfrak{l}$
and suppose that
$Z_{1},Z_{2}\in \mathfrak{l}$
and suppose that
![]() $h+Z_{1}$
is conjugate to
$h+Z_{1}$
is conjugate to
![]() $h+Z_{2}$
by an element of
$h+Z_{2}$
by an element of
![]() $G_{f}$
. Then
$G_{f}$
. Then
![]() $Z_{1}$
is conjugate to
$Z_{1}$
is conjugate to
![]() $Z_{2}$
by an element of
$Z_{2}$
by an element of
![]() $L$
.
$L$
.
Proof. Note the Levi decomposition
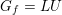 $G_{f}=LU$
, where
$G_{f}=LU$
, where
![]() $U$
is the nilradical of
$U$
is the nilradical of
![]() $G_{f}$
. It is enough to show that if
$G_{f}$
. It is enough to show that if
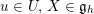 $u\in U,\,X\in \mathfrak{g}_{h}$
and
$u\in U,\,X\in \mathfrak{g}_{h}$
and
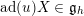 $\text{ad}(u)X\in \mathfrak{g}_{h}$
, then
$\text{ad}(u)X\in \mathfrak{g}_{h}$
, then
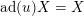 $\text{ad}(u)X=X$
. This holds since
$\text{ad}(u)X=X$
. This holds since
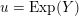 $u=\text{Exp}(Y)$
for some
$u=\text{Exp}(Y)$
for some
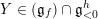 $Y\in (\mathfrak{g}_{f})\cap \mathfrak{g}_{{<}0}^{h}$
and
$Y\in (\mathfrak{g}_{f})\cap \mathfrak{g}_{{<}0}^{h}$
and
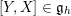 $[Y,X]\in \mathfrak{g}_{h}$
.◻
$[Y,X]\in \mathfrak{g}_{h}$
.◻
Proof of Lemma 3.0.2.
We choose a non-degenerate conjugation-invariant symmetric bilinear form on
![]() $\mathfrak{g}$
and use it to identify
$\mathfrak{g}$
and use it to identify
![]() $\mathfrak{g}$
with
$\mathfrak{g}$
with
![]() $\mathfrak{g}^{\ast }$
. Thus, instead of
$\mathfrak{g}^{\ast }$
. Thus, instead of
![]() $\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
we will consider
$\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
we will consider
![]() $f\in \mathfrak{g}$
.
$f\in \mathfrak{g}$
.
To see that
![]() $\unicode[STIX]{x1D707}$
is well-defined, let
$\unicode[STIX]{x1D707}$
is well-defined, let
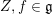 $Z,f\in \mathfrak{g}$
. Let
$Z,f\in \mathfrak{g}$
. Let
![]() $(f,h,e)$
be an
$(f,h,e)$
be an
![]() $\mathfrak{sl}_{2}$
-triple in
$\mathfrak{sl}_{2}$
-triple in
![]() $\mathfrak{g}_{Z}$
. Note that any two choices of such a triple are conjugate by
$\mathfrak{g}_{Z}$
. Note that any two choices of such a triple are conjugate by
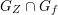 $G_{Z}\cap G_{f}$
. Note also that for any
$G_{Z}\cap G_{f}$
. Note also that for any
![]() $g\in G$
,
$g\in G$
,
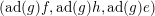 $(\text{ad}(g)f,\text{ad}(g)h,\text{ad}(g)e)$
is an
$(\text{ad}(g)f,\text{ad}(g)h,\text{ad}(g)e)$
is an
![]() $\mathfrak{sl}_{2}$
-triple in
$\mathfrak{sl}_{2}$
-triple in
![]() $\mathfrak{g}_{\text{ad}(g)Z}$
, and
$\mathfrak{g}_{\text{ad}(g)Z}$
, and
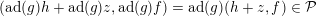 $(\text{ad}(g)h+\text{ad}(g)z,\text{ad}(g)f)=\text{ad}(g)(h+z,f)\in {\mathcal{P}}$
. Thus
$(\text{ad}(g)h+\text{ad}(g)z,\text{ad}(g)f)=\text{ad}(g)(h+z,f)\in {\mathcal{P}}$
. Thus
![]() $\unicode[STIX]{x1D707}$
is well-defined.
$\unicode[STIX]{x1D707}$
is well-defined.
To see that
![]() $\unicode[STIX]{x1D707}$
is onto, let
$\unicode[STIX]{x1D707}$
is onto, let
![]() $c\in {\mathcal{P}}$
and
$c\in {\mathcal{P}}$
and
 $(S,f)\in c$
. Fix an embedding
$(S,f)\in c$
. Fix an embedding
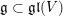 $\mathfrak{g}\subset \mathfrak{gl}(V)$
. Let us show that there exists a basis for
$\mathfrak{g}\subset \mathfrak{gl}(V)$
. Let us show that there exists a basis for
![]() $V$
in which
$V$
in which
![]() $S$
is diagonal and
$S$
is diagonal and
![]() $f$
is in Jordan form. First of all let
$f$
is in Jordan form. First of all let
![]() $\{\unicode[STIX]{x1D706}_{i}\}_{i=1}^{k}$
be all the eigenvalues of
$\{\unicode[STIX]{x1D706}_{i}\}_{i=1}^{k}$
be all the eigenvalues of
![]() $S$
, ordered such that
$S$
, ordered such that
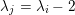 $\unicode[STIX]{x1D706}_{j}=\unicode[STIX]{x1D706}_{i}-2$
only if
$\unicode[STIX]{x1D706}_{j}=\unicode[STIX]{x1D706}_{i}-2$
only if
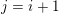 $j=i+1$
, and let
$j=i+1$
, and let
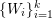 $\{W_{i}\}_{i=1}^{k}$
be the corresponding eigenspaces. Then
$\{W_{i}\}_{i=1}^{k}$
be the corresponding eigenspaces. Then
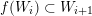 $f(W_{i})\subset W_{i+1}$
, and thus
$f(W_{i})\subset W_{i+1}$
, and thus
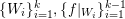 $\{W_{i}\}_{i=1}^{k},\{f|_{W_{i}}\}_{i=1}^{k-1}$
form a representation of a type A quiver. By [Reference GabrielGab72] (see also [Reference Bernstein, Gel’fand and PonomarevBGP73, Theorem 3.1(2)]), any such representation is a direct sum of indecomposable representations in which all of the spaces have dimensions 0 or 1. Each of these representations gives a Jordan chain for
$\{W_{i}\}_{i=1}^{k},\{f|_{W_{i}}\}_{i=1}^{k-1}$
form a representation of a type A quiver. By [Reference GabrielGab72] (see also [Reference Bernstein, Gel’fand and PonomarevBGP73, Theorem 3.1(2)]), any such representation is a direct sum of indecomposable representations in which all of the spaces have dimensions 0 or 1. Each of these representations gives a Jordan chain for
![]() $f$
. Then the union of these chains is the required basis. With respect to this basis
$f$
. Then the union of these chains is the required basis. With respect to this basis
![]() $f$
is in Jordan form and
$f$
is in Jordan form and
![]() $S$
is diagonal. Thus there exists a diagonal neutral element
$S$
is diagonal. Thus there exists a diagonal neutral element
![]() $-h^{\prime }$
for
$-h^{\prime }$
for
![]() $f$
in
$f$
in
![]() $\mathfrak{gl}(V)$
, which then commutes with
$\mathfrak{gl}(V)$
, which then commutes with
![]() $S$
. Since
$S$
. Since
![]() $\mathfrak{g}$
is reductive, there exists a
$\mathfrak{g}$
is reductive, there exists a
![]() $\mathfrak{g}$
-module projection
$\mathfrak{g}$
-module projection
 $p:\mathfrak{gl}(V)\,{\twoheadrightarrow}\,\mathfrak{g}$
. Let
$p:\mathfrak{gl}(V)\,{\twoheadrightarrow}\,\mathfrak{g}$
. Let
 $h:=p(h^{\prime })$
. Then
$h:=p(h^{\prime })$
. Then
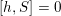 $[h,S]=0$
. Moreover,
$[h,S]=0$
. Moreover,
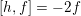 $[h,f]=-2f$
and
$[h,f]=-2f$
and
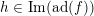 $h\in \text{Im}(\text{ad}(f))$
and thus, by Lemma 2.2.1,
$h\in \text{Im}(\text{ad}(f))$
and thus, by Lemma 2.2.1,
![]() $-h$
is a neutral element for
$-h$
is a neutral element for
![]() $f$
. Thus,
$f$
. Thus,
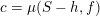 $c=\unicode[STIX]{x1D707}(S-h,f)$
.
$c=\unicode[STIX]{x1D707}(S-h,f)$
.
It is left to show that
![]() $\unicode[STIX]{x1D707}$
is injective. Let
$\unicode[STIX]{x1D707}$
is injective. Let
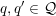 $q,q^{\prime }\in {\mathcal{Q}}$
such that
$q,q^{\prime }\in {\mathcal{Q}}$
such that
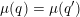 $\unicode[STIX]{x1D707}(q)=\unicode[STIX]{x1D707}(q^{\prime })$
, and let
$\unicode[STIX]{x1D707}(q)=\unicode[STIX]{x1D707}(q^{\prime })$
, and let
![]() $(Z,f)$
and
$(Z,f)$
and
![]() $(Z^{\prime },f^{\prime })$
be their representatives. Then there exist
$(Z^{\prime },f^{\prime })$
be their representatives. Then there exist
![]() $\mathfrak{sl}_{2}$
-triples
$\mathfrak{sl}_{2}$
-triples
![]() $(f,h,e)$
in
$(f,h,e)$
in
![]() $\mathfrak{g}_{Z}$
and
$\mathfrak{g}_{Z}$
and
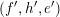 $(f^{\prime },h^{\prime },e^{\prime })$
in
$(f^{\prime },h^{\prime },e^{\prime })$
in
![]() $\mathfrak{g}_{Z^{\prime }}$
, and
$\mathfrak{g}_{Z^{\prime }}$
, and
![]() $g\in G$
such that
$g\in G$
such that
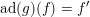 $\text{ad}(g)(f)=f^{\prime }$
and
$\text{ad}(g)(f)=f^{\prime }$
and
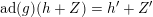 $\text{ad}(g)(h+Z)=h^{\prime }+Z^{\prime }$
. Note that
$\text{ad}(g)(h+Z)=h^{\prime }+Z^{\prime }$
. Note that
 $(f^{\prime },\text{ad}(g)h,\text{ad}(g)e)$
is an
$(f^{\prime },\text{ad}(g)h,\text{ad}(g)e)$
is an
![]() $\mathfrak{sl}_{2}$
-triple and thus
$\mathfrak{sl}_{2}$
-triple and thus
![]() $\text{ad}(g)h$
and
$\text{ad}(g)h$
and
![]() $h^{\prime }$
are conjugate by
$h^{\prime }$
are conjugate by
![]() $G_{f}$
. Thus, we can assume that
$G_{f}$
. Thus, we can assume that
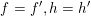 $f=f^{\prime },h=h^{\prime }$
, and
$f=f^{\prime },h=h^{\prime }$
, and
![]() $h+Z$
is conjugate to
$h+Z$
is conjugate to
![]() $h+Z^{\prime }$
by
$h+Z^{\prime }$
by
![]() $G_{f}$
. By Lemma 3.1.1 this implies that
$G_{f}$
. By Lemma 3.1.1 this implies that
![]() $Z$
is conjugate to
$Z$
is conjugate to
![]() $Z^{\prime }$
by
$Z^{\prime }$
by
![]() $G_{f}$
and thus
$G_{f}$
and thus
![]() $(Z,f)$
is conjugate to
$(Z,f)$
is conjugate to
![]() $(Z^{\prime },f^{\prime })$
.◻
$(Z^{\prime },f^{\prime })$
.◻
3.2 Proof of Theorem 3.0.1
Let
![]() $\unicode[STIX]{x1D714}$
denote the anti-symmetric form
$\unicode[STIX]{x1D714}$
denote the anti-symmetric form
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}$
on
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}$
on
![]() $\mathfrak{g}$
defined by
$\mathfrak{g}$
defined by
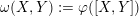 $\unicode[STIX]{x1D714}(X,Y):=\unicode[STIX]{x1D711}([X,Y])$
.
$\unicode[STIX]{x1D714}(X,Y):=\unicode[STIX]{x1D711}([X,Y])$
.
Our proof is based on the following lemma, which is in the spirit of [Reference Ginzburg, Rallis and SoudryGRS99, Lemma 2.2], [Reference Ginzburg, Rallis and SoudryGRS11, Lemma 7.1] or [Reference Lapid and MaoLM15a, Lemma A.1].
Lemma 3.2.1. Let
![]() $\mathfrak{l},\mathfrak{r}\subset \mathfrak{g}$
be nilpotent subalgebras such that
$\mathfrak{l},\mathfrak{r}\subset \mathfrak{g}$
be nilpotent subalgebras such that
 $[\mathfrak{l},\mathfrak{r}]\subset \mathfrak{l}\cap \mathfrak{r}$
,
$[\mathfrak{l},\mathfrak{r}]\subset \mathfrak{l}\cap \mathfrak{r}$
,
![]() $\unicode[STIX]{x1D714}|_{\mathfrak{l}}=0$
,
$\unicode[STIX]{x1D714}|_{\mathfrak{l}}=0$
,
![]() $\unicode[STIX]{x1D714}|_{\mathfrak{r}}=0$
and the radical of
$\unicode[STIX]{x1D714}|_{\mathfrak{r}}=0$
and the radical of
![]() $\unicode[STIX]{x1D714}|_{\mathfrak{l}+\mathfrak{r}}$
is
$\unicode[STIX]{x1D714}|_{\mathfrak{l}+\mathfrak{r}}$
is
![]() $\mathfrak{l}\cap \mathfrak{r}$
. Then
$\mathfrak{l}\cap \mathfrak{r}$
. Then
![]() $\mathfrak{l}+\mathfrak{r}$
is a nilpotent Lie algebra and
$\mathfrak{l}+\mathfrak{r}$
is a nilpotent Lie algebra and
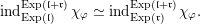 $$\begin{eqnarray}\text{ind}_{\text{Exp}(\mathfrak{l})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{ind}_{\text{Exp}(\mathfrak{l})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}.\end{eqnarray}$$
Proof. If
![]() $\unicode[STIX]{x1D711}=0$
, then
$\unicode[STIX]{x1D711}=0$
, then
![]() $\unicode[STIX]{x1D714}=0$
, thus
$\unicode[STIX]{x1D714}=0$
, thus
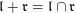 $\mathfrak{l}+\mathfrak{r}=\mathfrak{l}\cap \mathfrak{r}$
,
$\mathfrak{l}+\mathfrak{r}=\mathfrak{l}\cap \mathfrak{r}$
,
![]() $\mathfrak{l}=\mathfrak{r}$
and there is nothing to prove. Now suppose
$\mathfrak{l}=\mathfrak{r}$
and there is nothing to prove. Now suppose
![]() $\unicode[STIX]{x1D711}\neq 0$
and denote
$\unicode[STIX]{x1D711}\neq 0$
and denote
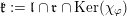 $\mathfrak{k}:=\mathfrak{l}\cap \mathfrak{r}\cap \text{Ker}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})$
. Then
$\mathfrak{k}:=\mathfrak{l}\cap \mathfrak{r}\cap \text{Ker}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})$
. Then
 $\text{Exp}(\mathfrak{l}+\mathfrak{r})/\text{Exp}(\mathfrak{k})$
is the Heisenberg group corresponding to the symplectic form induced by
$\text{Exp}(\mathfrak{l}+\mathfrak{r})/\text{Exp}(\mathfrak{k})$
is the Heisenberg group corresponding to the symplectic form induced by
![]() $\unicode[STIX]{x1D714}$
on the space
$\unicode[STIX]{x1D714}$
on the space
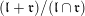 $(\mathfrak{l}+\mathfrak{r})/(\mathfrak{l}\cap \mathfrak{r})$
. Since
$(\mathfrak{l}+\mathfrak{r})/(\mathfrak{l}\cap \mathfrak{r})$
. Since
![]() $\mathfrak{l}/(\mathfrak{l}\cap \mathfrak{r})$
and
$\mathfrak{l}/(\mathfrak{l}\cap \mathfrak{r})$
and
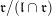 $\mathfrak{r}/(\mathfrak{l}\cap \mathfrak{r})$
are Lagrangian subspaces, the representations
$\mathfrak{r}/(\mathfrak{l}\cap \mathfrak{r})$
are Lagrangian subspaces, the representations
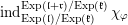 $\text{ind}_{\text{Exp}(\mathfrak{l})/\text{Exp}(\mathfrak{k})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})/\text{Exp}(\mathfrak{k})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
and
$\text{ind}_{\text{Exp}(\mathfrak{l})/\text{Exp}(\mathfrak{k})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})/\text{Exp}(\mathfrak{k})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
and
 $\text{ind}_{\text{Exp}(\mathfrak{r})/\text{Exp}(\mathfrak{k})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})/\text{Exp}(\mathfrak{k})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
are both isomorphic to the oscillator representation
$\text{ind}_{\text{Exp}(\mathfrak{r})/\text{Exp}(\mathfrak{k})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})/\text{Exp}(\mathfrak{k})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
are both isomorphic to the oscillator representation
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
of
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
of
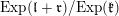 $\text{Exp}(\mathfrak{l}+\mathfrak{r})/\text{Exp}(\mathfrak{k})$
with central character defined by
$\text{Exp}(\mathfrak{l}+\mathfrak{r})/\text{Exp}(\mathfrak{k})$
with central character defined by
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. Since
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
. Since
![]() $\text{Exp}(\mathfrak{k})$
acts trivially on
$\text{Exp}(\mathfrak{k})$
acts trivially on
 $\text{ind}_{\text{Exp}(\mathfrak{l})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
and
$\text{ind}_{\text{Exp}(\mathfrak{l})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
and
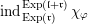 $\text{ind}_{\text{Exp}(\mathfrak{r})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
, we obtain that they are both isomorphic to the trivial extension of
$\text{ind}_{\text{Exp}(\mathfrak{r})}^{\text{Exp}(\mathfrak{l}+\mathfrak{r})}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
, we obtain that they are both isomorphic to the trivial extension of
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
to
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
to
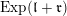 $\text{Exp}(\mathfrak{l}+\mathfrak{r})$
.◻
$\text{Exp}(\mathfrak{l}+\mathfrak{r})$
.◻
Remark 3.2.2. By induction by stages we obtain
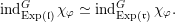 $\text{ind}_{\text{Exp}(\mathfrak{l})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}.$
Observe that this isomorphism can be realized explicitly as an integral transform: given
$\text{ind}_{\text{Exp}(\mathfrak{l})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}.$
Observe that this isomorphism can be realized explicitly as an integral transform: given
 $f\in \text{ind}_{\text{Exp}(\mathfrak{l})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
we can define
$f\in \text{ind}_{\text{Exp}(\mathfrak{l})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
we can define
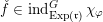 $\check{f}\in \text{ind}_{\text{Exp}(\mathfrak{r})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
simply by setting
$\check{f}\in \text{ind}_{\text{Exp}(\mathfrak{r})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
simply by setting
 $$\begin{eqnarray}\check{f}(g)=\int _{\text{Exp}(\mathfrak{l}\cap \mathfrak{r})\backslash \text{Exp}(\mathfrak{r})}f(ng)\,dn.\end{eqnarray}$$
$$\begin{eqnarray}\check{f}(g)=\int _{\text{Exp}(\mathfrak{l}\cap \mathfrak{r})\backslash \text{Exp}(\mathfrak{r})}f(ng)\,dn.\end{eqnarray}$$
Then the previous results imply that the map
![]() $f\mapsto \check{f}$
defines an isomorphism between these two spaces.
$f\mapsto \check{f}$
defines an isomorphism between these two spaces.
In the course of our proof we will make several choices and introduce some notation. The reader is welcome to track those on Examples 3.2.11 and 3.2.12 below.
Let
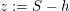 $z:=S-h$
and
$z:=S-h$
and
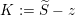 $K:=\widetilde{S}-z$
. Choose a symmetric bilinear non-degenerate
$K:=\widetilde{S}-z$
. Choose a symmetric bilinear non-degenerate
![]() $G$
-invariant form on
$G$
-invariant form on
![]() $\mathfrak{g}$
and let
$\mathfrak{g}$
and let
![]() $f\in \mathfrak{g}$
correspond to
$f\in \mathfrak{g}$
correspond to
![]() $\unicode[STIX]{x1D711}$
using this form. Let
$\unicode[STIX]{x1D711}$
using this form. Let
![]() $e$
be the nil-positive element for
$e$
be the nil-positive element for
![]() $h$
and
$h$
and
![]() $f$
. Then
$f$
. Then
 $e\in \mathfrak{a}:=\mathfrak{g}_{z}$
. Consider the embedding
$e\in \mathfrak{a}:=\mathfrak{g}_{z}$
. Consider the embedding
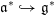 $\mathfrak{a}^{\ast }{\hookrightarrow}\mathfrak{g}^{\ast }$
corresponding to the bilinear form on
$\mathfrak{a}^{\ast }{\hookrightarrow}\mathfrak{g}^{\ast }$
corresponding to the bilinear form on
![]() $\mathfrak{g}$
. Let
$\mathfrak{g}$
. Let
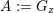 $A:=G_{z}$
.
$A:=G_{z}$
.
Lemma 3.2.3. There exists
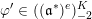 $\unicode[STIX]{x1D711}^{\prime }\in ((\mathfrak{a}^{\ast })^{e})_{-2}^{K}$
such that
$\unicode[STIX]{x1D711}^{\prime }\in ((\mathfrak{a}^{\ast })^{e})_{-2}^{K}$
such that
 $\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }\in G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}$
.
$\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }\in G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}$
.
Proof. Note that
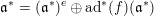 $\mathfrak{a}^{\ast }=(\mathfrak{a}^{\ast })^{e}\oplus \text{ad}^{\ast }(f)(\mathfrak{a}^{\ast })$
. Since
$\mathfrak{a}^{\ast }=(\mathfrak{a}^{\ast })^{e}\oplus \text{ad}^{\ast }(f)(\mathfrak{a}^{\ast })$
. Since
![]() $K$
preserves both summands we get
$K$
preserves both summands we get
 $$\begin{eqnarray}(\mathfrak{a}^{\ast })_{-2}^{K}=((\mathfrak{a}^{\ast })^{e})_{-2}^{K}\oplus (\text{ad}^{\ast }(f)(\mathfrak{a}))_{-2}^{K}=((\mathfrak{a}^{\ast })^{e})_{-2}^{K}\oplus \text{ad}^{\ast }(\mathfrak{a}_{K})(\unicode[STIX]{x1D711}).\end{eqnarray}$$
$$\begin{eqnarray}(\mathfrak{a}^{\ast })_{-2}^{K}=((\mathfrak{a}^{\ast })^{e})_{-2}^{K}\oplus (\text{ad}^{\ast }(f)(\mathfrak{a}))_{-2}^{K}=((\mathfrak{a}^{\ast })^{e})_{-2}^{K}\oplus \text{ad}^{\ast }(\mathfrak{a}_{K})(\unicode[STIX]{x1D711}).\end{eqnarray}$$
Consider the map
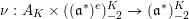 $\unicode[STIX]{x1D708}:A_{K}\times ((\mathfrak{a}^{\ast })^{e})_{-2}^{K}\rightarrow (\mathfrak{a}^{\ast })_{-2}^{K}$
given by
$\unicode[STIX]{x1D708}:A_{K}\times ((\mathfrak{a}^{\ast })^{e})_{-2}^{K}\rightarrow (\mathfrak{a}^{\ast })_{-2}^{K}$
given by
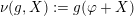 $\unicode[STIX]{x1D708}(g,X):=g(\unicode[STIX]{x1D711}+X)$
. Note that the differential of
$\unicode[STIX]{x1D708}(g,X):=g(\unicode[STIX]{x1D711}+X)$
. Note that the differential of
![]() $\unicode[STIX]{x1D708}$
at the point
$\unicode[STIX]{x1D708}$
at the point
![]() $(1,0)$
is onto, and thus the image of
$(1,0)$
is onto, and thus the image of
![]() $\unicode[STIX]{x1D708}$
contains an open neighborhood of
$\unicode[STIX]{x1D708}$
contains an open neighborhood of
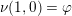 $\unicode[STIX]{x1D708}(1,0)=\unicode[STIX]{x1D711}$
. Since
$\unicode[STIX]{x1D708}(1,0)=\unicode[STIX]{x1D711}$
. Since
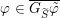 $\unicode[STIX]{x1D711}\in \overline{G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}}$
, the image of
$\unicode[STIX]{x1D711}\in \overline{G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}}$
, the image of
![]() $\unicode[STIX]{x1D708}$
intersects the orbit
$\unicode[STIX]{x1D708}$
intersects the orbit
![]() $G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}$
.◻
$G_{\widetilde{S}}\tilde{\unicode[STIX]{x1D711}}$
.◻
Let
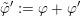 $\tilde{\unicode[STIX]{x1D711}}^{\prime }:=\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }$
. Let
$\tilde{\unicode[STIX]{x1D711}}^{\prime }:=\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }$
. Let
![]() $i$
denote the smallest of the
$i$
denote the smallest of the
![]() $h$
-weights of
$h$
-weights of
![]() $\unicode[STIX]{x1D711}^{\prime }$
. If
$\unicode[STIX]{x1D711}^{\prime }$
. If
![]() $\unicode[STIX]{x1D711}^{\prime }=0$
we take
$\unicode[STIX]{x1D711}^{\prime }=0$
we take
![]() $i$
to be 0. Note that
$i$
to be 0. Note that
![]() $i$
is always non-negative.
$i$
is always non-negative.
Lemma 3.2.4. If
![]() $\unicode[STIX]{x1D711}^{\prime }\neq 0$
, then there exists
$\unicode[STIX]{x1D711}^{\prime }\neq 0$
, then there exists
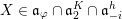 $X\in \mathfrak{a}_{\unicode[STIX]{x1D711}}\cap \mathfrak{a}_{2}^{K}\cap \mathfrak{a}_{-i}^{h}$
such that
$X\in \mathfrak{a}_{\unicode[STIX]{x1D711}}\cap \mathfrak{a}_{2}^{K}\cap \mathfrak{a}_{-i}^{h}$
such that
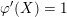 $\unicode[STIX]{x1D711}^{\prime }(X)=1$
.
$\unicode[STIX]{x1D711}^{\prime }(X)=1$
.
Proof. Let
![]() $\unicode[STIX]{x1D711}_{i}^{\prime }$
be the component of
$\unicode[STIX]{x1D711}_{i}^{\prime }$
be the component of
![]() $\unicode[STIX]{x1D711}^{\prime }$
of weight
$\unicode[STIX]{x1D711}^{\prime }$
of weight
![]() $i$
. There exists
$i$
. There exists
![]() $Y\in \mathfrak{a}$
with
$Y\in \mathfrak{a}$
with
 $\unicode[STIX]{x1D711}_{i}^{\prime }(Y)=1$
. Let
$\unicode[STIX]{x1D711}_{i}^{\prime }(Y)=1$
. Let
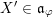 $X^{\prime }\in \mathfrak{a}_{\unicode[STIX]{x1D711}}$
be the component of
$X^{\prime }\in \mathfrak{a}_{\unicode[STIX]{x1D711}}$
be the component of
![]() $Y$
in the decomposition
$Y$
in the decomposition
 $\mathfrak{a}=[e,\mathfrak{a}]\oplus \mathfrak{a}_{\unicode[STIX]{x1D711}}$
. Since
$\mathfrak{a}=[e,\mathfrak{a}]\oplus \mathfrak{a}_{\unicode[STIX]{x1D711}}$
. Since
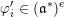 $\unicode[STIX]{x1D711}_{i}^{\prime }\in (\mathfrak{a}^{\ast })^{e}$
,
$\unicode[STIX]{x1D711}_{i}^{\prime }\in (\mathfrak{a}^{\ast })^{e}$
,
![]() $\unicode[STIX]{x1D711}_{i}^{\prime }$
vanishes on
$\unicode[STIX]{x1D711}_{i}^{\prime }$
vanishes on
![]() $[e,\mathfrak{a}]$
and thus
$[e,\mathfrak{a}]$
and thus
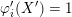 $\unicode[STIX]{x1D711}_{i}^{\prime }(X^{\prime })=1$
. Decompose
$\unicode[STIX]{x1D711}_{i}^{\prime }(X^{\prime })=1$
. Decompose
![]() $\mathfrak{a}_{\unicode[STIX]{x1D711}}$
to joint eigenspaces of the commuting semi-simple operators
$\mathfrak{a}_{\unicode[STIX]{x1D711}}$
to joint eigenspaces of the commuting semi-simple operators
![]() $h$
and
$h$
and
![]() $K$
and let
$K$
and let
![]() $X$
be the component of
$X$
be the component of
![]() $X^{\prime }$
in
$X^{\prime }$
in
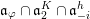 $\mathfrak{a}_{\unicode[STIX]{x1D711}}\cap \mathfrak{a}_{2}^{K}\cap \mathfrak{a}_{-i}^{h}$
. Then
$\mathfrak{a}_{\unicode[STIX]{x1D711}}\cap \mathfrak{a}_{2}^{K}\cap \mathfrak{a}_{-i}^{h}$
. Then
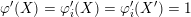 $\unicode[STIX]{x1D711}^{\prime }(X)=\unicode[STIX]{x1D711}_{i}^{\prime }(X)=\unicode[STIX]{x1D711}_{i}^{\prime }(X^{\prime })=1$
.◻
$\unicode[STIX]{x1D711}^{\prime }(X)=\unicode[STIX]{x1D711}_{i}^{\prime }(X)=\unicode[STIX]{x1D711}_{i}^{\prime }(X^{\prime })=1$
.◻
Let
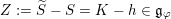 $Z:=\widetilde{S}-S=K-h\in \mathfrak{g}_{\unicode[STIX]{x1D711}}$
. For any rational number
$Z:=\widetilde{S}-S=K-h\in \mathfrak{g}_{\unicode[STIX]{x1D711}}$
. For any rational number
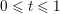 $0\leqslant t\leqslant 1$
define
$0\leqslant t\leqslant 1$
define
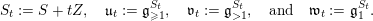 $$\begin{eqnarray}S_{t}:=S+tZ,\quad \mathfrak{u}_{t}:=\mathfrak{g}_{{\geqslant}1}^{S_{t}},\quad \mathfrak{v}_{t}:=\mathfrak{g}_{{>}1}^{S_{t}},\quad \text{and}\quad \mathfrak{w}_{t}:=\mathfrak{g}_{1}^{S_{t}}.\end{eqnarray}$$
$$\begin{eqnarray}S_{t}:=S+tZ,\quad \mathfrak{u}_{t}:=\mathfrak{g}_{{\geqslant}1}^{S_{t}},\quad \mathfrak{v}_{t}:=\mathfrak{g}_{{>}1}^{S_{t}},\quad \text{and}\quad \mathfrak{w}_{t}:=\mathfrak{g}_{1}^{S_{t}}.\end{eqnarray}$$
Definition 3.2.5. We call
![]() $t$
regular if
$t$
regular if
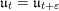 $\mathfrak{u}_{t}=\mathfrak{u}_{t+\unicode[STIX]{x1D700}}$
for any small enough
$\mathfrak{u}_{t}=\mathfrak{u}_{t+\unicode[STIX]{x1D700}}$
for any small enough
![]() $\unicode[STIX]{x1D700}\in \mathbb{Q}$
, or in other words
$\unicode[STIX]{x1D700}\in \mathbb{Q}$
, or in other words
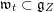 $\mathfrak{w}_{t}\subset \mathfrak{g}_{Z}$
. If
$\mathfrak{w}_{t}\subset \mathfrak{g}_{Z}$
. If
![]() $t$
is not regular we call it critical. For convenience, we will say that 0 is critical and 1 is regular.
$t$
is not regular we call it critical. For convenience, we will say that 0 is critical and 1 is regular.
Note that there are only finitely many critical numbers.
Lemma 3.2.6. The following results hold:
-
(i) the form
 $\unicode[STIX]{x1D714}$
is
$\unicode[STIX]{x1D714}$
is
 $\text{ad}(Z)$
-invariant;
$\text{ad}(Z)$
-invariant; -
(ii)
 $\text{Ker}\,\unicode[STIX]{x1D714}=\mathfrak{g}_{\unicode[STIX]{x1D711}}=\mathfrak{g}^{f}\subset \mathfrak{g}_{{\leqslant}0}^{h}$
;
$\text{Ker}\,\unicode[STIX]{x1D714}=\mathfrak{g}_{\unicode[STIX]{x1D711}}=\mathfrak{g}^{f}\subset \mathfrak{g}_{{\leqslant}0}^{h}$
; -
(iii)
 $\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{w}_{t}})=\text{Ker}(\unicode[STIX]{x1D714})\cap \mathfrak{w}_{t}$
;
$\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{w}_{t}})=\text{Ker}(\unicode[STIX]{x1D714})\cap \mathfrak{w}_{t}$
; -
(iv)
 $\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{u}_{t}})=\mathfrak{v}_{t}\oplus \text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{w}_{t}})$
;
$\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{u}_{t}})=\mathfrak{v}_{t}\oplus \text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{w}_{t}})$
; -
(v)
 $\mathfrak{w}_{s}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}}\subset \mathfrak{u}_{t}$
for any
$\mathfrak{w}_{s}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}}\subset \mathfrak{u}_{t}$
for any
 $s<t$
.
$s<t$
.
Proof. (i) We have
 $\unicode[STIX]{x1D714}([Z,a],b)+\unicode[STIX]{x1D714}(a,[Z,b])=\unicode[STIX]{x1D711}([[Z,a],b])+\unicode[STIX]{x1D711}([a,[Z,b]]\rangle =(\text{ad}^{\ast }(Z)(\unicode[STIX]{x1D711}))([a,b])=0$
.
$\unicode[STIX]{x1D714}([Z,a],b)+\unicode[STIX]{x1D714}(a,[Z,b])=\unicode[STIX]{x1D711}([[Z,a],b])+\unicode[STIX]{x1D711}([a,[Z,b]]\rangle =(\text{ad}^{\ast }(Z)(\unicode[STIX]{x1D711}))([a,b])=0$
.
(ii) We have
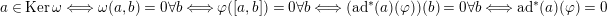 $a\in \text{Ker}\,\unicode[STIX]{x1D714}\;\Longleftrightarrow \;\unicode[STIX]{x1D714}(a,b)=0\forall b\;\Longleftrightarrow \;\unicode[STIX]{x1D711}([a,b])=0\forall b\;\Longleftrightarrow \;(\text{ad}^{\ast }(a)(\unicode[STIX]{x1D711}))(b)=0\forall b\;\Longleftrightarrow \;\text{ad}^{\ast }(a)(\unicode[STIX]{x1D711})=0$
. Thus
$a\in \text{Ker}\,\unicode[STIX]{x1D714}\;\Longleftrightarrow \;\unicode[STIX]{x1D714}(a,b)=0\forall b\;\Longleftrightarrow \;\unicode[STIX]{x1D711}([a,b])=0\forall b\;\Longleftrightarrow \;(\text{ad}^{\ast }(a)(\unicode[STIX]{x1D711}))(b)=0\forall b\;\Longleftrightarrow \;\text{ad}^{\ast }(a)(\unicode[STIX]{x1D711})=0$
. Thus
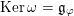 $\text{Ker}\,\unicode[STIX]{x1D714}=\mathfrak{g}_{\unicode[STIX]{x1D711}}$
. Since
$\text{Ker}\,\unicode[STIX]{x1D714}=\mathfrak{g}_{\unicode[STIX]{x1D711}}$
. Since
![]() $\unicode[STIX]{x1D711}$
is given by pairing with
$\unicode[STIX]{x1D711}$
is given by pairing with
![]() $f$
, its stabilizer
$f$
, its stabilizer
![]() $\mathfrak{g}_{\unicode[STIX]{x1D711}}$
coincides with the space
$\mathfrak{g}_{\unicode[STIX]{x1D711}}$
coincides with the space
![]() $\mathfrak{g}^{f}$
that is spanned by the lowest-weight vectors.
$\mathfrak{g}^{f}$
that is spanned by the lowest-weight vectors.
(iii) We have
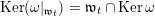 $\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{w}_{t}})=\mathfrak{w}_{t}\cap \text{Ker}\,\unicode[STIX]{x1D714}$
since
$\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{w}_{t}})=\mathfrak{w}_{t}\cap \text{Ker}\,\unicode[STIX]{x1D714}$
since
 $\unicode[STIX]{x1D714}(\mathfrak{w}_{t},\mathfrak{g}_{s}^{S_{t}})=0$
for any
$\unicode[STIX]{x1D714}(\mathfrak{w}_{t},\mathfrak{g}_{s}^{S_{t}})=0$
for any
![]() $s\neq -1$
. Now
$s\neq -1$
. Now
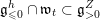 $\mathfrak{g}_{{\leqslant}0}^{h}\cap \mathfrak{w}_{t}\subset \mathfrak{g}_{{>}0}^{Z}$
.
$\mathfrak{g}_{{\leqslant}0}^{h}\cap \mathfrak{w}_{t}\subset \mathfrak{g}_{{>}0}^{Z}$
.
(iv) This holds since
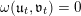 $\unicode[STIX]{x1D714}(\mathfrak{u}_{t},\mathfrak{v}_{t})=0$
.
$\unicode[STIX]{x1D714}(\mathfrak{u}_{t},\mathfrak{v}_{t})=0$
.
(v) Let
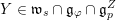 $Y\in \mathfrak{w}_{s}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{g}_{p}^{Z}$
. If
$Y\in \mathfrak{w}_{s}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{g}_{p}^{Z}$
. If
![]() $p\geqslant 0$
, then
$p\geqslant 0$
, then
![]() $Y\in \mathfrak{u}_{t}$
. If
$Y\in \mathfrak{u}_{t}$
. If
![]() $p<0$
, then
$p<0$
, then
 $Y\in \mathfrak{g}_{{\geqslant}1}^{S}$
. By the conditions of the theorem we have
$Y\in \mathfrak{g}_{{\geqslant}1}^{S}$
. By the conditions of the theorem we have
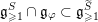 $\mathfrak{g}_{{\geqslant}1}^{S}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}}\subset \mathfrak{g}_{{\geqslant}1}^{\widetilde{S}}$
, thus
$\mathfrak{g}_{{\geqslant}1}^{S}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}}\subset \mathfrak{g}_{{\geqslant}1}^{\widetilde{S}}$
, thus
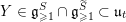 $Y\in \mathfrak{g}_{{\geqslant}1}^{S}\cap \mathfrak{g}_{{\geqslant}1}^{\widetilde{S}}\subset \mathfrak{u}_{t}$
.◻
$Y\in \mathfrak{g}_{{\geqslant}1}^{S}\cap \mathfrak{g}_{{\geqslant}1}^{\widetilde{S}}\subset \mathfrak{u}_{t}$
.◻
Choose a Lagrangian
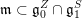 $\mathfrak{m}\subset \mathfrak{g}_{0}^{Z}\cap \mathfrak{g}_{1}^{S}$
and let
$\mathfrak{m}\subset \mathfrak{g}_{0}^{Z}\cap \mathfrak{g}_{1}^{S}$
and let
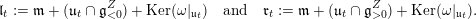 $$\begin{eqnarray}\mathfrak{l}_{t}:=\mathfrak{m}+(\mathfrak{u}_{t}\cap \mathfrak{g}_{{<}0}^{Z})+\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{ u}_{t}})\quad \text{and}\quad \mathfrak{r}_{t}:=\mathfrak{m}+(\mathfrak{u}_{t}\cap \mathfrak{g}_{{>}0}^{Z})+\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{ u}_{t}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{l}_{t}:=\mathfrak{m}+(\mathfrak{u}_{t}\cap \mathfrak{g}_{{<}0}^{Z})+\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{ u}_{t}})\quad \text{and}\quad \mathfrak{r}_{t}:=\mathfrak{m}+(\mathfrak{u}_{t}\cap \mathfrak{g}_{{>}0}^{Z})+\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{ u}_{t}}).\end{eqnarray}$$
Lemma 3.2.7.
![]() $\text{(i)}$
The spaces
$\text{(i)}$
The spaces
![]() $\mathfrak{l}_{t}$
and
$\mathfrak{l}_{t}$
and
![]() $\mathfrak{r}_{t}$
are ideals in
$\mathfrak{r}_{t}$
are ideals in
![]() $\mathfrak{u}_{t}$
and
$\mathfrak{u}_{t}$
and
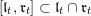 $[\mathfrak{l}_{t},\mathfrak{r}_{t}]\subset \mathfrak{l}_{t}\cap \mathfrak{r}_{t}$
.
$[\mathfrak{l}_{t},\mathfrak{r}_{t}]\subset \mathfrak{l}_{t}\cap \mathfrak{r}_{t}$
.
-
(ii) For any
 $t\geqslant 0$
,
$t\geqslant 0$
,
 $\mathfrak{l}_{t}$
and
$\mathfrak{l}_{t}$
and
 $\mathfrak{r}_{t}$
are maximal isotropic subspaces of
$\mathfrak{r}_{t}$
are maximal isotropic subspaces of
 $\mathfrak{u}_{t}$
.
$\mathfrak{u}_{t}$
.
-
(iii) Suppose that
 $0\leqslant s<t$
, and all elements of the open interval
$0\leqslant s<t$
, and all elements of the open interval
 $(s,t)$
are regular. Then
$(s,t)$
are regular. Then
 $\mathfrak{r}_{s}\subset \mathfrak{l}_{t}$
.
$\mathfrak{r}_{s}\subset \mathfrak{l}_{t}$
.
Proof. (i) This follows from the inclusion
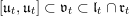 $[\mathfrak{u}_{t},\mathfrak{u}_{t}]\subset \mathfrak{v}_{t}\subset \mathfrak{l}_{t}\cap \mathfrak{r}_{t}$
.
$[\mathfrak{u}_{t},\mathfrak{u}_{t}]\subset \mathfrak{v}_{t}\subset \mathfrak{l}_{t}\cap \mathfrak{r}_{t}$
.
(ii) Since
![]() $\unicode[STIX]{x1D714}$
is
$\unicode[STIX]{x1D714}$
is
![]() $\text{ad}(Z)$
-invariant, we see that
$\text{ad}(Z)$
-invariant, we see that
![]() $\mathfrak{l}_{t}$
and
$\mathfrak{l}_{t}$
and
![]() $\mathfrak{r}_{t}$
are isotropic. To show that
$\mathfrak{r}_{t}$
are isotropic. To show that
![]() $\mathfrak{l}_{t}$
is maximal isotropic, let
$\mathfrak{l}_{t}$
is maximal isotropic, let
 $Y\in \mathfrak{g}_{s}^{Z}\cap \mathfrak{u}_{t}$
. Let
$Y\in \mathfrak{g}_{s}^{Z}\cap \mathfrak{u}_{t}$
. Let
![]() $R$
denote the radical of
$R$
denote the radical of
![]() $\unicode[STIX]{x1D714}|_{\mathfrak{u}_{t}}$
. If
$\unicode[STIX]{x1D714}|_{\mathfrak{u}_{t}}$
. If
![]() $Y\in R$
, then
$Y\in R$
, then
![]() $Y\in \mathfrak{l}_{t}$
. If
$Y\in \mathfrak{l}_{t}$
. If
![]() $s\leqslant 0$
, then
$s\leqslant 0$
, then
![]() $Y\in \mathfrak{l}_{t}$
. If
$Y\in \mathfrak{l}_{t}$
. If
![]() $s>0$
and
$s>0$
and
![]() $Y\notin R$
, then there exists
$Y\notin R$
, then there exists
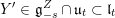 $Y^{\prime }\in \mathfrak{g}_{-s}^{Z}\cap \mathfrak{u}_{t}\subset \mathfrak{l}_{t}$
such that
$Y^{\prime }\in \mathfrak{g}_{-s}^{Z}\cap \mathfrak{u}_{t}\subset \mathfrak{l}_{t}$
such that
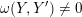 $\unicode[STIX]{x1D714}(Y,Y^{\prime })\neq 0$
. Thus, if we enlarge
$\unicode[STIX]{x1D714}(Y,Y^{\prime })\neq 0$
. Thus, if we enlarge
![]() $\mathfrak{l}_{t}$
it will stop being isotropic. Now, note that
$\mathfrak{l}_{t}$
it will stop being isotropic. Now, note that
![]() $\unicode[STIX]{x1D714}$
defines a symplectic structure on
$\unicode[STIX]{x1D714}$
defines a symplectic structure on
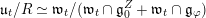 $\mathfrak{u}_{t}/R\simeq \mathfrak{w}_{t}/(\mathfrak{w}_{t}\cap \mathfrak{g}_{0}^{Z}+\mathfrak{w}_{t}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}})$
, and the image of
$\mathfrak{u}_{t}/R\simeq \mathfrak{w}_{t}/(\mathfrak{w}_{t}\cap \mathfrak{g}_{0}^{Z}+\mathfrak{w}_{t}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}})$
, and the image of
![]() $\mathfrak{l}_{t}$
in this space is Lagrangian. The image of
$\mathfrak{l}_{t}$
in this space is Lagrangian. The image of
![]() $\mathfrak{r}_{t}$
is a complementary isotropic subspace, thus also a Lagrangian, and thus
$\mathfrak{r}_{t}$
is a complementary isotropic subspace, thus also a Lagrangian, and thus
![]() $\mathfrak{r}_{t}$
itself is maximal isotropic in
$\mathfrak{r}_{t}$
itself is maximal isotropic in
![]() $\mathfrak{u}_{t}$
.
$\mathfrak{u}_{t}$
.
(iii) Note that
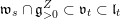 $\mathfrak{w}_{s}\cap \mathfrak{g}_{{>}0}^{Z}\subset \mathfrak{v}_{t}\subset \mathfrak{l}_{t}$
. Let us show that
$\mathfrak{w}_{s}\cap \mathfrak{g}_{{>}0}^{Z}\subset \mathfrak{v}_{t}\subset \mathfrak{l}_{t}$
. Let us show that
![]() $\mathfrak{v}_{s}\subset \mathfrak{l}_{t}$
. Note that
$\mathfrak{v}_{s}\subset \mathfrak{l}_{t}$
. Note that
![]() $\mathfrak{v}_{s}\subset \mathfrak{u}_{t}$
, since all elements in
$\mathfrak{v}_{s}\subset \mathfrak{u}_{t}$
, since all elements in
![]() $(s,t)$
are regular. Let
$(s,t)$
are regular. Let
![]() $Y\in \mathfrak{v}_{s}$
be a joint eigenvector for
$Y\in \mathfrak{v}_{s}$
be a joint eigenvector for
![]() $\text{ad}(S)$
and
$\text{ad}(S)$
and
![]() $\text{ad}(Z)$
. If
$\text{ad}(Z)$
. If
![]() $Y\notin \mathfrak{v}_{t}$
, then
$Y\notin \mathfrak{v}_{t}$
, then
![]() $Y\in \mathfrak{w}_{t}$
and its
$Y\in \mathfrak{w}_{t}$
and its
![]() $Z$
-eigenvalue is negative. Thus,
$Z$
-eigenvalue is negative. Thus,
![]() $Y\in \mathfrak{l}_{t}$
. Now by Lemma 3.2.6(v) we get
$Y\in \mathfrak{l}_{t}$
. Now by Lemma 3.2.6(v) we get
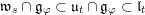 $\mathfrak{w}_{s}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}}\subset \mathfrak{u}_{t}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}}\subset \mathfrak{l}_{t}$
, and from Lemma 3.2.6(ii)–(iv) this implies
$\mathfrak{w}_{s}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}}\subset \mathfrak{u}_{t}\cap \mathfrak{g}_{\unicode[STIX]{x1D711}}\subset \mathfrak{l}_{t}$
, and from Lemma 3.2.6(ii)–(iv) this implies
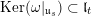 $\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{u}_{s}})\subset \mathfrak{l}_{t}$
. Altogether we get
$\text{Ker}(\unicode[STIX]{x1D714}|_{\mathfrak{u}_{s}})\subset \mathfrak{l}_{t}$
. Altogether we get
![]() $\mathfrak{r}_{s}\subset \mathfrak{l}_{t}$
.◻
$\mathfrak{r}_{s}\subset \mathfrak{l}_{t}$
.◻
Define
 $$\begin{eqnarray}\mathfrak{l}_{t}^{\prime }:=\mathfrak{l}_{t}\cap \text{Ker}(\unicode[STIX]{x1D711}^{\prime })\quad \text{and}\quad \mathfrak{r}_{t}^{\prime }:=\mathfrak{r}_{t}\cap \text{Ker}(\unicode[STIX]{x1D711}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{l}_{t}^{\prime }:=\mathfrak{l}_{t}\cap \text{Ker}(\unicode[STIX]{x1D711}^{\prime })\quad \text{and}\quad \mathfrak{r}_{t}^{\prime }:=\mathfrak{r}_{t}\cap \text{Ker}(\unicode[STIX]{x1D711}^{\prime }).\end{eqnarray}$$
Lemma 3.2.8.
![]() $\text{(i)}$
For any
$\text{(i)}$
For any
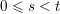 $0\leqslant s<t$
such that all of the numbers in the open interval
$0\leqslant s<t$
such that all of the numbers in the open interval
![]() $(s,t)$
are regular, we have
$(s,t)$
are regular, we have
![]() $\mathfrak{r}_{s}^{\prime }\subset \mathfrak{l}_{t}^{\prime }$
.
$\mathfrak{r}_{s}^{\prime }\subset \mathfrak{l}_{t}^{\prime }$
.
-
(ii) For
 $0\leqslant t<1$
, both
$0\leqslant t<1$
, both
 $\mathfrak{l}_{t}^{\prime }$
and
$\mathfrak{l}_{t}^{\prime }$
and
 $\mathfrak{r}_{t}^{\prime }$
are subalgebras of
$\mathfrak{r}_{t}^{\prime }$
are subalgebras of
 $\mathfrak{u}_{t}$
,
$\mathfrak{u}_{t}$
,
 $[\mathfrak{l}_{t}^{\prime },\mathfrak{r}_{t}^{\prime }]\subset \mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
and for
$[\mathfrak{l}_{t}^{\prime },\mathfrak{r}_{t}^{\prime }]\subset \mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
and for
 $0\leqslant t<(i+1)/(i+2)$
we have
$0\leqslant t<(i+1)/(i+2)$
we have
 $\mathfrak{l}_{t}^{\prime }=\mathfrak{l}_{t}$
and
$\mathfrak{l}_{t}^{\prime }=\mathfrak{l}_{t}$
and
 $\mathfrak{r}_{t}^{\prime }=\mathfrak{r}_{t}$
.
$\mathfrak{r}_{t}^{\prime }=\mathfrak{r}_{t}$
.
-
(iii) The radical
 $\mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
is of
$\mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
is of
 $\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}^{\prime }+\mathfrak{r}_{t}^{\prime }}$
.
$\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}^{\prime }+\mathfrak{r}_{t}^{\prime }}$
.
Proof. Part (i) follows immediately from Lemma 3.2.7(iii).
For part (ii) note that
![]() $i\geqslant 0$
,
$i\geqslant 0$
,
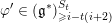 $\unicode[STIX]{x1D711}^{\prime }\in (\mathfrak{g}^{\ast })_{{\geqslant}i-t(i+2)}^{S_{t}}$
and thus
$\unicode[STIX]{x1D711}^{\prime }\in (\mathfrak{g}^{\ast })_{{\geqslant}i-t(i+2)}^{S_{t}}$
and thus
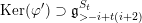 $\text{Ker}(\unicode[STIX]{x1D711}^{\prime })\supset \mathfrak{g}_{{>}-i+t(i+2)}^{S_{t}}$
. Thus, for
$\text{Ker}(\unicode[STIX]{x1D711}^{\prime })\supset \mathfrak{g}_{{>}-i+t(i+2)}^{S_{t}}$
. Thus, for
![]() $t<1$
we have
$t<1$
we have
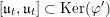 $[\mathfrak{u}_{t},\mathfrak{u}_{t}]\subset \text{Ker}(\unicode[STIX]{x1D711}^{\prime })$
and for
$[\mathfrak{u}_{t},\mathfrak{u}_{t}]\subset \text{Ker}(\unicode[STIX]{x1D711}^{\prime })$
and for
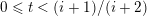 $0\leqslant t<(i+1)/(i+2)$
we have
$0\leqslant t<(i+1)/(i+2)$
we have
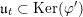 $\mathfrak{u}_{t}\subset \text{Ker}(\unicode[STIX]{x1D711}^{\prime })$
. Since
$\mathfrak{u}_{t}\subset \text{Ker}(\unicode[STIX]{x1D711}^{\prime })$
. Since
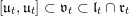 $[\mathfrak{u}_{t},\mathfrak{u}_{t}]\subset \mathfrak{v}_{t}\subset \mathfrak{l}_{t}\cap \mathfrak{r}_{t}$
we obtain (ii).
$[\mathfrak{u}_{t},\mathfrak{u}_{t}]\subset \mathfrak{v}_{t}\subset \mathfrak{l}_{t}\cap \mathfrak{r}_{t}$
we obtain (ii).
For part (iii) we can assume that
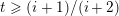 $t\geqslant (i+1)/(i+2)$
and
$t\geqslant (i+1)/(i+2)$
and
![]() $\unicode[STIX]{x1D711}^{\prime }\neq 0$
. Then, by Lemma 3.2.4, there exists
$\unicode[STIX]{x1D711}^{\prime }\neq 0$
. Then, by Lemma 3.2.4, there exists
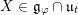 $X\in \mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{u}_{t}$
with
$X\in \mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{u}_{t}$
with
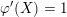 $\unicode[STIX]{x1D711}^{\prime }(X)=1$
. Thus, the image of
$\unicode[STIX]{x1D711}^{\prime }(X)=1$
. Thus, the image of
![]() $\mathfrak{l}_{t}^{\prime }$
in
$\mathfrak{l}_{t}^{\prime }$
in
 $\mathfrak{u}_{t}/(\mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{u}_{t})$
coincides with the image of
$\mathfrak{u}_{t}/(\mathfrak{g}_{\unicode[STIX]{x1D711}}\cap \mathfrak{u}_{t})$
coincides with the image of
![]() $\mathfrak{l}_{t}$
, and the image of
$\mathfrak{l}_{t}$
, and the image of
![]() $\mathfrak{r}_{t}^{\prime }$
coincides with the image of
$\mathfrak{r}_{t}^{\prime }$
coincides with the image of
![]() $\mathfrak{r}_{t}$
. Since those images are Lagrangian,
$\mathfrak{r}_{t}$
. Since those images are Lagrangian,
![]() $\mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
is the radical of
$\mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
is the radical of
![]() $\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}^{\prime }+\mathfrak{r}_{t}^{\prime }}$
.◻
$\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}^{\prime }+\mathfrak{r}_{t}^{\prime }}$
.◻
Lemmas 3.2.8 and 3.2.1 imply that
 $$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{0})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{0}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}},\quad \text{ind}_{\text{Exp}(\mathfrak{l}_{t}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{t}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{0})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{0}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}},\quad \text{ind}_{\text{Exp}(\mathfrak{l}_{t}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{t}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\end{eqnarray}$$
and for
![]() $s<t$
such that all the numbers in
$s<t$
such that all the numbers in
![]() $(s,t)$
are regular we have
$(s,t)$
are regular we have
 $$\begin{eqnarray}\text{ind}_{\text{Exp}(\mathfrak{r}_{s}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\,{\twoheadrightarrow}\,\text{ind}_{\text{Exp}(\mathfrak{l}_{t}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{ind}_{\text{Exp}(\mathfrak{r}_{s}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\,{\twoheadrightarrow}\,\text{ind}_{\text{Exp}(\mathfrak{l}_{t}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}.\end{eqnarray}$$
We are now ready to prove Theorem 3.0.1.
Proof of Theorem 3.0.1.
Let
 $0<t_{1}<\cdots <t_{n}$
be the critical numbers. Note that
$0<t_{1}<\cdots <t_{n}$
be the critical numbers. Note that
![]() $\mathfrak{r}_{t_{n}}^{\prime }$
is an isotropic subalgebra of
$\mathfrak{r}_{t_{n}}^{\prime }$
is an isotropic subalgebra of
![]() $\mathfrak{u}_{1}$
, and that it is also isotropic with respect to the form
$\mathfrak{u}_{1}$
, and that it is also isotropic with respect to the form
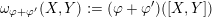 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }}(X,Y):=(\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime })([X,Y])$
. Let
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }}(X,Y):=(\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime })([X,Y])$
. Let
![]() $\mathfrak{q}$
be a maximal isotropic subspace of
$\mathfrak{q}$
be a maximal isotropic subspace of
![]() $\mathfrak{u}_{1}$
with respect to this form. It includes
$\mathfrak{u}_{1}$
with respect to this form. It includes
![]() $\mathfrak{v}_{1}$
and thus is necessary a subalgebra. Note that
$\mathfrak{v}_{1}$
and thus is necessary a subalgebra. Note that
 $$\begin{eqnarray}\text{ind}_{\text{Exp}(\mathfrak{r}_{t_{n}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}=\text{ind}_{\text{Exp}(\mathfrak{r}_{t_{n}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }}\,{\twoheadrightarrow}\,\text{ind}_{\text{Exp}(\mathfrak{q})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }}\simeq {\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}^{\prime }}\simeq {\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{ind}_{\text{Exp}(\mathfrak{r}_{t_{n}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}=\text{ind}_{\text{Exp}(\mathfrak{r}_{t_{n}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }}\,{\twoheadrightarrow}\,\text{ind}_{\text{Exp}(\mathfrak{q})}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}+\unicode[STIX]{x1D711}^{\prime }}\simeq {\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}^{\prime }}\simeq {\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}.\end{eqnarray}$$
Thus,
 $$\begin{eqnarray}\displaystyle {\mathcal{W}}_{S,\unicode[STIX]{x1D711}} & \simeq & \displaystyle \text{ind}_{\text{Exp}(\mathfrak{r}_{0}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\,{\twoheadrightarrow}\,\text{ind}_{\text{Exp}(\mathfrak{l}_{t_{1}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{t_{1}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}{\twoheadrightarrow}\nonumber\\ \displaystyle & & \displaystyle \cdots \,{\twoheadrightarrow}\,\text{ind}_{\text{Exp}(\mathfrak{l}_{t_{n}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{t_{n}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\,{\twoheadrightarrow}\,{\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{W}}_{S,\unicode[STIX]{x1D711}} & \simeq & \displaystyle \text{ind}_{\text{Exp}(\mathfrak{r}_{0}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\,{\twoheadrightarrow}\,\text{ind}_{\text{Exp}(\mathfrak{l}_{t_{1}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{t_{1}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}{\twoheadrightarrow}\nonumber\\ \displaystyle & & \displaystyle \cdots \,{\twoheadrightarrow}\,\text{ind}_{\text{Exp}(\mathfrak{l}_{t_{n}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{t_{n}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\,{\twoheadrightarrow}\,{\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}.\end{eqnarray}$$
◻
Remark 3.2.9. Observe that, in the above proof, the map
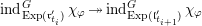 $\text{ind}_{\text{Exp}(\mathfrak{r}_{t_{i}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\,{\twoheadrightarrow}\,\text{ind}_{\text{Exp}(\mathfrak{l}_{t_{i+1}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
is simply given by integration over
$\text{ind}_{\text{Exp}(\mathfrak{r}_{t_{i}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}\,{\twoheadrightarrow}\,\text{ind}_{\text{Exp}(\mathfrak{l}_{t_{i+1}}^{\prime })}^{G}\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
is simply given by integration over
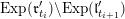 $\text{Exp}(\mathfrak{r}_{t_{i}}^{\prime })\backslash \text{Exp}(\mathfrak{l}_{t_{i+1}}^{\prime })$
. From this, and the observation given in Remark 3.2.2, we see that the
$\text{Exp}(\mathfrak{r}_{t_{i}}^{\prime })\backslash \text{Exp}(\mathfrak{l}_{t_{i+1}}^{\prime })$
. From this, and the observation given in Remark 3.2.2, we see that the
![]() $G$
-equivariant epimorphism promised in Theorem 3.0.1 is given by a series of integral transforms followed, if necessary, by conjugation by an element of
$G$
-equivariant epimorphism promised in Theorem 3.0.1 is given by a series of integral transforms followed, if necessary, by conjugation by an element of
![]() $G$
.
$G$
.
Remark 3.2.10. Let
![]() $M$
denote the joint centralizer of
$M$
denote the joint centralizer of
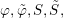 $\unicode[STIX]{x1D711},\tilde{\unicode[STIX]{x1D711}},S,\tilde{S},$
and
$\unicode[STIX]{x1D711},\tilde{\unicode[STIX]{x1D711}},S,\tilde{S},$
and
![]() $h$
. Then a central extension
$h$
. Then a central extension
![]() $\tilde{M}$
of
$\tilde{M}$
of
![]() $M$
acts naturally on the oscillator representations
$M$
acts naturally on the oscillator representations
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
and
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D711}}$
and
![]() $\unicode[STIX]{x1D70E}_{\tilde{\unicode[STIX]{x1D711}}}$
, and thus also on the degenerate Whittaker models
$\unicode[STIX]{x1D70E}_{\tilde{\unicode[STIX]{x1D711}}}$
, and thus also on the degenerate Whittaker models
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
and
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
and
![]() ${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}.$
It is easy to see that the constructed epimorphism
${\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}.$
It is easy to see that the constructed epimorphism
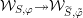 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}{\twoheadrightarrow}{\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}$
intertwines these actions.
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}{\twoheadrightarrow}{\mathcal{W}}_{\widetilde{S},\tilde{\unicode[STIX]{x1D711}}}$
intertwines these actions.
Let us now present two examples for the elements and subalgebras defined in the course of the proof. Let
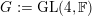 $G:=\text{GL}(4,\mathbb{F})$
and define
$G:=\text{GL}(4,\mathbb{F})$
and define
![]() $\unicode[STIX]{x1D711}$
by
$\unicode[STIX]{x1D711}$
by
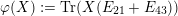 $\unicode[STIX]{x1D711}(X):=\text{Tr}(X(E_{21}+E_{43}))$
, where
$\unicode[STIX]{x1D711}(X):=\text{Tr}(X(E_{21}+E_{43}))$
, where
![]() $E_{21}$
and
$E_{21}$
and
![]() $E_{43}$
are elementary matrices. Let
$E_{43}$
are elementary matrices. Let
![]() $h$
be the diagonal matrix
$h$
be the diagonal matrix
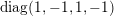 $\text{diag}(1,-1,1,-1)$
and
$\text{diag}(1,-1,1,-1)$
and
![]() $S:=h$
.
$S:=h$
.
Example 3.2.11. Let
![]() $\tilde{\unicode[STIX]{x1D711}}:=\unicode[STIX]{x1D711}$
,
$\tilde{\unicode[STIX]{x1D711}}:=\unicode[STIX]{x1D711}$
,
 $K:=\text{diag}(3,1,-1,-3)$
,
$K:=\text{diag}(3,1,-1,-3)$
,
![]() $z:=0$
. Then
$z:=0$
. Then
 $Z=\text{diag}(2,2,-2,-2),S_{t}=\text{diag}(1+2t,-1+2t,1-2t,-1-2t)$
and the weights of
$Z=\text{diag}(2,2,-2,-2),S_{t}=\text{diag}(1+2t,-1+2t,1-2t,-1-2t)$
and the weights of
![]() $S_{t}$
are as follows:
$S_{t}$
are as follows:
 $$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}0 & 2 & 4t & 4t+2\\ -2 & 0 & 4t-2 & 4t\\ -4t & -4t+2 & 0 & 2\\ -4t-2 & -4t & -2 & 0\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}0 & 2 & 4t & 4t+2\\ -2 & 0 & 4t-2 & 4t\\ -4t & -4t+2 & 0 & 2\\ -4t-2 & -4t & -2 & 0\end{array}\right).\end{eqnarray}$$
The critical numbers are
![]() $1/4$
and
$1/4$
and
![]() $3/4$
. For
$3/4$
. For
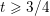 $t\geqslant 3/4$
we get the principal degenerate Whittaker model. We have
$t\geqslant 3/4$
we get the principal degenerate Whittaker model. We have
 $\mathfrak{r}_{t}^{\prime }=\mathfrak{r}_{t},\mathfrak{l}_{t}^{\prime }=\mathfrak{l}_{t}$
for all
$\mathfrak{r}_{t}^{\prime }=\mathfrak{r}_{t},\mathfrak{l}_{t}^{\prime }=\mathfrak{l}_{t}$
for all
![]() $t$
. The above system of inclusions of
$t$
. The above system of inclusions of
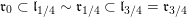 $\mathfrak{r}_{0}\subset \mathfrak{l}_{1/4}\sim \mathfrak{r}_{1/4}\subset \mathfrak{l}_{3/4}=\mathfrak{r}_{3/4}$
is
$\mathfrak{r}_{0}\subset \mathfrak{l}_{1/4}\sim \mathfrak{r}_{1/4}\subset \mathfrak{l}_{3/4}=\mathfrak{r}_{3/4}$
is
 $$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}0 & - & 0 & -\\ 0 & 0 & 0 & 0\\ 0 & - & 0 & -\\ 0 & 0 & 0 & 0\end{array}\right)\subset \left(\begin{array}{@{}cccc@{}}0 & - & a & -\\ 0 & 0 & 0 & a\\ 0 & \ast & 0 & -\\ 0 & 0 & 0 & 0\end{array}\right)\sim \left(\begin{array}{@{}cccc@{}}0 & - & \ast & -\\ 0 & 0 & 0 & \ast \\ 0 & 0 & 0 & -\\ 0 & 0 & 0 & 0\end{array}\right)\subset \left(\begin{array}{@{}cccc@{}}0 & - & - & -\\ 0 & 0 & \ast & -\\ 0 & 0 & 0 & -\\ 0 & 0 & 0 & 0\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}0 & - & 0 & -\\ 0 & 0 & 0 & 0\\ 0 & - & 0 & -\\ 0 & 0 & 0 & 0\end{array}\right)\subset \left(\begin{array}{@{}cccc@{}}0 & - & a & -\\ 0 & 0 & 0 & a\\ 0 & \ast & 0 & -\\ 0 & 0 & 0 & 0\end{array}\right)\sim \left(\begin{array}{@{}cccc@{}}0 & - & \ast & -\\ 0 & 0 & 0 & \ast \\ 0 & 0 & 0 & -\\ 0 & 0 & 0 & 0\end{array}\right)\subset \left(\begin{array}{@{}cccc@{}}0 & - & - & -\\ 0 & 0 & \ast & -\\ 0 & 0 & 0 & -\\ 0 & 0 & 0 & 0\end{array}\right).\end{eqnarray}$$
Here, both
![]() $\ast$
and
$\ast$
and
![]() $-$
denote arbitrary elements:
$-$
denote arbitrary elements:
![]() $-$
denotes the entries in
$-$
denotes the entries in
![]() $\mathfrak{v}_{t}$
and
$\mathfrak{v}_{t}$
and
![]() $\ast$
those in
$\ast$
those in
![]() $\mathfrak{w}_{t}$
. The letter
$\mathfrak{w}_{t}$
. The letter
![]() $a$
denotes an arbitrary element, but the two appearances of
$a$
denotes an arbitrary element, but the two appearances of
![]() $a$
denote the same numbers. The passage from
$a$
denote the same numbers. The passage from
![]() $\mathfrak{l}_{1/4}$
to
$\mathfrak{l}_{1/4}$
to
![]() $\mathfrak{r}_{1/4}$
is denoted by
$\mathfrak{r}_{1/4}$
is denoted by
![]() ${\sim}$
. At
${\sim}$
. At
![]() $3/4$
we have
$3/4$
we have
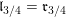 $\mathfrak{l}_{3/4}=\mathfrak{r}_{3/4}$
.
$\mathfrak{l}_{3/4}=\mathfrak{r}_{3/4}$
.
Let us now give an example in which
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $\tilde{\unicode[STIX]{x1D711}}$
are not equal and not conjugate.
$\tilde{\unicode[STIX]{x1D711}}$
are not equal and not conjugate.
Example 3.2.12. Identify
![]() $\mathfrak{g}\simeq \mathfrak{g}^{\ast }$
using the trace form and let
$\mathfrak{g}\simeq \mathfrak{g}^{\ast }$
using the trace form and let
 $$\begin{eqnarray}\tilde{\unicode[STIX]{x1D711}}=\left(\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ 1 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\end{array}\right),\quad e=\left(\begin{array}{@{}cccc@{}}0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\end{array}\right),\quad \unicode[STIX]{x1D711}^{\prime }=\left(\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D711}}=\left(\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ 1 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\end{array}\right),\quad e=\left(\begin{array}{@{}cccc@{}}0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\end{array}\right),\quad \unicode[STIX]{x1D711}^{\prime }=\left(\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\end{array}\right).\end{eqnarray}$$
Let
 $\widetilde{S}:=\text{diag}(0,-2,2,0)$
,
$\widetilde{S}:=\text{diag}(0,-2,2,0)$
,
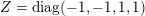 $Z=\text{diag}(-1,-1,1,1)$
. Note that
$Z=\text{diag}(-1,-1,1,1)$
. Note that
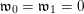 $\mathfrak{w}_{0}=\mathfrak{w}_{1}=0$
and the only critical value of
$\mathfrak{w}_{0}=\mathfrak{w}_{1}=0$
and the only critical value of
![]() $t$
is
$t$
is
![]() $1/2$
. The sequence of subalgebras from the proof of Theorem 3.0.1 is
$1/2$
. The sequence of subalgebras from the proof of Theorem 3.0.1 is
 $$\begin{eqnarray}\mathfrak{u}_{0}=l_{0}^{\prime }=\mathfrak{l}_{1/2}^{\prime }=\left(\begin{array}{@{}cccc@{}}0 & \ast & 0 & -\\ 0 & 0 & 0 & 0\\ 0 & \ast & 0 & \ast \\ 0 & 0 & 0 & 0\end{array}\right)\sim \mathfrak{r}_{1/2}^{\prime }=\left(\begin{array}{@{}cccc@{}}0 & \ast & 0 & 0\\ 0 & 0 & 0 & 0\\ a & \ast & 0 & \ast \\ 0 & -a & 0 & 0\end{array}\right)\subset \left(\begin{array}{@{}cccc@{}}0 & \ast & 0 & 0\\ 0 & 0 & 0 & 0\\ \ast & \ast & 0 & \ast \\ 0 & \ast & 0 & 0\end{array}\right)=\mathfrak{u}_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{u}_{0}=l_{0}^{\prime }=\mathfrak{l}_{1/2}^{\prime }=\left(\begin{array}{@{}cccc@{}}0 & \ast & 0 & -\\ 0 & 0 & 0 & 0\\ 0 & \ast & 0 & \ast \\ 0 & 0 & 0 & 0\end{array}\right)\sim \mathfrak{r}_{1/2}^{\prime }=\left(\begin{array}{@{}cccc@{}}0 & \ast & 0 & 0\\ 0 & 0 & 0 & 0\\ a & \ast & 0 & \ast \\ 0 & -a & 0 & 0\end{array}\right)\subset \left(\begin{array}{@{}cccc@{}}0 & \ast & 0 & 0\\ 0 & 0 & 0 & 0\\ \ast & \ast & 0 & \ast \\ 0 & \ast & 0 & 0\end{array}\right)=\mathfrak{u}_{1}.\end{eqnarray}$$
3.3 Principal degenerate Whittaker models and proof of theorem B
In the discussion below
![]() $\mathfrak{a}$
will denote a maximal split toral subalgebra of
$\mathfrak{a}$
will denote a maximal split toral subalgebra of
![]() $\mathfrak{g}$
, we will write
$\mathfrak{g}$
, we will write
![]() $\unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
for the corresponding (restricted) root system,
$\unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
for the corresponding (restricted) root system,
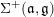 $\unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})$
for a choice of positive roots, and
$\unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})$
for a choice of positive roots, and
![]() $\unicode[STIX]{x1D6E5}(\mathfrak{a,g})$
for the corresponding system of simple roots.
$\unicode[STIX]{x1D6E5}(\mathfrak{a,g})$
for the corresponding system of simple roots.
Definition 3.3.1. We say that a rational semisimple
![]() $S\in \mathfrak{g}$
is principal if there exists an
$S\in \mathfrak{g}$
is principal if there exists an
![]() $\mathfrak{a}$
containing
$\mathfrak{a}$
containing
![]() $S$
, and a simple subsystem
$S$
, and a simple subsystem
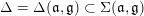 $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}(\mathfrak{a,g})\subset \unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
such that
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}(\mathfrak{a,g})\subset \unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
such that
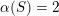 $\unicode[STIX]{x1D6FC}(S)=2$
for all
$\unicode[STIX]{x1D6FC}(S)=2$
for all
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. We say that a Whittaker pair
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. We say that a Whittaker pair
![]() $(S,\unicode[STIX]{x1D711})$
is principal if
$(S,\unicode[STIX]{x1D711})$
is principal if
![]() $S$
is principal. A principal degenerate Whittaker model is the degenerate Whittaker model corresponding to a principal Whittaker pair.
$S$
is principal. A principal degenerate Whittaker model is the degenerate Whittaker model corresponding to a principal Whittaker pair.
We fix a non-degenerate invariant bilinear form on
![]() $\mathfrak{g}$
, which allows us to identify nilpotent elements in
$\mathfrak{g}$
, which allows us to identify nilpotent elements in
![]() $\mathfrak{g}$
and
$\mathfrak{g}$
and
![]() $\mathfrak{g}^{\ast }$
. Thus, we may equally well apply the above terminology to ‘Whittaker pairs’
$\mathfrak{g}^{\ast }$
. Thus, we may equally well apply the above terminology to ‘Whittaker pairs’
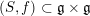 $(S,f)\subset \mathfrak{g}\times \mathfrak{g}$
, such that
$(S,f)\subset \mathfrak{g}\times \mathfrak{g}$
, such that
![]() $S$
is rational semisimple and
$S$
is rational semisimple and
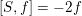 $[S,f]=-2f$
.
$[S,f]=-2f$
.
Note that a principal element
![]() $S$
uniquely determines both
$S$
uniquely determines both
![]() $\mathfrak{a}$
, and the simple system
$\mathfrak{a}$
, and the simple system
 $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}(\mathfrak{a,g})$
. Thus, there is a bijection between principal elements and simple systems which we denote by
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}(\mathfrak{a,g})$
. Thus, there is a bijection between principal elements and simple systems which we denote by
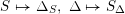 $S\mapsto \unicode[STIX]{x1D6E5}_{S},\text{ }\unicode[STIX]{x1D6E5}\mapsto S_{\unicode[STIX]{x1D6E5}}$
.
$S\mapsto \unicode[STIX]{x1D6E5}_{S},\text{ }\unicode[STIX]{x1D6E5}\mapsto S_{\unicode[STIX]{x1D6E5}}$
.
If
![]() $(S,f)$
is principal, then setting
$(S,f)$
is principal, then setting
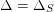 $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{S}$
, we can write
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{S}$
, we can write
![]() $f$
uniquely in the form
$f$
uniquely in the form
 $$\begin{eqnarray}f=\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}Y_{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
$$\begin{eqnarray}f=\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}Y_{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
for some
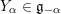 $Y_{\unicode[STIX]{x1D6FC}}\in \mathfrak{g}_{-\unicode[STIX]{x1D6FC}}$
. Conversely if
$Y_{\unicode[STIX]{x1D6FC}}\in \mathfrak{g}_{-\unicode[STIX]{x1D6FC}}$
. Conversely if
![]() $f$
is of the form (21) for some
$f$
is of the form (21) for some
![]() $\unicode[STIX]{x1D6E5}$
, then we will say that
$\unicode[STIX]{x1D6E5}$
, then we will say that
![]() $f$
is a PL nilpotent and
$f$
is a PL nilpotent and
![]() $\unicode[STIX]{x1D6E5}$
is compatible with
$\unicode[STIX]{x1D6E5}$
is compatible with
![]() $f$
. In this case
$f$
. In this case
![]() $\left(S_{\unicode[STIX]{x1D6E5}},f\right)$
is a principal Whittaker pair, and we define the
$\left(S_{\unicode[STIX]{x1D6E5}},f\right)$
is a principal Whittaker pair, and we define the
![]() $\unicode[STIX]{x1D6E5}$
-support of
$\unicode[STIX]{x1D6E5}$
-support of
![]() $f$
to be
$f$
to be
 $$\begin{eqnarray}\text{supp}_{\unicode[STIX]{x1D6E5}}(f)=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\mid Y_{\unicode[STIX]{x1D6FC}}\neq 0\}.\end{eqnarray}$$
$$\begin{eqnarray}\text{supp}_{\unicode[STIX]{x1D6E5}}(f)=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\mid Y_{\unicode[STIX]{x1D6FC}}\neq 0\}.\end{eqnarray}$$
If
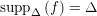 $\text{supp}_{\unicode[STIX]{x1D6E5}}\left(f\right)=\unicode[STIX]{x1D6E5}$
we say that
$\text{supp}_{\unicode[STIX]{x1D6E5}}\left(f\right)=\unicode[STIX]{x1D6E5}$
we say that
![]() $f$
is a principal nilpotent element. Note that this notion is weaker than the similar notion defined in [Reference BourbakiBou75, VIII.11.4]. However, if
$f$
is a principal nilpotent element. Note that this notion is weaker than the similar notion defined in [Reference BourbakiBou75, VIII.11.4]. However, if
![]() $G$
is quasi-split then both notions are equivalent to the notion of regular nilpotent element.
$G$
is quasi-split then both notions are equivalent to the notion of regular nilpotent element.
Note that
![]() $f$
is a PL nilpotent if and only if it is a principal nilpotent element for a Levi subgroup of
$f$
is a PL nilpotent if and only if it is a principal nilpotent element for a Levi subgroup of
![]() $G$
. For the general linear groups, every orbit includes such an element. For complex classical groups, all such orbits are described in [Reference Gourevitch and SahiGS15, § 6] in terms of the corresponding partitions. For complex exceptional groups, these are the orbits with non-parenthetical Bala–Carter labels.
$G$
. For the general linear groups, every orbit includes such an element. For complex classical groups, all such orbits are described in [Reference Gourevitch and SahiGS15, § 6] in terms of the corresponding partitions. For complex exceptional groups, these are the orbits with non-parenthetical Bala–Carter labels.
Lemma 3.3.2. Let
![]() $(S_{1},f)$
and
$(S_{1},f)$
and
![]() $(S_{2},f)$
be two Whittaker pairs with the same
$(S_{2},f)$
be two Whittaker pairs with the same
![]() $f$
, and let
$f$
, and let
![]() $h$
be neutral for
$h$
be neutral for
![]() $f$
. Then there exist
$f$
. Then there exist
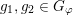 $g_{1},g_{2}\in G_{\unicode[STIX]{x1D711}}$
and
$g_{1},g_{2}\in G_{\unicode[STIX]{x1D711}}$
and
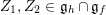 $Z_{1},Z_{2}\in \mathfrak{g}_{h}\cap \mathfrak{g}_{f}$
such that
$Z_{1},Z_{2}\in \mathfrak{g}_{h}\cap \mathfrak{g}_{f}$
such that
 $$\begin{eqnarray}g_{1}\cdot S_{1}=h+Z_{1},\quad g_{2}\cdot S_{2}=h+Z_{2},\quad [Z_{1},Z_{2}]=0.\end{eqnarray}$$
$$\begin{eqnarray}g_{1}\cdot S_{1}=h+Z_{1},\quad g_{2}\cdot S_{2}=h+Z_{2},\quad [Z_{1},Z_{2}]=0.\end{eqnarray}$$
Proof. By Lemma 3.0.2 we can find
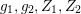 $g_{1},g_{2},Z_{1},Z_{2}$
satisfying all of the stated properties, except perhaps the commutativity
$g_{1},g_{2},Z_{1},Z_{2}$
satisfying all of the stated properties, except perhaps the commutativity
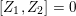 $[Z_{1},Z_{2}]=0$
. Since
$[Z_{1},Z_{2}]=0$
. Since
![]() $\mathfrak{g}_{h}\cap \mathfrak{g}_{f}$
is the centralizer of an
$\mathfrak{g}_{h}\cap \mathfrak{g}_{f}$
is the centralizer of an
![]() $\mathfrak{sl}_{2}$
-triple, it is reductive. Since
$\mathfrak{sl}_{2}$
-triple, it is reductive. Since
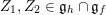 $Z_{1},Z_{2}\in \mathfrak{g}_{h}\cap \mathfrak{g}_{f}$
are rational semisimple, we can move them to a common Cartan subspace after further conjugation by elements of
$Z_{1},Z_{2}\in \mathfrak{g}_{h}\cap \mathfrak{g}_{f}$
are rational semisimple, we can move them to a common Cartan subspace after further conjugation by elements of
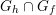 $G_{h}\cap G_{f}$
.◻
$G_{h}\cap G_{f}$
.◻
Proposition 3.3.3. Let
![]() $(S,f)$
be a Whittaker pair such that
$(S,f)$
be a Whittaker pair such that
![]() $f$
is a PL nilpotent. Then there exist a maximal split toral subalgebra
$f$
is a PL nilpotent. Then there exist a maximal split toral subalgebra
![]() $\mathfrak{a}$
, and a simple system
$\mathfrak{a}$
, and a simple system
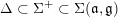 $\unicode[STIX]{x1D6E5}\subset \unicode[STIX]{x1D6F4}^{+}\subset \unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
such that:
$\unicode[STIX]{x1D6E5}\subset \unicode[STIX]{x1D6F4}^{+}\subset \unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
such that:
-
(a)
 $\unicode[STIX]{x1D6E5}$
is compatible with
$\unicode[STIX]{x1D6E5}$
is compatible with
 $f$
;
$f$
; -
(b)
 $\mathfrak{a}$
contains
$\mathfrak{a}$
contains
 $S$
;
$S$
; -
(c)
 $\mathfrak{a}$
contains a neutral element
$\mathfrak{a}$
contains a neutral element
 $h$
for
$h$
for
 $f$
;
$f$
; -
(d) if
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}$
satisfies
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}$
satisfies
 $\unicode[STIX]{x1D6FC}(h)\leqslant 0$
and
$\unicode[STIX]{x1D6FC}(h)\leqslant 0$
and
 $\unicode[STIX]{x1D6FC}(S)>0$
, then
$\unicode[STIX]{x1D6FC}(S)>0$
, then
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}^{+}$
.
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}^{+}$
.
Proof. Let us first choose any simple system
![]() $\unicode[STIX]{x1D6E5}(\mathfrak{b,g})$
compatible with
$\unicode[STIX]{x1D6E5}(\mathfrak{b,g})$
compatible with
![]() $f$
. By Lemma 3.3.2 there exists
$f$
. By Lemma 3.3.2 there exists
![]() $g$
in the centralizer
$g$
in the centralizer
![]() $G_{f}$
of
$G_{f}$
of
![]() $f$
such that
$f$
such that
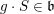 $g\cdot S\in \mathfrak{b}$
. Now the action of
$g\cdot S\in \mathfrak{b}$
. Now the action of
![]() $g^{-1}$
carries
$g^{-1}$
carries
![]() $\mathfrak{b}$
to a maximal toral subalgebra
$\mathfrak{b}$
to a maximal toral subalgebra
![]() $\mathfrak{a}$
and
$\mathfrak{a}$
and
![]() $\unicode[STIX]{x1D6E5}(\mathfrak{b,g})$
to a simple system
$\unicode[STIX]{x1D6E5}(\mathfrak{b,g})$
to a simple system
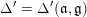 $\unicode[STIX]{x1D6E5}^{\prime }=\unicode[STIX]{x1D6E5}^{\prime }(\mathfrak{a,g})$
which satisfies parts (a) and (b). Next note that if
$\unicode[STIX]{x1D6E5}^{\prime }=\unicode[STIX]{x1D6E5}^{\prime }(\mathfrak{a,g})$
which satisfies parts (a) and (b). Next note that if
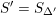 $S^{\prime }=S_{\unicode[STIX]{x1D6E5}^{\prime }}$
, then
$S^{\prime }=S_{\unicode[STIX]{x1D6E5}^{\prime }}$
, then
![]() $(S^{\prime },f)$
is a Whittaker pair, so by Lemma 3.0.2 there is a neutral element
$(S^{\prime },f)$
is a Whittaker pair, so by Lemma 3.0.2 there is a neutral element
![]() $h$
for
$h$
for
![]() $f$
that commutes with
$f$
that commutes with
![]() $S_{\unicode[STIX]{x1D6E5}^{\prime }}$
; but this forces
$S_{\unicode[STIX]{x1D6E5}^{\prime }}$
; but this forces
![]() $h\in \mathfrak{a}$
and thus part (c) holds.
$h\in \mathfrak{a}$
and thus part (c) holds.
If
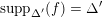 $\text{supp}_{\unicode[STIX]{x1D6E5}^{\prime }}(f)=\unicode[STIX]{x1D6E5}^{\prime }$
, then we set
$\text{supp}_{\unicode[STIX]{x1D6E5}^{\prime }}(f)=\unicode[STIX]{x1D6E5}^{\prime }$
, then we set
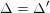 $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}^{\prime }$
; in this case we have
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}^{\prime }$
; in this case we have
![]() $h-S$
is central and part (d) holds vacuously. Now suppose
$h-S$
is central and part (d) holds vacuously. Now suppose
 $\text{supp}_{\unicode[STIX]{x1D6E5}^{\prime }}\left(f\right)\subsetneq \unicode[STIX]{x1D6E5}^{\prime }$
. Then we will show how to modify
$\text{supp}_{\unicode[STIX]{x1D6E5}^{\prime }}\left(f\right)\subsetneq \unicode[STIX]{x1D6E5}^{\prime }$
. Then we will show how to modify
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
to obtain a new system
$\unicode[STIX]{x1D6E5}^{\prime }$
to obtain a new system
![]() $\unicode[STIX]{x1D6E5}(\mathfrak{a,g})$
such that parts (a)–(d) are satisfied. For this let us write
$\unicode[STIX]{x1D6E5}(\mathfrak{a,g})$
such that parts (a)–(d) are satisfied. For this let us write
 $$\begin{eqnarray}Z=S-h,\quad Z^{\prime }=S^{\prime }-h,\quad h_{\unicode[STIX]{x1D700}}=Z+\unicode[STIX]{x1D700}Z^{\prime }+\unicode[STIX]{x1D700}^{2}h,\end{eqnarray}$$
$$\begin{eqnarray}Z=S-h,\quad Z^{\prime }=S^{\prime }-h,\quad h_{\unicode[STIX]{x1D700}}=Z+\unicode[STIX]{x1D700}Z^{\prime }+\unicode[STIX]{x1D700}^{2}h,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D700}>0$
is chosen sufficiently small so that for all
$\unicode[STIX]{x1D700}>0$
is chosen sufficiently small so that for all
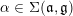 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
we have
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}(Z)>0 & \;\Longrightarrow \; & \displaystyle \unicode[STIX]{x1D6FC}(Z)>\unicode[STIX]{x1D700}|\unicode[STIX]{x1D6FC}(Z^{\prime })|+\unicode[STIX]{x1D700}^{2}|\unicode[STIX]{x1D6FC}(h)|,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}(Z)>0 & \;\Longrightarrow \; & \displaystyle \unicode[STIX]{x1D6FC}(Z)>\unicode[STIX]{x1D700}|\unicode[STIX]{x1D6FC}(Z^{\prime })|+\unicode[STIX]{x1D700}^{2}|\unicode[STIX]{x1D6FC}(h)|,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}(Z^{\prime })>0 & \;\Longrightarrow \; & \displaystyle \unicode[STIX]{x1D6FC}(Z^{\prime })>\unicode[STIX]{x1D700}|\unicode[STIX]{x1D6FC}(h)|.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}(Z^{\prime })>0 & \;\Longrightarrow \; & \displaystyle \unicode[STIX]{x1D6FC}(Z^{\prime })>\unicode[STIX]{x1D700}|\unicode[STIX]{x1D6FC}(h)|.\end{eqnarray}$$
We claim that
![]() $h_{\unicode[STIX]{x1D700}}$
is regular in the sense that
$h_{\unicode[STIX]{x1D700}}$
is regular in the sense that
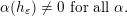 $\unicode[STIX]{x1D6FC}(h_{\unicode[STIX]{x1D700}})\neq 0\text{ for all }\unicode[STIX]{x1D6FC}.$
If
$\unicode[STIX]{x1D6FC}(h_{\unicode[STIX]{x1D700}})\neq 0\text{ for all }\unicode[STIX]{x1D6FC}.$
If
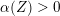 $\unicode[STIX]{x1D6FC}(Z)>0$
this follows from (22), if
$\unicode[STIX]{x1D6FC}(Z)>0$
this follows from (22), if
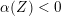 $\unicode[STIX]{x1D6FC}(Z)<0$
, we simply replace
$\unicode[STIX]{x1D6FC}(Z)<0$
, we simply replace
![]() $\unicode[STIX]{x1D6FC}$
by
$\unicode[STIX]{x1D6FC}$
by
![]() $-\unicode[STIX]{x1D6FC}$
. If
$-\unicode[STIX]{x1D6FC}$
. If
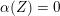 $\unicode[STIX]{x1D6FC}(Z)=0$
but
$\unicode[STIX]{x1D6FC}(Z)=0$
but
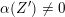 $\unicode[STIX]{x1D6FC}(Z^{\prime })\neq 0$
, then this follows analogously from (23). Finally, if
$\unicode[STIX]{x1D6FC}(Z^{\prime })\neq 0$
, then this follows analogously from (23). Finally, if
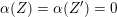 $\unicode[STIX]{x1D6FC}(Z)=\unicode[STIX]{x1D6FC}(Z^{\prime })=0$
, then
$\unicode[STIX]{x1D6FC}(Z)=\unicode[STIX]{x1D6FC}(Z^{\prime })=0$
, then
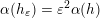 $\unicode[STIX]{x1D6FC}(h_{\unicode[STIX]{x1D700}})=\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FC}(h)$
and we must show that
$\unicode[STIX]{x1D6FC}(h_{\unicode[STIX]{x1D700}})=\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FC}(h)$
and we must show that
 $\unicode[STIX]{x1D6FC}(h)\neq 0$
, but this follows from the regularity of
$\unicode[STIX]{x1D6FC}(h)\neq 0$
, but this follows from the regularity of
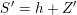 $S^{\prime }=h+Z^{\prime }$
.
$S^{\prime }=h+Z^{\prime }$
.
This means that we can define a positive root system as follows
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}\mid \unicode[STIX]{x1D6FC}(h_{\unicode[STIX]{x1D700}})>0\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}\mid \unicode[STIX]{x1D6FC}(h_{\unicode[STIX]{x1D700}})>0\}.\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D6E5}$
be the corresponding simple system; we will show that
$\unicode[STIX]{x1D6E5}$
be the corresponding simple system; we will show that
 $\text{supp}_{\unicode[STIX]{x1D6E5}^{\prime }}(f)\subset \unicode[STIX]{x1D6E5}.$
This implies that
$\text{supp}_{\unicode[STIX]{x1D6E5}^{\prime }}(f)\subset \unicode[STIX]{x1D6E5}.$
This implies that
![]() $\unicode[STIX]{x1D6E5}$
is compatible with
$\unicode[STIX]{x1D6E5}$
is compatible with
![]() $e$
, so that part (a) holds. To prove that
$e$
, so that part (a) holds. To prove that
 $\text{supp}_{\unicode[STIX]{x1D6E5}^{\prime }}(f)\subset \unicode[STIX]{x1D6E5}$
suppose
$\text{supp}_{\unicode[STIX]{x1D6E5}^{\prime }}(f)\subset \unicode[STIX]{x1D6E5}$
suppose
![]() $\unicode[STIX]{x1D6FC}$
belongs to
$\unicode[STIX]{x1D6FC}$
belongs to
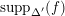 $\text{supp}_{\unicode[STIX]{x1D6E5}^{\prime }}(f)$
. Then we have
$\text{supp}_{\unicode[STIX]{x1D6E5}^{\prime }}(f)$
. Then we have
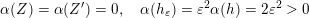 $\unicode[STIX]{x1D6FC}(Z)=\unicode[STIX]{x1D6FC}(Z^{\prime })=0,\quad \unicode[STIX]{x1D6FC}(h_{\unicode[STIX]{x1D700}})=\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FC}(h)=2\unicode[STIX]{x1D700}^{2}>0$
. This means that
$\unicode[STIX]{x1D6FC}(Z)=\unicode[STIX]{x1D6FC}(Z^{\prime })=0,\quad \unicode[STIX]{x1D6FC}(h_{\unicode[STIX]{x1D700}})=\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FC}(h)=2\unicode[STIX]{x1D700}^{2}>0$
. This means that
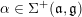 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})$
and it remains to show that we cannot write
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})$
and it remains to show that we cannot write
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}\end{eqnarray}$$
where
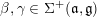 $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})$
. Now if
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})$
. Now if
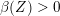 $\unicode[STIX]{x1D6FD}(Z)>0$
or
$\unicode[STIX]{x1D6FD}(Z)>0$
or
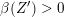 $\unicode[STIX]{x1D6FD}(Z^{\prime })>0$
, then (24) is impossible by (22) and (23). Thus, we may assume
$\unicode[STIX]{x1D6FD}(Z^{\prime })>0$
, then (24) is impossible by (22) and (23). Thus, we may assume
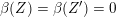 $\unicode[STIX]{x1D6FD}(Z)=\unicode[STIX]{x1D6FD}(Z^{\prime })=0$
and thus
$\unicode[STIX]{x1D6FD}(Z)=\unicode[STIX]{x1D6FD}(Z^{\prime })=0$
and thus
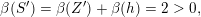 $\unicode[STIX]{x1D6FD}(S^{\prime })=\unicode[STIX]{x1D6FD}(Z^{\prime })+\unicode[STIX]{x1D6FD}(h)=2>0,$
and similarly
$\unicode[STIX]{x1D6FD}(S^{\prime })=\unicode[STIX]{x1D6FD}(Z^{\prime })+\unicode[STIX]{x1D6FD}(h)=2>0,$
and similarly
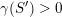 $\unicode[STIX]{x1D6FE}(S^{\prime })>0$
. But
$\unicode[STIX]{x1D6FE}(S^{\prime })>0$
. But
![]() $\unicode[STIX]{x1D6FC}$
is a simple root in the positive system defined by
$\unicode[STIX]{x1D6FC}$
is a simple root in the positive system defined by
![]() $S^{\prime }$
, so (24) cannot hold.
$S^{\prime }$
, so (24) cannot hold.
Finally we verify that
 $\unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})$
satisfies part (d). Thus suppose
$\unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})$
satisfies part (d). Thus suppose
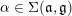 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
satisfies
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
satisfies
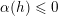 $\unicode[STIX]{x1D6FC}(h)\leqslant 0$
and
$\unicode[STIX]{x1D6FC}(h)\leqslant 0$
and
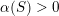 $\unicode[STIX]{x1D6FC}(S)>0$
, then we have
$\unicode[STIX]{x1D6FC}(S)>0$
, then we have
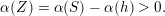 $\unicode[STIX]{x1D6FC}(Z)=\unicode[STIX]{x1D6FC}(S)-\unicode[STIX]{x1D6FC}(h)>0.$
By (22), this implies
$\unicode[STIX]{x1D6FC}(Z)=\unicode[STIX]{x1D6FC}(S)-\unicode[STIX]{x1D6FC}(h)>0.$
By (22), this implies
 $\unicode[STIX]{x1D6FC}(h_{\unicode[STIX]{x1D700}})=\unicode[STIX]{x1D6FC}(Z)+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}(Z^{\prime })+\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FC}(h)>0$
. Thus, we have
$\unicode[STIX]{x1D6FC}(h_{\unicode[STIX]{x1D700}})=\unicode[STIX]{x1D6FC}(Z)+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}(Z^{\prime })+\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FC}(h)>0$
. Thus, we have
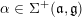 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})$
as desired.◻
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}^{+}(\mathfrak{a,g})$
as desired.◻
Proposition 3.3.4. Suppose that
![]() $\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
can be completed to a principal Whittaker pair. Then any degenerate Whittaker model
$\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
can be completed to a principal Whittaker pair. Then any degenerate Whittaker model
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
can be mapped onto some principal degenerate Whittaker model
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
can be mapped onto some principal degenerate Whittaker model
![]() ${\mathcal{W}}_{\widetilde{S},\unicode[STIX]{x1D711}}$
.
${\mathcal{W}}_{\widetilde{S},\unicode[STIX]{x1D711}}$
.
Proof. By Corollary 3.0.5 it suffices to find a maximally split toral subalgebra
![]() $\mathfrak{a}$
and containing a neutral element
$\mathfrak{a}$
and containing a neutral element
![]() $h$
for
$h$
for
![]() $\unicode[STIX]{x1D711}$
, and a principal element
$\unicode[STIX]{x1D711}$
, and a principal element
![]() $\tilde{S}$
such that
$\tilde{S}$
such that
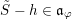 $\tilde{S}-h\in \mathfrak{a}_{\unicode[STIX]{x1D711}}$
and
$\tilde{S}-h\in \mathfrak{a}_{\unicode[STIX]{x1D711}}$
and
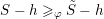 $S-h\geqslant _{\unicode[STIX]{x1D711}}\tilde{S}-h$
in the sense of Definition 3.0.4, i.e.
$S-h\geqslant _{\unicode[STIX]{x1D711}}\tilde{S}-h$
in the sense of Definition 3.0.4, i.e.
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}(h)\leqslant 0\quad \text{and}\quad \unicode[STIX]{x1D6FC}(S)\geqslant 1\;\Longrightarrow \;\unicode[STIX]{x1D6FC}(\tilde{S})\geqslant 1\quad \text{for all }\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}(\mathfrak{a,g}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}(h)\leqslant 0\quad \text{and}\quad \unicode[STIX]{x1D6FC}(S)\geqslant 1\;\Longrightarrow \;\unicode[STIX]{x1D6FC}(\tilde{S})\geqslant 1\quad \text{for all }\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}(\mathfrak{a,g}).\end{eqnarray}$$
Let
![]() $f\in \mathfrak{g}$
be the nilpotent element corresponding to
$f\in \mathfrak{g}$
be the nilpotent element corresponding to
![]() $\unicode[STIX]{x1D711}$
. Then
$\unicode[STIX]{x1D711}$
. Then
![]() $(S,f)$
satisfies the conditions of Proposition 3.3.3. Let
$(S,f)$
satisfies the conditions of Proposition 3.3.3. Let
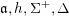 $\mathfrak{a},h,\unicode[STIX]{x1D6F4}^{+},\unicode[STIX]{x1D6E5}$
be as in the proposition, and let
$\mathfrak{a},h,\unicode[STIX]{x1D6F4}^{+},\unicode[STIX]{x1D6E5}$
be as in the proposition, and let
 $\tilde{S}=S_{\unicode[STIX]{x1D6E5}}$
. Then any
$\tilde{S}=S_{\unicode[STIX]{x1D6E5}}$
. Then any
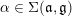 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
with
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F4}(\mathfrak{a,g})$
with
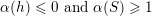 $\unicode[STIX]{x1D6FC}(h)\leqslant 0\text{ and }\unicode[STIX]{x1D6FC}(S)\geqslant 1$
lies in
$\unicode[STIX]{x1D6FC}(h)\leqslant 0\text{ and }\unicode[STIX]{x1D6FC}(S)\geqslant 1$
lies in
![]() $\unicode[STIX]{x1D6F4}^{+}$
. Since
$\unicode[STIX]{x1D6F4}^{+}$
. Since
![]() $\tilde{S}$
is principal, we deduce that
$\tilde{S}$
is principal, we deduce that
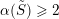 $\unicode[STIX]{x1D6FC}(\tilde{S})\geqslant 2$
.◻
$\unicode[STIX]{x1D6FC}(\tilde{S})\geqslant 2$
.◻
3.3.1 Archimedean case
For a smooth representation
![]() $\unicode[STIX]{x1D70B}$
of a real reductive group
$\unicode[STIX]{x1D70B}$
of a real reductive group
![]() $G$
one can define one more invariant, which we denote
$G$
one can define one more invariant, which we denote
![]() ${\mathcal{V}}(\unicode[STIX]{x1D70B})$
and call the annihilator variety of
${\mathcal{V}}(\unicode[STIX]{x1D70B})$
and call the annihilator variety of
![]() $\unicode[STIX]{x1D70B}$
. It is sometimes called the associated variety of the annihilator of
$\unicode[STIX]{x1D70B}$
. It is sometimes called the associated variety of the annihilator of
![]() $\unicode[STIX]{x1D70B}$
. It is defined to be the set of zeros in
$\unicode[STIX]{x1D70B}$
. It is defined to be the set of zeros in
![]() $\mathfrak{g}_{\mathbb{C}}^{\ast }$
of the ideal in the symmetric algebra
$\mathfrak{g}_{\mathbb{C}}^{\ast }$
of the ideal in the symmetric algebra
![]() $S(\mathfrak{g}_{\mathbb{C}})$
, which is generated by the symbols of the annihilator ideal of
$S(\mathfrak{g}_{\mathbb{C}})$
, which is generated by the symbols of the annihilator ideal of
![]() $\unicode[STIX]{x1D70B}$
in the universal enveloping algebra
$\unicode[STIX]{x1D70B}$
in the universal enveloping algebra
![]() $U(\mathfrak{g}_{\mathbb{C}})$
. It follows from [Reference VoganVog91, Theorem 8.4] and [Reference Schmid and VilonenSV00] that
$U(\mathfrak{g}_{\mathbb{C}})$
. It follows from [Reference VoganVog91, Theorem 8.4] and [Reference Schmid and VilonenSV00] that
![]() ${\mathcal{V}}(\unicode[STIX]{x1D70B})$
is the Zariski closure of
${\mathcal{V}}(\unicode[STIX]{x1D70B})$
is the Zariski closure of
![]() $\operatorname{WF}(\unicode[STIX]{x1D70B})$
in
$\operatorname{WF}(\unicode[STIX]{x1D70B})$
in
![]() $\mathfrak{g}_{\mathbb{C}}^{\ast }$
. Note that if
$\mathfrak{g}_{\mathbb{C}}^{\ast }$
. Note that if
![]() $G$
is a complex reductive group or
$G$
is a complex reductive group or
 $G=\text{GL}_{n}(\mathbb{R})$
we have
$G=\text{GL}_{n}(\mathbb{R})$
we have
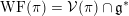 $\operatorname{WF}(\unicode[STIX]{x1D70B})={\mathcal{V}}(\unicode[STIX]{x1D70B})\cap \mathfrak{g}^{\ast }$
.
$\operatorname{WF}(\unicode[STIX]{x1D70B})={\mathcal{V}}(\unicode[STIX]{x1D70B})\cap \mathfrak{g}^{\ast }$
.
We will use the following theorems.
Theorem 3.3.5 [Reference MatumotoMat87, Corollary 4].
Let
![]() $\unicode[STIX]{x1D70B}$
be a smooth representation of
$\unicode[STIX]{x1D70B}$
be a smooth representation of
![]() $G$
, let
$G$
, let
![]() ${\mathcal{O}}\subset \mathfrak{g}^{\ast }$
be a nilpotent orbit and suppose that
${\mathcal{O}}\subset \mathfrak{g}^{\ast }$
be a nilpotent orbit and suppose that
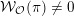 ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
. Then
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
. Then
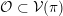 ${\mathcal{O}}\subset {\mathcal{V}}(\unicode[STIX]{x1D70B})$
.
${\mathcal{O}}\subset {\mathcal{V}}(\unicode[STIX]{x1D70B})$
.
Theorem 3.3.6 [Reference Gourevitch and SahiGS15, Theorem B].
Let
![]() $(S,\unicode[STIX]{x1D711})$
be a principal degenerate Whittaker pair for
$(S,\unicode[STIX]{x1D711})$
be a principal degenerate Whittaker pair for
![]() $G$
. Let
$G$
. Let
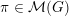 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
such that
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
such that
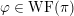 $\unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})$
. Then:
$\unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})$
. Then:
-
(i) if
 $G$
is a complex group or
$G$
is a complex group or
 $G=\text{GL}_{n}(\mathbb{R})$
, then
$G=\text{GL}_{n}(\mathbb{R})$
, then
 ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0$
;
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0$
; -
(ii) if
 $G$
is quasisplit, then there exists
$G$
is quasisplit, then there exists
 $g\in G_{\mathbb{C}}$
such that
$g\in G_{\mathbb{C}}$
such that
 $\text{ad}(g)$
preserves
$\text{ad}(g)$
preserves
 $\mathfrak{g}$
and
$\mathfrak{g}$
and
 ${\mathcal{W}}_{\text{ad}(g)(S),\text{ad}(g)(\unicode[STIX]{x1D711})}(\unicode[STIX]{x1D70B})\neq 0$
.
${\mathcal{W}}_{\text{ad}(g)(S),\text{ad}(g)(\unicode[STIX]{x1D711})}(\unicode[STIX]{x1D70B})\neq 0$
.
In fact, the theorems in [Reference MatumotoMat87, Reference Gourevitch and SahiGS15] are stronger than the versions we state here.
Proof of Theorem B.
Let
![]() $(S,\unicode[STIX]{x1D711})$
be as in the theorem. Then
$(S,\unicode[STIX]{x1D711})$
be as in the theorem. Then
![]() $\unicode[STIX]{x1D711}$
can be completed to a principal Whittaker pair, and Proposition 3.3.4 implies that the degenerate Whittaker model
$\unicode[STIX]{x1D711}$
can be completed to a principal Whittaker pair, and Proposition 3.3.4 implies that the degenerate Whittaker model
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
can be mapped onto some principal degenerate Whittaker model
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
can be mapped onto some principal degenerate Whittaker model
![]() ${\mathcal{W}}_{\widetilde{S},\unicode[STIX]{x1D711}}$
. By Theorem A,
${\mathcal{W}}_{\widetilde{S},\unicode[STIX]{x1D711}}$
. By Theorem A,
![]() ${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
maps onto
${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
maps onto
![]() ${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
. Thus, we have
${\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
. Thus, we have
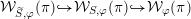 ${\mathcal{W}}_{\widetilde{S},\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}){\hookrightarrow}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}){\hookrightarrow}{\mathcal{W}}_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
. Together with Theorems 3.3.5 and 3.3.6 we get
${\mathcal{W}}_{\widetilde{S},\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}){\hookrightarrow}{\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}){\hookrightarrow}{\mathcal{W}}_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
. Together with Theorems 3.3.5 and 3.3.6 we get
 $$\begin{eqnarray}\unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})\Rightarrow {\mathcal{W}}_{\widetilde{S},\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0\Rightarrow {\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0\Rightarrow {\mathcal{W}}_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0\Rightarrow \unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B}).\square\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})\Rightarrow {\mathcal{W}}_{\widetilde{S},\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0\Rightarrow {\mathcal{W}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0\Rightarrow {\mathcal{W}}_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0\Rightarrow \unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B}).\square\end{eqnarray}$$
In the same way we get the following statement for real reductive groups.
Corollary 3.3.7. Suppose that
![]() $G$
is quasisplit and let
$G$
is quasisplit and let
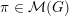 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
. Let
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
. Let
![]() $(S,\unicode[STIX]{x1D711})$
be a Whittaker pair such that
$(S,\unicode[STIX]{x1D711})$
be a Whittaker pair such that
![]() $\unicode[STIX]{x1D711}$
is a PL nilpotent. Suppose that
$\unicode[STIX]{x1D711}$
is a PL nilpotent. Suppose that
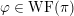 $\unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})$
. Then there exists
$\unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})$
. Then there exists
![]() $g\in G_{\mathbb{C}}$
such that
$g\in G_{\mathbb{C}}$
such that
![]() $\text{ad}(g)$
preserves
$\text{ad}(g)$
preserves
![]() $\mathfrak{g}$
and
$\mathfrak{g}$
and
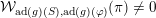 ${\mathcal{W}}_{\text{ad}(g)(S),\text{ad}(g)(\unicode[STIX]{x1D711})}(\unicode[STIX]{x1D70B})\neq 0$
.
${\mathcal{W}}_{\text{ad}(g)(S),\text{ad}(g)(\unicode[STIX]{x1D711})}(\unicode[STIX]{x1D70B})\neq 0$
.
4 General linear groups
4.1 Notation
Let us first introduce some notation. A composition
![]() $\unicode[STIX]{x1D702}$
of
$\unicode[STIX]{x1D702}$
of
![]() $n$
is a sequence of natural (positive) numbers
$n$
is a sequence of natural (positive) numbers
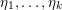 $\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{k}$
with
$\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{k}$
with
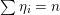 $\sum \unicode[STIX]{x1D702}_{i}=n$
. The length of
$\sum \unicode[STIX]{x1D702}_{i}=n$
. The length of
![]() $\unicode[STIX]{x1D702}$
is
$\unicode[STIX]{x1D702}$
is
![]() $k$
. A partition
$k$
. A partition
![]() $\unicode[STIX]{x1D706}$
is a composition such that
$\unicode[STIX]{x1D706}$
is a composition such that
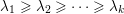 $\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{k}$
. For a composition
$\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{k}$
. For a composition
![]() $\unicode[STIX]{x1D702}$
we denote by
$\unicode[STIX]{x1D702}$
we denote by
![]() $\unicode[STIX]{x1D702}^{{\geqslant}}$
the corresponding partition. A partial order on partitions of
$\unicode[STIX]{x1D702}^{{\geqslant}}$
the corresponding partition. A partial order on partitions of
![]() $n$
is defined by
$n$
is defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}\quad \text{if }\mathop{\sum }_{i=1}^{j}\unicode[STIX]{x1D706}_{i}\geqslant \mathop{\sum }_{i=1}^{j}\unicode[STIX]{x1D707}_{i}\quad \text{for any }1\leqslant j\leqslant \text{length}(\unicode[STIX]{x1D706}),\text{length}(\unicode[STIX]{x1D707}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}\quad \text{if }\mathop{\sum }_{i=1}^{j}\unicode[STIX]{x1D706}_{i}\geqslant \mathop{\sum }_{i=1}^{j}\unicode[STIX]{x1D707}_{i}\quad \text{for any }1\leqslant j\leqslant \text{length}(\unicode[STIX]{x1D706}),\text{length}(\unicode[STIX]{x1D707}).\end{eqnarray}$$
We will use the notation
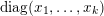 $\text{diag}(x_{1},\ldots ,x_{k})$
for diagonal and block-diagonal matrices. For a natural number
$\text{diag}(x_{1},\ldots ,x_{k})$
for diagonal and block-diagonal matrices. For a natural number
![]() $k$
we denote by
$k$
we denote by
![]() $J_{k}\in \mathfrak{g}_{k}$
the lower-triangular Jordan block of size
$J_{k}\in \mathfrak{g}_{k}$
the lower-triangular Jordan block of size
![]() $k$
, and by
$k$
, and by
![]() $h_{k}$
the diagonal matrix
$h_{k}$
the diagonal matrix
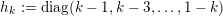 $h_{k}:=\text{diag}(k-1,k-3,\ldots ,1-k)$
. For a composition
$h_{k}:=\text{diag}(k-1,k-3,\ldots ,1-k)$
. For a composition
![]() $\unicode[STIX]{x1D702}$
we denote
$\unicode[STIX]{x1D702}$
we denote
 $$\begin{eqnarray}J_{\unicode[STIX]{x1D702}}:=\text{diag}(J_{\unicode[STIX]{x1D702}_{1}},\ldots ,J_{\unicode[STIX]{x1D702}_{k}})\in \mathfrak{g}_{n}\quad \text{and}\quad h_{\unicode[STIX]{x1D702}}:=\text{diag}(h_{\unicode[STIX]{x1D702}_{1}},\ldots ,h_{\unicode[STIX]{x1D702}_{k}})\in \mathfrak{g}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}J_{\unicode[STIX]{x1D702}}:=\text{diag}(J_{\unicode[STIX]{x1D702}_{1}},\ldots ,J_{\unicode[STIX]{x1D702}_{k}})\in \mathfrak{g}_{n}\quad \text{and}\quad h_{\unicode[STIX]{x1D702}}:=\text{diag}(h_{\unicode[STIX]{x1D702}_{1}},\ldots ,h_{\unicode[STIX]{x1D702}_{k}})\in \mathfrak{g}_{n}.\end{eqnarray}$$
Note that
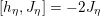 $[h_{\unicode[STIX]{x1D702}},J_{\unicode[STIX]{x1D702}}]=-2J_{\unicode[STIX]{x1D702}}$
and
$[h_{\unicode[STIX]{x1D702}},J_{\unicode[STIX]{x1D702}}]=-2J_{\unicode[STIX]{x1D702}}$
and
![]() $(J_{\unicode[STIX]{x1D702}},h_{\unicode[STIX]{x1D702}})$
can be completed to an
$(J_{\unicode[STIX]{x1D702}},h_{\unicode[STIX]{x1D702}})$
can be completed to an
![]() $\mathfrak{sl}_{2}$
-triple.
$\mathfrak{sl}_{2}$
-triple.
Identify
![]() $\mathfrak{g}_{n}^{\ast }$
with
$\mathfrak{g}_{n}^{\ast }$
with
![]() $\mathfrak{g}_{n}$
using the trace form. Denote by
$\mathfrak{g}_{n}$
using the trace form. Denote by
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
the orbit of
${\mathcal{O}}_{\unicode[STIX]{x1D702}}$
the orbit of
![]() $J_{\unicode[STIX]{x1D702}}$
, and also the corresponding orbit in
$J_{\unicode[STIX]{x1D702}}$
, and also the corresponding orbit in
![]() $\mathfrak{g}_{n}^{\ast }$
. By the Jordan theorem all nilpotent orbits are of this form. It is well known that
$\mathfrak{g}_{n}^{\ast }$
. By the Jordan theorem all nilpotent orbits are of this form. It is well known that
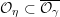 ${\mathcal{O}}_{\unicode[STIX]{x1D702}}\subset \overline{{\mathcal{O}}_{\unicode[STIX]{x1D6FE}}}$
if and only if
${\mathcal{O}}_{\unicode[STIX]{x1D702}}\subset \overline{{\mathcal{O}}_{\unicode[STIX]{x1D6FE}}}$
if and only if
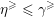 $\unicode[STIX]{x1D702}^{{\geqslant}}\leqslant \unicode[STIX]{x1D6FE}^{{\geqslant}}$
. Let
$\unicode[STIX]{x1D702}^{{\geqslant}}\leqslant \unicode[STIX]{x1D6FE}^{{\geqslant}}$
. Let
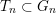 $T_{n}\subset G_{n}$
denote the subgroup of diagonal matrices and
$T_{n}\subset G_{n}$
denote the subgroup of diagonal matrices and
![]() $\mathfrak{t}_{n}\subset \mathfrak{g}_{n}$
the subalgebra of diagonal matrices.
$\mathfrak{t}_{n}\subset \mathfrak{g}_{n}$
the subalgebra of diagonal matrices.
4.2 Proof of Theorem D
Let
![]() $E_{ij}$
denote the elementary matrix with 1 in the
$E_{ij}$
denote the elementary matrix with 1 in the
![]() $(i,j)$
entry and zeros elsewhere.
$(i,j)$
entry and zeros elsewhere.
Lemma 4.2.1. For any
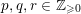 $p,q,r\in \mathbb{Z}_{{\geqslant}0}$
with
$p,q,r\in \mathbb{Z}_{{\geqslant}0}$
with
![]() $p\geqslant r$
there exists a diagonal matrix
$p\geqslant r$
there exists a diagonal matrix
 $S\in \mathfrak{t}_{m}(\mathbb{Z}),$
where
$S\in \mathfrak{t}_{m}(\mathbb{Z}),$
where
 $m=p+q+r$
, and a regular nilpotent
$m=p+q+r$
, and a regular nilpotent
 $X\in \mathfrak{g}_{q+r}$
such that
$X\in \mathfrak{g}_{q+r}$
such that
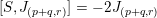 $[S,J_{(p+q,r)}]=-2J_{(p+q,r)}$
and
$[S,J_{(p+q,r)}]=-2J_{(p+q,r)}$
and
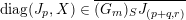 $\text{diag}(J_{p},X)\in \overline{(G_{m})_{S}J_{(p+q,r)}}$
.
$\text{diag}(J_{p},X)\in \overline{(G_{m})_{S}J_{(p+q,r)}}$
.
Proof. If
![]() $r=0$
or
$r=0$
or
![]() $q=0$
, we take
$q=0$
, we take
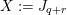 $X:=J_{q+r}$
,
$X:=J_{q+r}$
,
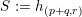 $S:=h_{(p+q,r)}$
and note that
$S:=h_{(p+q,r)}$
and note that
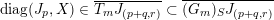 $\text{diag}(J_{p},X)\in \overline{T_{m}J_{(p+q,r)}}\subset \overline{(G_{m})_{S}J_{(p+q,r)}}$
. Assume now
$\text{diag}(J_{p},X)\in \overline{T_{m}J_{(p+q,r)}}\subset \overline{(G_{m})_{S}J_{(p+q,r)}}$
. Assume now
![]() $q,r>0$
and let
$q,r>0$
and let
 $$\begin{eqnarray}\displaystyle & F:=J_{(p+q,r)},\quad S:=\text{diag}(h_{p+q},h_{r}+(r+q-p)\text{Id}_{r})\in \mathfrak{g}_{m}, & \displaystyle \nonumber\\ \displaystyle & g:=(\text{Id}_{m}+E_{p-r+1,m-r+1})(\text{Id}_{m}+E_{p-r+2,m-r+2})\cdot \ldots \cdot (\text{Id}_{m}+E_{p,m})\in G_{m}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & F:=J_{(p+q,r)},\quad S:=\text{diag}(h_{p+q},h_{r}+(r+q-p)\text{Id}_{r})\in \mathfrak{g}_{m}, & \displaystyle \nonumber\\ \displaystyle & g:=(\text{Id}_{m}+E_{p-r+1,m-r+1})(\text{Id}_{m}+E_{p-r+2,m-r+2})\cdot \ldots \cdot (\text{Id}_{m}+E_{p,m})\in G_{m}. & \displaystyle \nonumber\end{eqnarray}$$
Note that
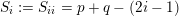 $S_{i}:=S_{ii}=p+q-(2i-1)$
for
$S_{i}:=S_{ii}=p+q-(2i-1)$
for
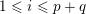 $1\leqslant i\leqslant p+q$
and
$1\leqslant i\leqslant p+q$
and
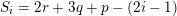 $S_{i}=2r+3q+p-(2i-1)$
for
$S_{i}=2r+3q+p-(2i-1)$
for
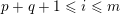 $p+q+1\leqslant i\leqslant m$
. Thus,
$p+q+1\leqslant i\leqslant m$
. Thus,
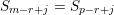 $S_{m-r+j}=S_{p-r+j}$
for
$S_{m-r+j}=S_{p-r+j}$
for
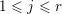 $1\leqslant j\leqslant r$
and thus
$1\leqslant j\leqslant r$
and thus
![]() $g$
commutes with
$g$
commutes with
![]() $S$
. Note also that
$S$
. Note also that
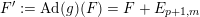 $F^{\prime }:=\text{Ad}(g)(F)=F+E_{p+1,m}$
. Conjugating
$F^{\prime }:=\text{Ad}(g)(F)=F+E_{p+1,m}$
. Conjugating
![]() $F^{\prime }$
by a suitable diagonal matrix we can obtain
$F^{\prime }$
by a suitable diagonal matrix we can obtain
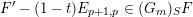 $F^{\prime }-(1-t)E_{p+1,p}\in (G_{m})_{S}F$
for any
$F^{\prime }-(1-t)E_{p+1,p}\in (G_{m})_{S}F$
for any
![]() $t\in \mathbb{F}^{\times }$
. Letting
$t\in \mathbb{F}^{\times }$
. Letting
![]() $t$
go to zero, we get that
$t$
go to zero, we get that
 $$\begin{eqnarray}f:=F^{\prime }-E_{p+1,p}=F+E_{p+1,m}-E_{p+1,p}\in \overline{(G_{m})_{S}F}.\end{eqnarray}$$
$$\begin{eqnarray}f:=F^{\prime }-E_{p+1,p}=F+E_{p+1,m}-E_{p+1,p}\in \overline{(G_{m})_{S}F}.\end{eqnarray}$$
Finally, it is easy to see that
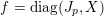 $f=\text{diag}(J_{p},X)$
for a regular nilpotent
$f=\text{diag}(J_{p},X)$
for a regular nilpotent
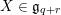 $X\in \mathfrak{g}_{q+r}$
.◻
$X\in \mathfrak{g}_{q+r}$
.◻
Lemma 4.2.2. Let
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}$
be partitions of
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}$
be partitions of
![]() $n$
with
$n$
with
![]() $\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}$
. Then there exists an index
$\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}$
. Then there exists an index
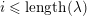 $i\leqslant \text{length}(\unicode[STIX]{x1D706})$
such that
$i\leqslant \text{length}(\unicode[STIX]{x1D706})$
such that
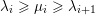 $\unicode[STIX]{x1D706}_{i}\geqslant \unicode[STIX]{x1D707}_{i}\geqslant \unicode[STIX]{x1D706}_{i+1}$
. Here, if
$\unicode[STIX]{x1D706}_{i}\geqslant \unicode[STIX]{x1D707}_{i}\geqslant \unicode[STIX]{x1D706}_{i+1}$
. Here, if
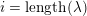 $i=\text{length}(\unicode[STIX]{x1D706})$
we take
$i=\text{length}(\unicode[STIX]{x1D706})$
we take
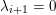 $\unicode[STIX]{x1D706}_{i+1}=0$
.
$\unicode[STIX]{x1D706}_{i+1}=0$
.
Proof. We prove by induction on
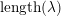 $\text{length}(\unicode[STIX]{x1D706})$
. If
$\text{length}(\unicode[STIX]{x1D706})$
. If
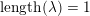 $\text{length}(\unicode[STIX]{x1D706})=1$
take
$\text{length}(\unicode[STIX]{x1D706})=1$
take
![]() $i=1$
. For the induction step, assume
$i=1$
. For the induction step, assume
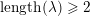 $\text{length}(\unicode[STIX]{x1D706})\geqslant 2$
and the lemma holds for all shorter partitions. If
$\text{length}(\unicode[STIX]{x1D706})\geqslant 2$
and the lemma holds for all shorter partitions. If
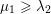 $\unicode[STIX]{x1D707}_{1}\geqslant \unicode[STIX]{x1D706}_{2}$
take
$\unicode[STIX]{x1D707}_{1}\geqslant \unicode[STIX]{x1D706}_{2}$
take
![]() $i:=1$
. Otherwise, consider the partitions
$i:=1$
. Otherwise, consider the partitions
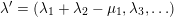 $\unicode[STIX]{x1D706}^{\prime }=(\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}-\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D706}_{3},\ldots )$
and
$\unicode[STIX]{x1D706}^{\prime }=(\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}-\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D706}_{3},\ldots )$
and
 $\unicode[STIX]{x1D707}^{\prime }=(\unicode[STIX]{x1D707}_{2},\unicode[STIX]{x1D707}_{3},\ldots )$
. Note that these are indeed partitions and
$\unicode[STIX]{x1D707}^{\prime }=(\unicode[STIX]{x1D707}_{2},\unicode[STIX]{x1D707}_{3},\ldots )$
. Note that these are indeed partitions and
![]() $\unicode[STIX]{x1D706}^{\prime }\geqslant \unicode[STIX]{x1D707}^{\prime }$
. Thus, by the induction hypothesis there exists
$\unicode[STIX]{x1D706}^{\prime }\geqslant \unicode[STIX]{x1D707}^{\prime }$
. Thus, by the induction hypothesis there exists
![]() $j$
such that
$j$
such that
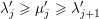 $\unicode[STIX]{x1D706}_{j}^{\prime }\geqslant \unicode[STIX]{x1D707}_{j}^{\prime }\geqslant \unicode[STIX]{x1D706}_{j+1}^{\prime }$
. If
$\unicode[STIX]{x1D706}_{j}^{\prime }\geqslant \unicode[STIX]{x1D707}_{j}^{\prime }\geqslant \unicode[STIX]{x1D706}_{j+1}^{\prime }$
. If
![]() $j>1$
, take
$j>1$
, take
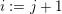 $i:=j+1$
. If
$i:=j+1$
. If
![]() $j=1$
, then
$j=1$
, then
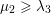 $\unicode[STIX]{x1D707}_{2}\geqslant \unicode[STIX]{x1D706}_{3}$
and we also have
$\unicode[STIX]{x1D707}_{2}\geqslant \unicode[STIX]{x1D706}_{3}$
and we also have
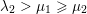 $\unicode[STIX]{x1D706}_{2}>\unicode[STIX]{x1D707}_{1}\geqslant \unicode[STIX]{x1D707}_{2}$
. Thus, we can take
$\unicode[STIX]{x1D706}_{2}>\unicode[STIX]{x1D707}_{1}\geqslant \unicode[STIX]{x1D707}_{2}$
. Thus, we can take
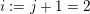 $i:=j+1=2$
in this case as well.◻
$i:=j+1=2$
in this case as well.◻
We are now ready to prove Theorem D. Let us reformulate it in terms of partitions.
Theorem 4.2.3. Let
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}$
be partitions of
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}$
be partitions of
![]() $n$
. Then
$n$
. Then
![]() $\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}$
if and only if there exists
$\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}$
if and only if there exists
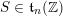 $S\in \mathfrak{t}_{n}(\mathbb{Z})$
such that
$S\in \mathfrak{t}_{n}(\mathbb{Z})$
such that
 $[S,J_{\unicode[STIX]{x1D706}}]=-2J_{\unicode[STIX]{x1D706}}$
and
$[S,J_{\unicode[STIX]{x1D706}}]=-2J_{\unicode[STIX]{x1D706}}$
and
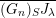 $\overline{(G_{n})_{S}J_{\unicode[STIX]{x1D706}}}$
intersects
$\overline{(G_{n})_{S}J_{\unicode[STIX]{x1D706}}}$
intersects
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D707}}$
.
${\mathcal{O}}_{\unicode[STIX]{x1D707}}$
.
Proof. We prove the lemma by induction on
![]() $n$
. The base case
$n$
. The base case
![]() $n=1$
is obvious. For the induction step, assume that the lemma holds for all
$n=1$
is obvious. For the induction step, assume that the lemma holds for all
![]() $n^{\prime }<n$
. By Lemma 4.2.2 there exists an index
$n^{\prime }<n$
. By Lemma 4.2.2 there exists an index
![]() $i$
with
$i$
with
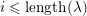 $i\leqslant \text{length}(\unicode[STIX]{x1D706})$
such that
$i\leqslant \text{length}(\unicode[STIX]{x1D706})$
such that
 $\unicode[STIX]{x1D706}_{i}\geqslant \unicode[STIX]{x1D707}_{i}\geqslant \unicode[STIX]{x1D706}_{i+1}$
. Let
$\unicode[STIX]{x1D706}_{i}\geqslant \unicode[STIX]{x1D707}_{i}\geqslant \unicode[STIX]{x1D706}_{i+1}$
. Let
 $$\begin{eqnarray}r:=\unicode[STIX]{x1D706}_{i+1},\quad q:=\unicode[STIX]{x1D707}_{i}-\unicode[STIX]{x1D706}_{i+1},\quad p:=\unicode[STIX]{x1D706}_{i}+\unicode[STIX]{x1D706}_{i+1}-\unicode[STIX]{x1D707}_{i}\quad \text{and}\quad m:=\unicode[STIX]{x1D706}_{i}+\unicode[STIX]{x1D706}_{i+1}.\end{eqnarray}$$
$$\begin{eqnarray}r:=\unicode[STIX]{x1D706}_{i+1},\quad q:=\unicode[STIX]{x1D707}_{i}-\unicode[STIX]{x1D706}_{i+1},\quad p:=\unicode[STIX]{x1D706}_{i}+\unicode[STIX]{x1D706}_{i+1}-\unicode[STIX]{x1D707}_{i}\quad \text{and}\quad m:=\unicode[STIX]{x1D706}_{i}+\unicode[STIX]{x1D706}_{i+1}.\end{eqnarray}$$
Now consider the partition
![]() $\unicode[STIX]{x1D706}^{\prime }$
obtained by replacing the blocks
$\unicode[STIX]{x1D706}^{\prime }$
obtained by replacing the blocks
![]() $\unicode[STIX]{x1D706}_{i}$
and
$\unicode[STIX]{x1D706}_{i}$
and
![]() $\unicode[STIX]{x1D706}_{i+1}$
by a single block
$\unicode[STIX]{x1D706}_{i+1}$
by a single block
![]() $p$
, and the partition
$p$
, and the partition
![]() $\unicode[STIX]{x1D707}^{\prime }$
obtained from
$\unicode[STIX]{x1D707}^{\prime }$
obtained from
![]() $\unicode[STIX]{x1D707}$
by omitting the block
$\unicode[STIX]{x1D707}$
by omitting the block
![]() $\unicode[STIX]{x1D707}_{i}$
. Note that both are indeed partitions of
$\unicode[STIX]{x1D707}_{i}$
. Note that both are indeed partitions of
![]() $n-\unicode[STIX]{x1D707}_{i}$
and that
$n-\unicode[STIX]{x1D707}_{i}$
and that
![]() $\unicode[STIX]{x1D706}^{\prime }\geqslant \unicode[STIX]{x1D707}^{\prime }$
. Thus, by the induction hypothesis there exists
$\unicode[STIX]{x1D706}^{\prime }\geqslant \unicode[STIX]{x1D707}^{\prime }$
. Thus, by the induction hypothesis there exists
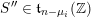 $S^{\prime \prime }\in \mathfrak{t}_{n-\unicode[STIX]{x1D707}_{i}}(\mathbb{Z})$
such that
$S^{\prime \prime }\in \mathfrak{t}_{n-\unicode[STIX]{x1D707}_{i}}(\mathbb{Z})$
such that
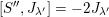 $[S^{\prime \prime },J_{\unicode[STIX]{x1D706}^{\prime }}]=-2J_{\unicode[STIX]{x1D706}^{\prime }}$
and
$[S^{\prime \prime },J_{\unicode[STIX]{x1D706}^{\prime }}]=-2J_{\unicode[STIX]{x1D706}^{\prime }}$
and
 $\overline{(G_{n-\unicode[STIX]{x1D707}_{i}})_{S^{\prime \prime }}J_{\unicode[STIX]{x1D706}^{\prime }}}$
intersects
$\overline{(G_{n-\unicode[STIX]{x1D707}_{i}})_{S^{\prime \prime }}J_{\unicode[STIX]{x1D706}^{\prime }}}$
intersects
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D707}^{\prime }}$
. Choose
${\mathcal{O}}_{\unicode[STIX]{x1D707}^{\prime }}$
. Choose
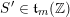 $S^{\prime }\in \mathfrak{t}_{m}(\mathbb{Z})$
and
$S^{\prime }\in \mathfrak{t}_{m}(\mathbb{Z})$
and
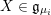 $X\in \mathfrak{g}_{\unicode[STIX]{x1D707}_{i}}$
using Lemma 4.2.1. Consider the matrix
$X\in \mathfrak{g}_{\unicode[STIX]{x1D707}_{i}}$
using Lemma 4.2.1. Consider the matrix
![]() $Z^{\prime }$
formed by taking the first
$Z^{\prime }$
formed by taking the first
![]() $p$
elements on the diagonal of
$p$
elements on the diagonal of
![]() $S^{\prime }$
and the matrix
$S^{\prime }$
and the matrix
![]() $Z^{\prime \prime }$
formed by taking the
$Z^{\prime \prime }$
formed by taking the
![]() $p$
elements number
$p$
elements number
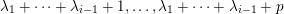 $\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{i-1}+1,\ldots ,\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{i-1}+p$
on the diagonal of
$\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{i-1}+1,\ldots ,\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{i-1}+p$
on the diagonal of
![]() $S^{\prime \prime }$
. Note that
$S^{\prime \prime }$
. Note that
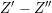 $Z^{\prime }-Z^{\prime \prime }$
is a diagonal matrix that commutes with
$Z^{\prime }-Z^{\prime \prime }$
is a diagonal matrix that commutes with
![]() $J_{p}$
and thus equals
$J_{p}$
and thus equals
![]() $c\text{Id}_{p}$
for some integer
$c\text{Id}_{p}$
for some integer
![]() $c$
. Replacing
$c$
. Replacing
![]() $S^{\prime }$
by
$S^{\prime }$
by
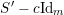 $S^{\prime }-c\text{Id}_{m}$
we can assume that
$S^{\prime }-c\text{Id}_{m}$
we can assume that
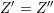 $Z^{\prime }=Z^{\prime \prime }$
and thus there exists
$Z^{\prime }=Z^{\prime \prime }$
and thus there exists
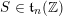 $S\in \mathfrak{t}_{n}(\mathbb{Z})$
that includes both
$S\in \mathfrak{t}_{n}(\mathbb{Z})$
that includes both
![]() $S^{\prime }$
and
$S^{\prime }$
and
![]() $S^{\prime \prime }$
as diagonal submatrices.
$S^{\prime \prime }$
as diagonal submatrices.
Let us show that
![]() $S$
satisfies the conditions of the lemma. Let
$S$
satisfies the conditions of the lemma. Let
 $a:=\sum _{j=1}^{i-1}\unicode[STIX]{x1D706}_{j}$
and
$a:=\sum _{j=1}^{i-1}\unicode[STIX]{x1D706}_{j}$
and
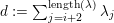 $d:=\sum _{j=i+2}^{\text{length}(\unicode[STIX]{x1D706})}\unicode[STIX]{x1D706}_{j}$
. Define an embedding of
$d:=\sum _{j=i+2}^{\text{length}(\unicode[STIX]{x1D706})}\unicode[STIX]{x1D706}_{j}$
. Define an embedding of
![]() $G_{m}$
into
$G_{m}$
into
![]() $G_{n}$
by
$G_{n}$
by
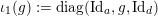 $\unicode[STIX]{x1D704}_{1}(g):=\text{diag}(\text{Id}_{a},g,\text{Id}_{d})$
. Define an embedding of
$\unicode[STIX]{x1D704}_{1}(g):=\text{diag}(\text{Id}_{a},g,\text{Id}_{d})$
. Define an embedding of
![]() $G_{n-\unicode[STIX]{x1D707}_{i}}$
into
$G_{n-\unicode[STIX]{x1D707}_{i}}$
into
![]() $G_{n}$
by
$G_{n}$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{2}\left(\begin{array}{@{}cc@{}}A & B\\ C & D\end{array}\right):=\left(\begin{array}{@{}ccc@{}}A & 0 & B\\ 0 & \text{Id}_{\unicode[STIX]{x1D707}_{i}} & 0\\ C & 0 & D\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{2}\left(\begin{array}{@{}cc@{}}A & B\\ C & D\end{array}\right):=\left(\begin{array}{@{}ccc@{}}A & 0 & B\\ 0 & \text{Id}_{\unicode[STIX]{x1D707}_{i}} & 0\\ C & 0 & D\end{array}\right),\end{eqnarray}$$
where
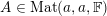 $A\in \text{Mat}(a,a,\mathbb{F})$
,
$A\in \text{Mat}(a,a,\mathbb{F})$
,
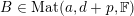 $B\in \text{Mat}(a,d+p,\mathbb{F})$
,
$B\in \text{Mat}(a,d+p,\mathbb{F})$
,
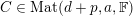 $C\in \text{Mat}(d+p,a,\mathbb{F})$
,
$C\in \text{Mat}(d+p,a,\mathbb{F})$
,
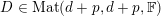 $D\in \text{Mat}(d+p,d+p,\mathbb{F})$
. Let
$D\in \text{Mat}(d+p,d+p,\mathbb{F})$
. Let
 $d\unicode[STIX]{x1D704}_{1}:\mathfrak{g}_{m}{\hookrightarrow}\mathfrak{g}_{n}$
and
$d\unicode[STIX]{x1D704}_{1}:\mathfrak{g}_{m}{\hookrightarrow}\mathfrak{g}_{n}$
and
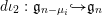 $d\unicode[STIX]{x1D704}_{2}:\mathfrak{g}_{n-\unicode[STIX]{x1D707}_{i}}{\hookrightarrow}\mathfrak{g}_{n}$
be the differentials of
$d\unicode[STIX]{x1D704}_{2}:\mathfrak{g}_{n-\unicode[STIX]{x1D707}_{i}}{\hookrightarrow}\mathfrak{g}_{n}$
be the differentials of
![]() $\unicode[STIX]{x1D704}_{1},\unicode[STIX]{x1D704}_{2}$
. These embeddings map the centralizers of
$\unicode[STIX]{x1D704}_{1},\unicode[STIX]{x1D704}_{2}$
. These embeddings map the centralizers of
![]() $S^{\prime }$
and
$S^{\prime }$
and
![]() $S^{\prime \prime }$
into the centralizer of
$S^{\prime \prime }$
into the centralizer of
![]() $S$
. Let
$S$
. Let
 $Y:=d\unicode[STIX]{x1D704}_{1}(\text{diag}(0,X))+d\unicode[STIX]{x1D704}_{2}(J_{\unicode[STIX]{x1D706}^{\prime }})\in \mathfrak{g}_{n}$
. Since
$Y:=d\unicode[STIX]{x1D704}_{1}(\text{diag}(0,X))+d\unicode[STIX]{x1D704}_{2}(J_{\unicode[STIX]{x1D706}^{\prime }})\in \mathfrak{g}_{n}$
. Since
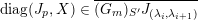 $\text{diag}(J_{p},X)\in \overline{(G_{m})_{S^{\prime }}J_{(\unicode[STIX]{x1D706}_{i},\unicode[STIX]{x1D706}_{i+1})}}$
, we have
$\text{diag}(J_{p},X)\in \overline{(G_{m})_{S^{\prime }}J_{(\unicode[STIX]{x1D706}_{i},\unicode[STIX]{x1D706}_{i+1})}}$
, we have
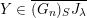 $Y\in \overline{(G_{n})_{S}J_{\unicode[STIX]{x1D706}}}$
. Since
$Y\in \overline{(G_{n})_{S}J_{\unicode[STIX]{x1D706}}}$
. Since
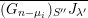 $\overline{(G_{n-\unicode[STIX]{x1D707}_{i}})_{S^{\prime \prime }}J_{\unicode[STIX]{x1D706}^{\prime }}}$
intersects
$\overline{(G_{n-\unicode[STIX]{x1D707}_{i}})_{S^{\prime \prime }}J_{\unicode[STIX]{x1D706}^{\prime }}}$
intersects
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D707}^{\prime }}$
,
${\mathcal{O}}_{\unicode[STIX]{x1D707}^{\prime }}$
,
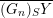 $\overline{(G_{n})_{S}Y}$
intersects
$\overline{(G_{n})_{S}Y}$
intersects
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D707}}$
and thus
${\mathcal{O}}_{\unicode[STIX]{x1D707}}$
and thus
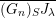 $\overline{(G_{n})_{S}J_{\unicode[STIX]{x1D706}}}$
intersects
$\overline{(G_{n})_{S}J_{\unicode[STIX]{x1D706}}}$
intersects
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D707}}$
.◻
${\mathcal{O}}_{\unicode[STIX]{x1D707}}$
.◻
4.3 Proof of Theorem E
In the archimedean case the theorem follows from Theorem 3.3.5 and Corollary 3.3.7. Thus, we assume here that
![]() $\mathbb{F}$
is non-archimedean. Let
$\mathbb{F}$
is non-archimedean. Let
![]() $\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
and let
$\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
and let
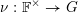 $\unicode[STIX]{x1D708}:\mathbb{F}^{\times }\rightarrow G$
be an algebraic group morphism (defined over
$\unicode[STIX]{x1D708}:\mathbb{F}^{\times }\rightarrow G$
be an algebraic group morphism (defined over
![]() $\mathbb{F}$
) such that
$\mathbb{F}$
) such that
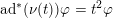 $\text{ad}^{\ast }(\unicode[STIX]{x1D708}(t))\unicode[STIX]{x1D711}=t^{2}\unicode[STIX]{x1D711}$
. Let
$\text{ad}^{\ast }(\unicode[STIX]{x1D708}(t))\unicode[STIX]{x1D711}=t^{2}\unicode[STIX]{x1D711}$
. Let
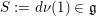 $S:=d\unicode[STIX]{x1D708}(1)\in \mathfrak{g}$
. Following [Reference Moeglin and WaldspurgerMW87] define
$S:=d\unicode[STIX]{x1D708}(1)\in \mathfrak{g}$
. Following [Reference Moeglin and WaldspurgerMW87] define
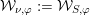 ${\mathcal{W}}_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D711}}:={\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
. For the following theorem see [Reference Moeglin and WaldspurgerMW87, Proposition I.11, Theorem I.16 and Corollary I.17] and [Reference VarmaVar14, Proposition 1 and Theorem 1].
${\mathcal{W}}_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D711}}:={\mathcal{W}}_{S,\unicode[STIX]{x1D711}}$
. For the following theorem see [Reference Moeglin and WaldspurgerMW87, Proposition I.11, Theorem I.16 and Corollary I.17] and [Reference VarmaVar14, Proposition 1 and Theorem 1].
Theorem 4.3.1. Let
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D708}$
be as above. Let
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D708}$
be as above. Let
 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
.
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G)$
.
-
(i) If
 ${\mathcal{W}}_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0$
, then
${\mathcal{W}}_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0$
, then
 $\unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})$
.
$\unicode[STIX]{x1D711}\in \operatorname{WF}(\unicode[STIX]{x1D70B})$
. -
(ii) If
 $\unicode[STIX]{x1D711}$
belongs to a maximal orbit
$\unicode[STIX]{x1D711}$
belongs to a maximal orbit
 ${\mathcal{O}}\in \operatorname{WFC}(\unicode[STIX]{x1D70B})$
, then
${\mathcal{O}}\in \operatorname{WFC}(\unicode[STIX]{x1D70B})$
, then
 ${\mathcal{W}}_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0$
and its dimension equals the coefficient of
${\mathcal{W}}_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0$
and its dimension equals the coefficient of
 ${\mathcal{O}}$
in
${\mathcal{O}}$
in
 $\operatorname{WFC}(\unicode[STIX]{x1D70B})$
.
$\operatorname{WFC}(\unicode[STIX]{x1D70B})$
.
Proof of Theorem E.
Let
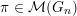 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
. Theorem 4.3.1 implies that if
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
. Theorem 4.3.1 implies that if
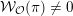 ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
, then
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
, then
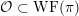 ${\mathcal{O}}\subset \operatorname{WF}(\unicode[STIX]{x1D70B})$
. Suppose now that
${\mathcal{O}}\subset \operatorname{WF}(\unicode[STIX]{x1D70B})$
. Suppose now that
 ${\mathcal{O}}\subset \operatorname{WF}(\unicode[STIX]{x1D70B})$
, i.e. there exists
${\mathcal{O}}\subset \operatorname{WF}(\unicode[STIX]{x1D70B})$
, i.e. there exists
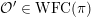 ${\mathcal{O}}^{\prime }\in \operatorname{WFC}(\unicode[STIX]{x1D70B})$
such that
${\mathcal{O}}^{\prime }\in \operatorname{WFC}(\unicode[STIX]{x1D70B})$
such that
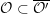 ${\mathcal{O}}\subset \overline{{\mathcal{O}}^{\prime }}$
. Let
${\mathcal{O}}\subset \overline{{\mathcal{O}}^{\prime }}$
. Let
![]() $\tilde{\unicode[STIX]{x1D711}}\in {\mathcal{O}}^{\prime }$
and
$\tilde{\unicode[STIX]{x1D711}}\in {\mathcal{O}}^{\prime }$
and
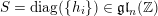 $S=\text{diag}(\{h_{i}\})\in \mathfrak{gl}_{n}(\mathbb{Z})$
be as in Theorem D. Define
$S=\text{diag}(\{h_{i}\})\in \mathfrak{gl}_{n}(\mathbb{Z})$
be as in Theorem D. Define
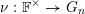 $\unicode[STIX]{x1D708}:\mathbb{F}^{\times }\rightarrow G_{n}$
by
$\unicode[STIX]{x1D708}:\mathbb{F}^{\times }\rightarrow G_{n}$
by
 $\unicode[STIX]{x1D708}(t):=\text{diag}(t^{h_{i}})$
. Then
$\unicode[STIX]{x1D708}(t):=\text{diag}(t^{h_{i}})$
. Then
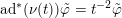 $\text{ad}^{\ast }(\unicode[STIX]{x1D708}(t))\tilde{\unicode[STIX]{x1D711}}=t^{-2}\tilde{\unicode[STIX]{x1D711}}$
and
$\text{ad}^{\ast }(\unicode[STIX]{x1D708}(t))\tilde{\unicode[STIX]{x1D711}}=t^{-2}\tilde{\unicode[STIX]{x1D711}}$
and
 ${\mathcal{W}}_{\unicode[STIX]{x1D708},\tilde{\unicode[STIX]{x1D711}}}={\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}$
. By Theorem 4.3.1
${\mathcal{W}}_{\unicode[STIX]{x1D708},\tilde{\unicode[STIX]{x1D711}}}={\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}$
. By Theorem 4.3.1
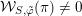 ${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})\neq 0$
and by Theorems A and D we have an epimorphism
${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})\neq 0$
and by Theorems A and D we have an epimorphism
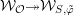 ${\mathcal{W}}_{{\mathcal{O}}}{\twoheadrightarrow}{\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}$
, hence
${\mathcal{W}}_{{\mathcal{O}}}{\twoheadrightarrow}{\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}$
, hence
 ${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})$
embeds into
${\mathcal{W}}_{S,\tilde{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70B})$
embeds into
![]() ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
, and thus
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$
, and thus
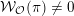 ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
.◻
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})\neq 0$
.◻
Remark 4.3.2. One can show that if
![]() $\unicode[STIX]{x1D707}$
is obtained from
$\unicode[STIX]{x1D707}$
is obtained from
![]() $\unicode[STIX]{x1D706}$
by taking some parts apart, or by replacing two parts of the same parity by two equal parts, then
$\unicode[STIX]{x1D706}$
by taking some parts apart, or by replacing two parts of the same parity by two equal parts, then
![]() ${\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D707}}}$
maps onto
${\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D707}}}$
maps onto
![]() ${\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}$
. This follows from Theorem A by taking
${\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}$
. This follows from Theorem A by taking
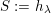 $S:=h_{\unicode[STIX]{x1D706}}$
,
$S:=h_{\unicode[STIX]{x1D706}}$
,
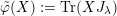 $\tilde{\unicode[STIX]{x1D711}}(X):=\text{Tr}(XJ_{\unicode[STIX]{x1D706}})$
and
$\tilde{\unicode[STIX]{x1D711}}(X):=\text{Tr}(XJ_{\unicode[STIX]{x1D706}})$
and
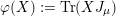 $\unicode[STIX]{x1D711}(X):=\text{Tr}(XJ_{\unicode[STIX]{x1D707}})$
. However, this does not extend to arbitrary
$\unicode[STIX]{x1D711}(X):=\text{Tr}(XJ_{\unicode[STIX]{x1D707}})$
. However, this does not extend to arbitrary
![]() $\unicode[STIX]{x1D707}\leqslant \unicode[STIX]{x1D706}$
. For example, if
$\unicode[STIX]{x1D707}\leqslant \unicode[STIX]{x1D706}$
. For example, if
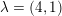 $\unicode[STIX]{x1D706}=(4,1)$
and
$\unicode[STIX]{x1D706}=(4,1)$
and
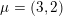 $\unicode[STIX]{x1D707}=(3,2)$
, then
$\unicode[STIX]{x1D707}=(3,2)$
, then
![]() $(\mathfrak{g}_{n}^{\ast })_{-2}^{h_{\unicode[STIX]{x1D706}}}$
does not intersect
$(\mathfrak{g}_{n}^{\ast })_{-2}^{h_{\unicode[STIX]{x1D706}}}$
does not intersect
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D707}}$
.
${\mathcal{O}}_{\unicode[STIX]{x1D707}}$
.
For the symplectic groups one can show that if
![]() $\unicode[STIX]{x1D707}$
is obtained from
$\unicode[STIX]{x1D707}$
is obtained from
![]() $\unicode[STIX]{x1D706}$
by replacing two parts of the same parity by two equal parts, then one can map the generalized Whittaker model corresponding to an orbit with partition
$\unicode[STIX]{x1D706}$
by replacing two parts of the same parity by two equal parts, then one can map the generalized Whittaker model corresponding to an orbit with partition
![]() $\unicode[STIX]{x1D707}$
onto the generalized Whittaker model corresponding to an orbit with partition
$\unicode[STIX]{x1D707}$
onto the generalized Whittaker model corresponding to an orbit with partition
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
4.4 Definition of derivatives and proof of Theorem F
The notion of derivative was first defined in [Reference Bernstein and ZelevinskyBZ77] for smooth representations of
![]() $G_{n}$
over non-archimedean fields and became a crucial tool in the study of this category. In [Reference Aizenbud, Gourevitch and SahiAGS15a] this construction was extended to the archimedean case.
$G_{n}$
over non-archimedean fields and became a crucial tool in the study of this category. In [Reference Aizenbud, Gourevitch and SahiAGS15a] this construction was extended to the archimedean case.
The definition of derivative is based on the ‘mirabolic’ subgroup
![]() $P_{n}$
of
$P_{n}$
of
![]() $G_{n}$
consisting of matrices with last row
$G_{n}$
consisting of matrices with last row
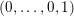 $(0,\ldots ,0,1)$
. The unipotent radical of this subgroup is an
$(0,\ldots ,0,1)$
. The unipotent radical of this subgroup is an
![]() $(n-1)$
-dimensional linear space that we denote
$(n-1)$
-dimensional linear space that we denote
![]() $V_{n}$
, and the reductive quotient is
$V_{n}$
, and the reductive quotient is
![]() $G_{n-1}$
. We have a natural isomorphism
$G_{n-1}$
. We have a natural isomorphism
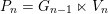 $P_{n}=G_{n-1}\ltimes V_{n}$
. The group
$P_{n}=G_{n-1}\ltimes V_{n}$
. The group
![]() $G_{n-1}$
has 2 orbits on
$G_{n-1}$
has 2 orbits on
![]() $V_{n}$
and, hence, also on the dual group
$V_{n}$
and, hence, also on the dual group
![]() $V_{n}^{\ast }$
: the zero and the non-zero orbit. The stabilizer in
$V_{n}^{\ast }$
: the zero and the non-zero orbit. The stabilizer in
![]() $G_{n-1}$
of a non-trivial character of
$G_{n-1}$
of a non-trivial character of
![]() $V_{n}$
is isomorphic to
$V_{n}$
is isomorphic to
![]() $P_{n-1}$
.
$P_{n-1}$
.
Let
![]() $\unicode[STIX]{x1D713}_{n}$
be the standard non-trivial unitary character of
$\unicode[STIX]{x1D713}_{n}$
be the standard non-trivial unitary character of
![]() $V_{n}$
, given by
$V_{n}$
, given by
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{n}(x_{1},\ldots ,x_{n-1}):=\unicode[STIX]{x1D712}(x_{n-1}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{n}(x_{1},\ldots ,x_{n-1}):=\unicode[STIX]{x1D712}(x_{n-1}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D712}$
is the fixed additive character of
$\unicode[STIX]{x1D712}$
is the fixed additive character of
![]() $\mathbb{F}$
, as in (7). We will also denote by
$\mathbb{F}$
, as in (7). We will also denote by
![]() $\unicode[STIX]{x1D713}_{n}$
the corresponding character of the Lie algebra
$\unicode[STIX]{x1D713}_{n}$
the corresponding character of the Lie algebra
![]() $\mathfrak{v}_{n}$
. For all
$\mathfrak{v}_{n}$
. For all
![]() $n$
and for all smooth representations
$n$
and for all smooth representations
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $P_{n}$
, we define
$P_{n}$
, we define
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(V_{n},\unicode[STIX]{x1D713}_{n}):=\text{Span}\{\unicode[STIX]{x1D70B}(a)v-\unicode[STIX]{x1D713}_{n}(a)v\,:\,v\in \unicode[STIX]{x1D70B},\,a\in V_{n}\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(V_{n},\unicode[STIX]{x1D713}_{n}):=\text{Span}\{\unicode[STIX]{x1D70B}(a)v-\unicode[STIX]{x1D713}_{n}(a)v\,:\,v\in \unicode[STIX]{x1D70B},\,a\in V_{n}\},\end{eqnarray}$$
and we put
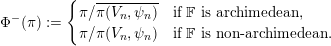 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{-}(\unicode[STIX]{x1D70B}):=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D70B}/\overline{\unicode[STIX]{x1D70B}(V_{n},\unicode[STIX]{x1D713}_{n})}\quad & \text{if }\mathbb{F}\text{ is archimedean},\\ \unicode[STIX]{x1D70B}/\unicode[STIX]{x1D70B}(V_{n},\unicode[STIX]{x1D713}_{n})\quad & \text{if }\mathbb{F}\text{ is non-archimedean}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{-}(\unicode[STIX]{x1D70B}):=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D70B}/\overline{\unicode[STIX]{x1D70B}(V_{n},\unicode[STIX]{x1D713}_{n})}\quad & \text{if }\mathbb{F}\text{ is archimedean},\\ \unicode[STIX]{x1D70B}/\unicode[STIX]{x1D70B}(V_{n},\unicode[STIX]{x1D713}_{n})\quad & \text{if }\mathbb{F}\text{ is non-archimedean}.\end{array}\right.\end{eqnarray}$$
If
![]() $\mathbb{F}$
is non-archimedean, our definition of
$\mathbb{F}$
is non-archimedean, our definition of
![]() $\unicode[STIX]{x1D6F7}^{-}$
coincides with that in [Reference Bernstein and ZelevinskyBZ76, § 5.11]. It differs from the definition in [Reference Bernstein and ZelevinskyBZ77] by the twist by the character
$\unicode[STIX]{x1D6F7}^{-}$
coincides with that in [Reference Bernstein and ZelevinskyBZ76, § 5.11]. It differs from the definition in [Reference Bernstein and ZelevinskyBZ77] by the twist by the character
![]() $|\det |^{1/2}$
.
$|\det |^{1/2}$
.
For a smooth representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $G_{n}$
we define a representation
$G_{n}$
we define a representation
![]() $E^{k}(\unicode[STIX]{x1D70B})$
of
$E^{k}(\unicode[STIX]{x1D70B})$
of
![]() $G_{n-k}$
by
$G_{n-k}$
by
 $$\begin{eqnarray}E^{k}(\unicode[STIX]{x1D70B}):=((\unicode[STIX]{x1D6F7}^{-})^{k-1}(\unicode[STIX]{x1D70B}|_{P_{n}}))|_{G_{n}}.\end{eqnarray}$$
$$\begin{eqnarray}E^{k}(\unicode[STIX]{x1D70B}):=((\unicode[STIX]{x1D6F7}^{-})^{k-1}(\unicode[STIX]{x1D70B}|_{P_{n}}))|_{G_{n}}.\end{eqnarray}$$
We call it the
![]() $k$
th pre-derivative of
$k$
th pre-derivative of
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
Define also a functor
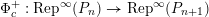 $\unicode[STIX]{x1D6F7}_{c}^{+}:\text{Rep}^{\infty }(P_{n})\rightarrow \text{Rep}^{\infty }(P_{n+1})$
by
$\unicode[STIX]{x1D6F7}_{c}^{+}:\text{Rep}^{\infty }(P_{n})\rightarrow \text{Rep}^{\infty }(P_{n+1})$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{c}^{+}(\unicode[STIX]{x1D70B})=\text{ind}_{P_{n}\ltimes V_{n+1}}^{P_{n+1}}(\unicode[STIX]{x1D70B}\boxtimes \unicode[STIX]{x1D713}_{n+1}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{c}^{+}(\unicode[STIX]{x1D70B})=\text{ind}_{P_{n}\ltimes V_{n+1}}^{P_{n+1}}(\unicode[STIX]{x1D70B}\boxtimes \unicode[STIX]{x1D713}_{n+1}),\end{eqnarray}$$
where
![]() $\text{Rep}^{\infty }$
denotes the category of smooth representations as in Definition 2.3.1, and
$\text{Rep}^{\infty }$
denotes the category of smooth representations as in Definition 2.3.1, and
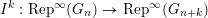 $I^{k}:\text{Rep}^{\infty }(G_{n})\rightarrow \text{Rep}^{\infty }(G_{n+k})$
by
$I^{k}:\text{Rep}^{\infty }(G_{n})\rightarrow \text{Rep}^{\infty }(G_{n+k})$
by
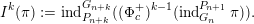 $$\begin{eqnarray}I^{k}(\unicode[STIX]{x1D70B}):=\text{ind}_{P_{n+k}}^{G_{n+k}}((\unicode[STIX]{x1D6F7}_{c}^{+})^{k-1}(\text{ind}_{G_{n}}^{P_{n+1}}\,\unicode[STIX]{x1D70B})).\end{eqnarray}$$
$$\begin{eqnarray}I^{k}(\unicode[STIX]{x1D70B}):=\text{ind}_{P_{n+k}}^{G_{n+k}}((\unicode[STIX]{x1D6F7}_{c}^{+})^{k-1}(\text{ind}_{G_{n}}^{P_{n+1}}\,\unicode[STIX]{x1D70B})).\end{eqnarray}$$
Lemma 4.4.1. Let
![]() $\unicode[STIX]{x1D706}$
be a partition of
$\unicode[STIX]{x1D706}$
be a partition of
![]() $n$
and let
$n$
and let
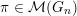 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
. Then
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
. Then
 $$\begin{eqnarray}\text{Hom}_{G_{n}} (I^{\unicode[STIX]{x1D706}_{1}}(I^{\unicode[STIX]{x1D706}_{2}}(\ldots I^{\unicode[STIX]{x1D706}_{k}}(\mathbb{C})\ldots ),\widetilde{\unicode[STIX]{x1D70B}})=(E^{\unicode[STIX]{x1D706}_{k}}(\ldots (E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})\ldots )))^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{G_{n}} (I^{\unicode[STIX]{x1D706}_{1}}(I^{\unicode[STIX]{x1D706}_{2}}(\ldots I^{\unicode[STIX]{x1D706}_{k}}(\mathbb{C})\ldots ),\widetilde{\unicode[STIX]{x1D70B}})=(E^{\unicode[STIX]{x1D706}_{k}}(\ldots (E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})\ldots )))^{\ast }.\end{eqnarray}$$
The proof of this lemma is analogous to the proof of Lemma 2.5.2.
If
![]() $\mathbb{F}$
is archimedean, then the space
$\mathbb{F}$
is archimedean, then the space
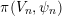 $\unicode[STIX]{x1D70B}(V_{n},\unicode[STIX]{x1D713}_{n})$
has the same closure as the space
$\unicode[STIX]{x1D70B}(V_{n},\unicode[STIX]{x1D713}_{n})$
has the same closure as the space
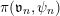 $\unicode[STIX]{x1D70B}(\mathfrak{v}_{n},\unicode[STIX]{x1D713}_{n})$
defined analogously using the Lie algebra action, since both closures equal to the joint kernel of all
$\unicode[STIX]{x1D70B}(\mathfrak{v}_{n},\unicode[STIX]{x1D713}_{n})$
defined analogously using the Lie algebra action, since both closures equal to the joint kernel of all
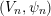 $(V_{n},\unicode[STIX]{x1D713}_{n})$
-equivariant continuous functionals on
$(V_{n},\unicode[STIX]{x1D713}_{n})$
-equivariant continuous functionals on
![]() $\unicode[STIX]{x1D70B}$
. It is shown in [Reference Aizenbud, Gourevitch and SahiAGS15b] that if
$\unicode[STIX]{x1D70B}$
. It is shown in [Reference Aizenbud, Gourevitch and SahiAGS15b] that if
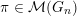 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
, then
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
, then
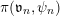 $\unicode[STIX]{x1D70B}(\mathfrak{v}_{n},\unicode[STIX]{x1D713}_{n})$
is closed. Moreover, it is shown that for any
$\unicode[STIX]{x1D70B}(\mathfrak{v}_{n},\unicode[STIX]{x1D713}_{n})$
is closed. Moreover, it is shown that for any
![]() $i$
, the space
$i$
, the space
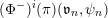 $(\unicode[STIX]{x1D6F7}^{-})^{i}(\unicode[STIX]{x1D70B})(\mathfrak{v}_{n},\unicode[STIX]{x1D713}_{n})$
is closed in this case. Thus, for
$(\unicode[STIX]{x1D6F7}^{-})^{i}(\unicode[STIX]{x1D70B})(\mathfrak{v}_{n},\unicode[STIX]{x1D713}_{n})$
is closed in this case. Thus, for
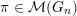 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
our definition of
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
our definition of
![]() $E^{k}$
coincides with the functor
$E^{k}$
coincides with the functor
![]() $\tilde{E}^{k}$
used in [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b]. It differs from the functor
$\tilde{E}^{k}$
used in [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b]. It differs from the functor
![]() $E^{k}$
used in [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b] by the twist by the character
$E^{k}$
used in [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b] by the twist by the character
 $|\det |^{(k-1)/2}$
. Note though that for non-admissible smooth
$|\det |^{(k-1)/2}$
. Note though that for non-admissible smooth
![]() $\unicode[STIX]{x1D70B}$
our definition of
$\unicode[STIX]{x1D70B}$
our definition of
![]() $E^{k}$
might differ from the functor
$E^{k}$
might differ from the functor
![]() $\tilde{E}^{k}$
used in [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b].
$\tilde{E}^{k}$
used in [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b].
Let us now start proving Theorem F. Let
![]() $\unicode[STIX]{x1D706}$
be a partition of
$\unicode[STIX]{x1D706}$
be a partition of
![]() $n$
and
$n$
and
![]() $\unicode[STIX]{x1D702}$
be the inverse reordering of
$\unicode[STIX]{x1D702}$
be the inverse reordering of
![]() $\unicode[STIX]{x1D706}$
. Let
$\unicode[STIX]{x1D706}$
. Let
![]() $f:=J_{\unicode[STIX]{x1D702}}$
,
$f:=J_{\unicode[STIX]{x1D702}}$
,
![]() $h:=h_{\unicode[STIX]{x1D702}}$
and let
$h:=h_{\unicode[STIX]{x1D702}}$
and let
![]() $e\in \mathfrak{g}_{n}$
be the unique element such that
$e\in \mathfrak{g}_{n}$
be the unique element such that
![]() $(f,h,e)$
is an
$(f,h,e)$
is an
![]() $\mathfrak{sl}_{2}$
triple. We will prove Theorem F by induction on
$\mathfrak{sl}_{2}$
triple. We will prove Theorem F by induction on
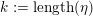 $k:=\text{length}(\unicode[STIX]{x1D702})$
. Let
$k:=\text{length}(\unicode[STIX]{x1D702})$
. Let
![]() $Z$
be a diagonal matrix with first
$Z$
be a diagonal matrix with first
![]() $n-\unicode[STIX]{x1D702}_{k}$
entries equal to zero, and last
$n-\unicode[STIX]{x1D702}_{k}$
entries equal to zero, and last
![]() $\unicode[STIX]{x1D702}_{k}$
entries equal to
$\unicode[STIX]{x1D702}_{k}$
entries equal to
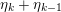 $\unicode[STIX]{x1D702}_{k}+\unicode[STIX]{x1D702}_{k-1}$
. Define
$\unicode[STIX]{x1D702}_{k}+\unicode[STIX]{x1D702}_{k-1}$
. Define
![]() $\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
by
$\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
by
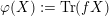 $\unicode[STIX]{x1D711}(X):=\text{Tr}(fX)$
and let
$\unicode[STIX]{x1D711}(X):=\text{Tr}(fX)$
and let
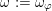 $\unicode[STIX]{x1D714}:=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}$
. For
$\unicode[STIX]{x1D714}:=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}$
. For
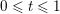 $0\leqslant t\leqslant 1$
let
$0\leqslant t\leqslant 1$
let
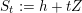 $S_{t}:=h+tZ$
and define
$S_{t}:=h+tZ$
and define
![]() $\mathfrak{u}_{t},\mathfrak{l}_{t}$
and
$\mathfrak{u}_{t},\mathfrak{l}_{t}$
and
![]() $\mathfrak{r}_{t}$
as in formulas (14), (15) in § 3.2 (note though that our
$\mathfrak{r}_{t}$
as in formulas (14), (15) in § 3.2 (note though that our
![]() $\mathfrak{l}_{t}^{\prime },\mathfrak{r}_{t}^{\prime }$
differ from those in formula (16)). Let
$\mathfrak{l}_{t}^{\prime },\mathfrak{r}_{t}^{\prime }$
differ from those in formula (16)). Let
![]() $\mathfrak{a}$
denote the stabilizer of the standard basis vector
$\mathfrak{a}$
denote the stabilizer of the standard basis vector
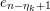 $e_{n-\unicode[STIX]{x1D702}_{k}+1}$
and define
$e_{n-\unicode[STIX]{x1D702}_{k}+1}$
and define
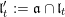 $\mathfrak{l}_{t}^{\prime }:=\mathfrak{a}\cap \mathfrak{l}_{t}$
,
$\mathfrak{l}_{t}^{\prime }:=\mathfrak{a}\cap \mathfrak{l}_{t}$
,
 $\mathfrak{r}_{t}^{\prime }:=\mathfrak{a}\cap \mathfrak{r}_{t}$
.
$\mathfrak{r}_{t}^{\prime }:=\mathfrak{a}\cap \mathfrak{r}_{t}$
.
Lemma 4.4.2. We have:
-
(i)
 $\mathfrak{l}_{t}^{\prime }$
and
$\mathfrak{l}_{t}^{\prime }$
and
 $\mathfrak{r}_{t}^{\prime }$
are subalgebras of
$\mathfrak{r}_{t}^{\prime }$
are subalgebras of
 $\mathfrak{u}_{t}$
and
$\mathfrak{u}_{t}$
and
 $[\mathfrak{l}_{t}^{\prime },\mathfrak{r}_{t}^{\prime }]\subset \mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
;
$[\mathfrak{l}_{t}^{\prime },\mathfrak{r}_{t}^{\prime }]\subset \mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
; -
(ii)
 $\mathfrak{u}_{0}\subset \mathfrak{a}$
and thus
$\mathfrak{u}_{0}\subset \mathfrak{a}$
and thus
 $\mathfrak{l}_{0}=\mathfrak{l}_{0}^{\prime }$
.
$\mathfrak{l}_{0}=\mathfrak{l}_{0}^{\prime }$
.
Proof. Part (i) follows from Lemma 3.2.7(i) and the fact that
![]() $\mathfrak{a}$
is a subalgebra of
$\mathfrak{a}$
is a subalgebra of
![]() $\mathfrak{g}$
.
$\mathfrak{g}$
.
For part (ii) note that the
![]() $h$
-weight of
$h$
-weight of
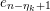 $e_{n-\unicode[STIX]{x1D702}_{k}+1}$
is the maximal weight inside the standard representation, and thus any element of
$e_{n-\unicode[STIX]{x1D702}_{k}+1}$
is the maximal weight inside the standard representation, and thus any element of
![]() $\mathfrak{u}_{0}$
annihilates it.◻
$\mathfrak{u}_{0}$
annihilates it.◻
The next lemma follows from the structure of the lowest-weight vectors in a tensor product of irreducible representations of
![]() $\mathfrak{sl}_{2}$
.
$\mathfrak{sl}_{2}$
.
Lemma 4.4.3. Let
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70F}$
be two irreducible representations of an
$\unicode[STIX]{x1D70F}$
be two irreducible representations of an
![]() $\mathfrak{sl}_{2}$
-triple
$\mathfrak{sl}_{2}$
-triple
![]() $(f,h,e)$
with
$(f,h,e)$
with
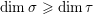 $\dim \unicode[STIX]{x1D70E}\geqslant \dim \unicode[STIX]{x1D70F}$
. Let
$\dim \unicode[STIX]{x1D70E}\geqslant \dim \unicode[STIX]{x1D70F}$
. Let
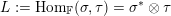 $L:=\text{Hom}_{\mathbb{F}}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D70E}^{\ast }\otimes \unicode[STIX]{x1D70F}$
. Let
$L:=\text{Hom}_{\mathbb{F}}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D70E}^{\ast }\otimes \unicode[STIX]{x1D70F}$
. Let
![]() $L^{0}$
denote the annihilator in
$L^{0}$
denote the annihilator in
![]() $L$
of the highest-weight vector in
$L$
of the highest-weight vector in
![]() $\unicode[STIX]{x1D70E}$
, and
$\unicode[STIX]{x1D70E}$
, and
![]() $L^{f}$
denote the space spanned by all the lowest-weight vectors in
$L^{f}$
denote the space spanned by all the lowest-weight vectors in
![]() $L$
. Then
$L$
. Then
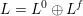 $L=L^{0}\oplus L^{f}$
.
$L=L^{0}\oplus L^{f}$
.
Lemma 4.4.4. We have
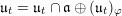 $\mathfrak{u}_{t}=\mathfrak{u}_{t}\cap \mathfrak{a}\oplus (\mathfrak{u}_{t})_{\unicode[STIX]{x1D711}}$
.
$\mathfrak{u}_{t}=\mathfrak{u}_{t}\cap \mathfrak{a}\oplus (\mathfrak{u}_{t})_{\unicode[STIX]{x1D711}}$
.
Proof. First decompose
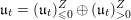 $\mathfrak{u}_{t}=(\mathfrak{u}_{t})_{{\leqslant}0}^{Z}\oplus (\mathfrak{u}_{t})_{{>}0}^{Z}$
and note that
$\mathfrak{u}_{t}=(\mathfrak{u}_{t})_{{\leqslant}0}^{Z}\oplus (\mathfrak{u}_{t})_{{>}0}^{Z}$
and note that
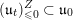 $(\mathfrak{u}_{t})_{{\leqslant}0}^{Z}\subset \mathfrak{u}_{0}$
and thus
$(\mathfrak{u}_{t})_{{\leqslant}0}^{Z}\subset \mathfrak{u}_{0}$
and thus
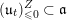 $(\mathfrak{u}_{t})_{{\leqslant}0}^{Z}\subset \mathfrak{a}$
and
$(\mathfrak{u}_{t})_{{\leqslant}0}^{Z}\subset \mathfrak{a}$
and
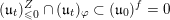 $(\mathfrak{u}_{t})_{{\leqslant}0}^{Z}\cap (\mathfrak{u}_{t})_{\unicode[STIX]{x1D711}}\subset (\mathfrak{u}_{0})^{f}=0$
. Now let
$(\mathfrak{u}_{t})_{{\leqslant}0}^{Z}\cap (\mathfrak{u}_{t})_{\unicode[STIX]{x1D711}}\subset (\mathfrak{u}_{0})^{f}=0$
. Now let
![]() $V$
denote the standard representation of
$V$
denote the standard representation of
![]() $\mathfrak{g}_{n}$
and consider the decomposition
$\mathfrak{g}_{n}$
and consider the decomposition
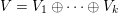 $V=V_{1}\oplus \ldots \oplus V_{k}$
, where each
$V=V_{1}\oplus \ldots \oplus V_{k}$
, where each
![]() $V_{i}$
is the subspace spanned by the basic vectors with indices from
$V_{i}$
is the subspace spanned by the basic vectors with indices from
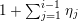 $1+\sum _{j=1}^{i-1}\unicode[STIX]{x1D702}_{j}$
to
$1+\sum _{j=1}^{i-1}\unicode[STIX]{x1D702}_{j}$
to
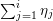 $\sum _{j=1}^{i}\unicode[STIX]{x1D702}_{j}$
. Note that
$\sum _{j=1}^{i}\unicode[STIX]{x1D702}_{j}$
. Note that
![]() $V_{i}$
is an irreducible representation of the
$V_{i}$
is an irreducible representation of the
![]() $\mathfrak{sl}_{2}$
triple
$\mathfrak{sl}_{2}$
triple
![]() $(f,h,e)$
of dimension
$(f,h,e)$
of dimension
![]() $\unicode[STIX]{x1D702}_{i}$
. Then
$\unicode[STIX]{x1D702}_{i}$
. Then
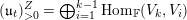 $(\mathfrak{u}_{t})_{{>}0}^{Z}=\bigoplus _{i=1}^{k-1}\text{Hom}_{\mathbb{F}}(V_{k},V_{i})$
. By Lemma 4.4.3 we have
$(\mathfrak{u}_{t})_{{>}0}^{Z}=\bigoplus _{i=1}^{k-1}\text{Hom}_{\mathbb{F}}(V_{k},V_{i})$
. By Lemma 4.4.3 we have
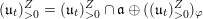 $(\mathfrak{u}_{t})_{{>}0}^{Z}=(\mathfrak{u}_{t})_{{>}0}^{Z}\cap \mathfrak{a}\oplus ((\mathfrak{u}_{t})_{{>}0}^{Z})_{\unicode[STIX]{x1D711}}$
.◻
$(\mathfrak{u}_{t})_{{>}0}^{Z}=(\mathfrak{u}_{t})_{{>}0}^{Z}\cap \mathfrak{a}\oplus ((\mathfrak{u}_{t})_{{>}0}^{Z})_{\unicode[STIX]{x1D711}}$
.◻
Corollary 4.4.5. The radical of the restriction
![]() $\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}^{\prime }+\mathfrak{r}_{t}^{\prime }}$
is
$\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}^{\prime }+\mathfrak{r}_{t}^{\prime }}$
is
![]() $\mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
.
$\mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
.
Proof. By Lemma 3.2.7(ii) we have
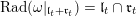 $\text{Rad}(\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}+\mathfrak{r}_{t}})=\mathfrak{l}_{t}\cap \mathfrak{r}_{t}$
and thus
$\text{Rad}(\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}+\mathfrak{r}_{t}})=\mathfrak{l}_{t}\cap \mathfrak{r}_{t}$
and thus
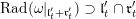 $\text{Rad}(\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}^{\prime }+\mathfrak{r}_{t}^{\prime }})\supset \mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
. Now,
$\text{Rad}(\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}^{\prime }+\mathfrak{r}_{t}^{\prime }})\supset \mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
. Now,
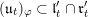 $(\mathfrak{u}_{t})_{\unicode[STIX]{x1D711}}\subset \mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
and by Lemma 4.4.4 the image of
$(\mathfrak{u}_{t})_{\unicode[STIX]{x1D711}}\subset \mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
and by Lemma 4.4.4 the image of
![]() $\mathfrak{l}_{t}^{\prime }$
in
$\mathfrak{l}_{t}^{\prime }$
in
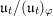 $\mathfrak{u}_{t}/(\mathfrak{u}_{t})_{\unicode[STIX]{x1D711}}$
coincides with the image of
$\mathfrak{u}_{t}/(\mathfrak{u}_{t})_{\unicode[STIX]{x1D711}}$
coincides with the image of
![]() $\mathfrak{l}_{t}$
and the image of
$\mathfrak{l}_{t}$
and the image of
![]() $\mathfrak{r}_{t}^{\prime }$
in
$\mathfrak{r}_{t}^{\prime }$
in
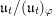 $\mathfrak{u}_{t}/(\mathfrak{u}_{t})_{\unicode[STIX]{x1D711}}$
coincides with the image of
$\mathfrak{u}_{t}/(\mathfrak{u}_{t})_{\unicode[STIX]{x1D711}}$
coincides with the image of
![]() $\mathfrak{r}_{t}$
. Thus,
$\mathfrak{r}_{t}$
. Thus,
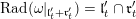 $\text{Rad}(\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}^{\prime }+\mathfrak{r}_{t}^{\prime }})=\mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
.◻
$\text{Rad}(\unicode[STIX]{x1D714}|_{\mathfrak{l}_{t}^{\prime }+\mathfrak{r}_{t}^{\prime }})=\mathfrak{l}_{t}^{\prime }\cap \mathfrak{r}_{t}^{\prime }$
.◻
Recall Definition 3.2.5 of regular and critical numbers.
Lemma 4.4.6. For
![]() $s<t$
with no critical numbers in the open interval
$s<t$
with no critical numbers in the open interval
![]() $(s,t)$
we have
$(s,t)$
we have
![]() $\mathfrak{r}_{s}^{\prime }=\mathfrak{l}_{t}^{\prime }$
.
$\mathfrak{r}_{s}^{\prime }=\mathfrak{l}_{t}^{\prime }$
.
Proof. By Lemma 3.2.7(iii) we have
![]() $\mathfrak{r}_{s}\subset \mathfrak{l}_{t}$
and thus
$\mathfrak{r}_{s}\subset \mathfrak{l}_{t}$
and thus
![]() $\mathfrak{r}_{s}^{\prime }\subset \mathfrak{l}_{t}^{\prime }$
. For the inverse inclusion note that
$\mathfrak{r}_{s}^{\prime }\subset \mathfrak{l}_{t}^{\prime }$
. For the inverse inclusion note that
 $$\begin{eqnarray}\mathfrak{l}_{t}^{\prime }=\mathfrak{m}\oplus (\mathfrak{v}_{t})_{{\leqslant}0}^{Z}\oplus (\mathfrak{v}_{t})_{{>}0}^{Z}\oplus (\mathfrak{w}_{t})_{{<}0}^{Z}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{l}_{t}^{\prime }=\mathfrak{m}\oplus (\mathfrak{v}_{t})_{{\leqslant}0}^{Z}\oplus (\mathfrak{v}_{t})_{{>}0}^{Z}\oplus (\mathfrak{w}_{t})_{{<}0}^{Z}.\end{eqnarray}$$
We have
![]() $\mathfrak{m}\subset \mathfrak{r}_{s}^{\prime }$
;
$\mathfrak{m}\subset \mathfrak{r}_{s}^{\prime }$
;
 $(\mathfrak{v}_{t})_{{\leqslant}0}^{Z}\oplus (\mathfrak{w}_{t})_{{<}0}^{Z}\subset \mathfrak{v}_{s}\subset \mathfrak{r}_{s}^{\prime }$
. Since there are no critical elements in
$(\mathfrak{v}_{t})_{{\leqslant}0}^{Z}\oplus (\mathfrak{w}_{t})_{{<}0}^{Z}\subset \mathfrak{v}_{s}\subset \mathfrak{r}_{s}^{\prime }$
. Since there are no critical elements in
![]() $(s,t)$
we also have
$(s,t)$
we also have
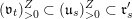 $(\mathfrak{v}_{t})_{{>}0}^{Z}\subset (\mathfrak{u}_{s})_{{>}0}^{Z}\subset \mathfrak{r}_{s}^{\prime }$
.◻
$(\mathfrak{v}_{t})_{{>}0}^{Z}\subset (\mathfrak{u}_{s})_{{>}0}^{Z}\subset \mathfrak{r}_{s}^{\prime }$
.◻
Proof of Theorem F.
Corollary 4.4.5 and Lemmas 4.4.6 and 3.2.1 imply
 $$\begin{eqnarray}{\mathcal{W}}_{h,\unicode[STIX]{x1D711}}^{G_{n}}\simeq \text{ind}_{\text{Exp}(\mathfrak{l}_{0})}^{G_{n}}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{1}^{\prime })}^{G_{n}}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{h,\unicode[STIX]{x1D711}}^{G_{n}}\simeq \text{ind}_{\text{Exp}(\mathfrak{l}_{0})}^{G_{n}}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})\simeq \text{ind}_{\text{Exp}(\mathfrak{r}_{1}^{\prime })}^{G_{n}}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}).\end{eqnarray}$$
Let
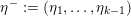 $\unicode[STIX]{x1D702}^{-}:=(\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{k-1})$
and consider the corresponding elements
$\unicode[STIX]{x1D702}^{-}:=(\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{k-1})$
and consider the corresponding elements
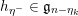 $h_{\unicode[STIX]{x1D702}^{-}}\in \mathfrak{g}_{n-\unicode[STIX]{x1D702}_{k}}$
and
$h_{\unicode[STIX]{x1D702}^{-}}\in \mathfrak{g}_{n-\unicode[STIX]{x1D702}_{k}}$
and
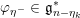 $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D702}^{-}}\in \mathfrak{g}_{n-\unicode[STIX]{x1D702}_{k}}^{\ast }$
. Note that
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D702}^{-}}\in \mathfrak{g}_{n-\unicode[STIX]{x1D702}_{k}}^{\ast }$
. Note that
 $$\begin{eqnarray}\text{ind}_{\text{Exp}(\mathfrak{r}_{1}^{\prime })}^{G_{n}}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})\simeq I^{\unicode[STIX]{x1D702}_{k}}({\mathcal{W}}_{h_{\unicode[STIX]{x1D702}^{-}},\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D702}^{-}}}^{G_{n-\unicode[STIX]{x1D702}_{k}}})=I^{\unicode[STIX]{x1D702}_{k}}({\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D702}}}^{G_{n-\unicode[STIX]{x1D702}_{k}}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{ind}_{\text{Exp}(\mathfrak{r}_{1}^{\prime })}^{G_{n}}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}})\simeq I^{\unicode[STIX]{x1D702}_{k}}({\mathcal{W}}_{h_{\unicode[STIX]{x1D702}^{-}},\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D702}^{-}}}^{G_{n-\unicode[STIX]{x1D702}_{k}}})=I^{\unicode[STIX]{x1D702}_{k}}({\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D702}}}^{G_{n-\unicode[STIX]{x1D702}_{k}}}).\end{eqnarray}$$
The isomorphism (4) now follows by induction on
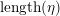 $\text{length}(\unicode[STIX]{x1D702})$
. The isomorphism (5) follows from (4) using Lemma 4.4.1.◻
$\text{length}(\unicode[STIX]{x1D702})$
. The isomorphism (5) follows from (4) using Lemma 4.4.1.◻
4.5 Proof of Corollary G
For non-archimedean
![]() $\mathbb{F}$
, exactness is well-known, the rest of part (i) follows from Theorem 4.3.1, and part (ii) follows from [Reference Moeglin and WaldspurgerMW87, § II.2]. Thus, we assume that
$\mathbb{F}$
, exactness is well-known, the rest of part (i) follows from Theorem 4.3.1, and part (ii) follows from [Reference Moeglin and WaldspurgerMW87, § II.2]. Thus, we assume that
![]() $\mathbb{F}$
is archimedean.
$\mathbb{F}$
is archimedean.
4.5.1 Preliminaries on pre-derivatives
The highest non-zero pre-derivative of
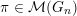 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
plays a special role. It has better properties than the other derivatives. In particular it is also admissible. The index of the highest non-zero pre-derivative is called the depth of
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
plays a special role. It has better properties than the other derivatives. In particular it is also admissible. The index of the highest non-zero pre-derivative is called the depth of
![]() $\unicode[STIX]{x1D70B}$
. As shown in [Reference Gourevitch and SahiGS13, Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Gourevitch and SahiGS15] the depth also equals the maximum among the first parts of the partitions in the orbits in
$\unicode[STIX]{x1D70B}$
. As shown in [Reference Gourevitch and SahiGS13, Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Gourevitch and SahiGS15] the depth also equals the maximum among the first parts of the partitions in the orbits in
![]() $\operatorname{WF}(\unicode[STIX]{x1D70B})$
. The following theorem summarizes the main results of [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b].
$\operatorname{WF}(\unicode[STIX]{x1D70B})$
. The following theorem summarizes the main results of [Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b].
Theorem 4.5.1. Let
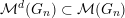 ${\mathcal{M}}^{d}(G_{n})\subset {\mathcal{M}}(G_{n})$
denote the subcategory of representations of depth
${\mathcal{M}}^{d}(G_{n})\subset {\mathcal{M}}(G_{n})$
denote the subcategory of representations of depth
![]() ${\leqslant}d$
.
${\leqslant}d$
.
-
(i) The functor
 $E^{k}:{\mathcal{M}}(G_{n})\rightarrow \text{Rep}^{\infty }(P_{n-k+1})$
is exact for any
$E^{k}:{\mathcal{M}}(G_{n})\rightarrow \text{Rep}^{\infty }(P_{n-k+1})$
is exact for any
 $1\leqslant k\leqslant n$
.
$1\leqslant k\leqslant n$
. -
(ii) The functor
 $E^{d}$
maps
$E^{d}$
maps
 ${\mathcal{M}}^{d}(G_{n})$
into
${\mathcal{M}}^{d}(G_{n})$
into
 ${\mathcal{M}}(G_{n-d})$
.
${\mathcal{M}}(G_{n-d})$
. -
(iii) Let
 $n=n_{1}+\cdots +n_{d}$
and let
$n=n_{1}+\cdots +n_{d}$
and let
 $\unicode[STIX]{x1D712}_{i}$
be characters of
$\unicode[STIX]{x1D712}_{i}$
be characters of
 $G_{n_{i}}$
. Let
$G_{n_{i}}$
. Let
 $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D712}_{1}\times \cdots \times \unicode[STIX]{x1D712}_{d}\in {\mathcal{M}}^{d}(G_{n})$
denote the corresponding monomial representation. Then
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D712}_{1}\times \cdots \times \unicode[STIX]{x1D712}_{d}\in {\mathcal{M}}^{d}(G_{n})$
denote the corresponding monomial representation. Then  $$\begin{eqnarray}E^{d}(\unicode[STIX]{x1D70B})\cong ((\unicode[STIX]{x1D712}_{1})|_{G_{n_{1}-1}}\times \cdots \times (\unicode[STIX]{x1D712}_{d})|_{G_{n_{d}-1}}).\end{eqnarray}$$
$$\begin{eqnarray}E^{d}(\unicode[STIX]{x1D70B})\cong ((\unicode[STIX]{x1D712}_{1})|_{G_{n_{1}-1}}\times \cdots \times (\unicode[STIX]{x1D712}_{d})|_{G_{n_{d}-1}}).\end{eqnarray}$$
-
(iv) If
 $\unicode[STIX]{x1D70F}$
is an irreducible unitary representation of
$\unicode[STIX]{x1D70F}$
is an irreducible unitary representation of
 $G_{n}$
and
$G_{n}$
and
 $\unicode[STIX]{x1D70F}^{\infty }$
has depth
$\unicode[STIX]{x1D70F}^{\infty }$
has depth
 $d$
, then
$d$
, then
 $E^{d}(\unicode[STIX]{x1D70F}^{\infty })\cong (A\unicode[STIX]{x1D70F})^{\infty }$
, where
$E^{d}(\unicode[STIX]{x1D70F}^{\infty })\cong (A\unicode[STIX]{x1D70F})^{\infty }$
, where
 $A\unicode[STIX]{x1D70F}$
denotes the (irreducible, unitary) adduced representation defined in [Reference SahiSah89] (cf. [Reference BaruchBar03]).
$A\unicode[STIX]{x1D70F}$
denotes the (irreducible, unitary) adduced representation defined in [Reference SahiSah89] (cf. [Reference BaruchBar03]).
For non-archimedean
![]() $\mathbb{F}$
, the theorem follows from [Reference Bernstein and ZelevinskyBZ77] since
$\mathbb{F}$
, the theorem follows from [Reference Bernstein and ZelevinskyBZ77] since
![]() $E^{d}$
coincides with the highest Bernstein–Zelevinsky derivative considered in [Reference Bernstein and ZelevinskyBZ77].
$E^{d}$
coincides with the highest Bernstein–Zelevinsky derivative considered in [Reference Bernstein and ZelevinskyBZ77].
For archimedean
![]() $\mathbb{F}$
,
$\mathbb{F}$
,
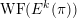 $\operatorname{WF}(E^{k}(\unicode[STIX]{x1D70B}))$
is calculated in [Reference Gourevitch and SahiGS15]. In particular, [Reference Gourevitch and SahiGS15, Theorem 5.0.5] implies the following result.
$\operatorname{WF}(E^{k}(\unicode[STIX]{x1D70B}))$
is calculated in [Reference Gourevitch and SahiGS15]. In particular, [Reference Gourevitch and SahiGS15, Theorem 5.0.5] implies the following result.
Theorem 4.5.2. Let
![]() $\mathbb{F}$
be archimedean and let
$\mathbb{F}$
be archimedean and let
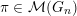 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
. Suppose that
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}(G_{n})$
. Suppose that
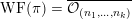 $\operatorname{WF}(\unicode[STIX]{x1D70B})=\overline{{\mathcal{O}}_{(n_{1},\ldots ,n_{k})}}$
with
$\operatorname{WF}(\unicode[STIX]{x1D70B})=\overline{{\mathcal{O}}_{(n_{1},\ldots ,n_{k})}}$
with
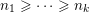 $n_{1}\geqslant \cdots \geqslant n_{k}$
. Then
$n_{1}\geqslant \cdots \geqslant n_{k}$
. Then
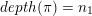 $depth(\unicode[STIX]{x1D70B})=n_{1}$
and
$depth(\unicode[STIX]{x1D70B})=n_{1}$
and
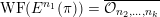 $\operatorname{WF}(E^{n_{1}}(\unicode[STIX]{x1D70B}))=\overline{{\mathcal{O}}_{n_{2},\ldots ,n_{k}}}$
.
$\operatorname{WF}(E^{n_{1}}(\unicode[STIX]{x1D70B}))=\overline{{\mathcal{O}}_{n_{2},\ldots ,n_{k}}}$
.
4.5.2 Proof of Corollary G
Let
![]() $\unicode[STIX]{x1D706}$
be a partition of
$\unicode[STIX]{x1D706}$
be a partition of
![]() $n$
and
$n$
and
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
be the corresponding nilpotent orbit. Denote
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
be the corresponding nilpotent orbit. Denote
 ${\mathcal{W}}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D70B}):=(E^{\unicode[STIX]{x1D706}_{k}}(\ldots E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})\ldots \,))^{\ast }$
. We use Theorem F and identify
${\mathcal{W}}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D70B}):=(E^{\unicode[STIX]{x1D706}_{k}}(\ldots E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})\ldots \,))^{\ast }$
. We use Theorem F and identify
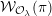 ${\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D70B})$
with
${\mathcal{W}}_{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(\unicode[STIX]{x1D70B})$
with
![]() ${\mathcal{W}}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D70B})$
. We prove the theorem by induction on
${\mathcal{W}}_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D70B})$
. We prove the theorem by induction on
![]() $n$
, using Theorems 4.5.1 and 4.5.2. For the base of the induction we note that
$n$
, using Theorems 4.5.1 and 4.5.2. For the base of the induction we note that
![]() ${\mathcal{M}}(G_{0})$
is the category of finite-dimensional vector spaces, and monomial or irreducible representations of
${\mathcal{M}}(G_{0})$
is the category of finite-dimensional vector spaces, and monomial or irreducible representations of
![]() $G_{0}$
are one-dimensional. For the induction step, let
$G_{0}$
are one-dimensional. For the induction step, let
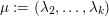 $\unicode[STIX]{x1D707}:=(\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{k})$
and note that by Theorem 4.5.1
$\unicode[STIX]{x1D707}:=(\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{k})$
and note that by Theorem 4.5.1
![]() $E^{\unicode[STIX]{x1D706}_{1}}$
is an exact functor from
$E^{\unicode[STIX]{x1D706}_{1}}$
is an exact functor from
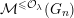 ${\mathcal{M}}^{{\leqslant}{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(G_{n})$
to
${\mathcal{M}}^{{\leqslant}{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(G_{n})$
to
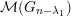 ${\mathcal{M}}(G_{n-\unicode[STIX]{x1D706}_{1}})$
. By Theorem 4.5.2, it maps
${\mathcal{M}}(G_{n-\unicode[STIX]{x1D706}_{1}})$
. By Theorem 4.5.2, it maps
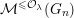 ${\mathcal{M}}^{{\leqslant}{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(G_{n})$
to
${\mathcal{M}}^{{\leqslant}{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(G_{n})$
to
 ${\mathcal{M}}^{{\leqslant}{\mathcal{O}}_{\unicode[STIX]{x1D707}}}(G_{n-\unicode[STIX]{x1D706}_{1}})$
, and
${\mathcal{M}}^{{\leqslant}{\mathcal{O}}_{\unicode[STIX]{x1D707}}}(G_{n-\unicode[STIX]{x1D706}_{1}})$
, and
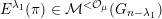 $E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})\in {\mathcal{M}}^{{<}{\mathcal{O}}_{\unicode[STIX]{x1D707}}}(G_{n-\unicode[STIX]{x1D706}_{1}})$
if and only if
$E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})\in {\mathcal{M}}^{{<}{\mathcal{O}}_{\unicode[STIX]{x1D707}}}(G_{n-\unicode[STIX]{x1D706}_{1}})$
if and only if
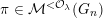 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}^{{<}{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(G_{n})$
. Thus, by the properties of quotient categories (see [Reference GabrielGab62, § III.1]),
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}^{{<}{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(G_{n})$
. Thus, by the properties of quotient categories (see [Reference GabrielGab62, § III.1]),
![]() $E^{\unicode[STIX]{x1D706}_{1}}$
defines an exact and faithful functor from
$E^{\unicode[STIX]{x1D706}_{1}}$
defines an exact and faithful functor from
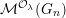 ${\mathcal{M}}^{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(G_{n})$
to
${\mathcal{M}}^{{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(G_{n})$
to
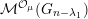 ${\mathcal{M}}^{{\mathcal{O}}_{\unicode[STIX]{x1D707}}}(G_{n-\unicode[STIX]{x1D706}_{1}})$
. Theorem 4.5.1 also implies that if
${\mathcal{M}}^{{\mathcal{O}}_{\unicode[STIX]{x1D707}}}(G_{n-\unicode[STIX]{x1D706}_{1}})$
. Theorem 4.5.1 also implies that if
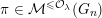 $\unicode[STIX]{x1D70B}\in {\mathcal{M}}^{{\leqslant}{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(G_{n})$
is monomial, then so is
$\unicode[STIX]{x1D70B}\in {\mathcal{M}}^{{\leqslant}{\mathcal{O}}_{\unicode[STIX]{x1D706}}}(G_{n})$
is monomial, then so is
![]() $E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})$
and if
$E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})$
and if
![]() $\unicode[STIX]{x1D70B}$
is irreducible unitarizable, then so is
$\unicode[STIX]{x1D70B}$
is irreducible unitarizable, then so is
![]() $E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})$
. By the induction step,
$E^{\unicode[STIX]{x1D706}_{1}}(\unicode[STIX]{x1D70B})$
. By the induction step,
![]() ${\mathcal{W}}_{\unicode[STIX]{x1D707}}$
defines an exact and faithful functor from
${\mathcal{W}}_{\unicode[STIX]{x1D707}}$
defines an exact and faithful functor from
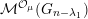 ${\mathcal{M}}^{{\mathcal{O}}_{\unicode[STIX]{x1D707}}}(G_{n-\unicode[STIX]{x1D706}_{1}})$
to the category of finite-dimensional vector spaces, and
${\mathcal{M}}^{{\mathcal{O}}_{\unicode[STIX]{x1D707}}}(G_{n-\unicode[STIX]{x1D706}_{1}})$
to the category of finite-dimensional vector spaces, and
![]() ${\mathcal{W}}_{\unicode[STIX]{x1D707}}$
maps monomial representations and irreducible unitarizable representations to one-dimensional spaces. Thus, so does
${\mathcal{W}}_{\unicode[STIX]{x1D707}}$
maps monomial representations and irreducible unitarizable representations to one-dimensional spaces. Thus, so does
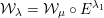 ${\mathcal{W}}_{\unicode[STIX]{x1D706}}={\mathcal{W}}_{\unicode[STIX]{x1D707}}\circ E^{\unicode[STIX]{x1D706}_{1}}$
.◻
${\mathcal{W}}_{\unicode[STIX]{x1D706}}={\mathcal{W}}_{\unicode[STIX]{x1D707}}\circ E^{\unicode[STIX]{x1D706}_{1}}$
.◻
5 Choice-free definitions
5.1 Generalized Whittaker models
In this section we define the generalized Whittaker model corresponding to a nilpotent element
![]() $e\in \mathfrak{g}$
, without choosing a neutral element
$e\in \mathfrak{g}$
, without choosing a neutral element
![]() $h$
. First of all, the filtration
$h$
. First of all, the filtration
![]() $\mathfrak{g}_{{\geqslant}k}$
(unlike the grading
$\mathfrak{g}_{{\geqslant}k}$
(unlike the grading
![]() $\mathfrak{g}_{k}$
) can be defined without choosing
$\mathfrak{g}_{k}$
) can be defined without choosing
![]() $h$
. It is, in fact, called the Deligne filtration and by [Reference DeligneDel80, § I.6] is uniquely defined by the properties:
$h$
. It is, in fact, called the Deligne filtration and by [Reference DeligneDel80, § I.6] is uniquely defined by the properties:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{ad}(e)(\mathfrak{g}_{{\geqslant}k})\subset \mathfrak{g}_{{\geqslant}k+2}\text{ and }\text{ad}(e)^{k}\text{ induces an isomorphism }\mathfrak{g}_{{\geqslant}-k}/\mathfrak{g}_{{\geqslant}-k+1}\simeq \mathfrak{g}_{{\geqslant}k}/\mathfrak{g}_{{\geqslant}k+1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{ad}(e)(\mathfrak{g}_{{\geqslant}k})\subset \mathfrak{g}_{{\geqslant}k+2}\text{ and }\text{ad}(e)^{k}\text{ induces an isomorphism }\mathfrak{g}_{{\geqslant}-k}/\mathfrak{g}_{{\geqslant}-k+1}\simeq \mathfrak{g}_{{\geqslant}k}/\mathfrak{g}_{{\geqslant}k+1}.\end{eqnarray}$$
It is easy to see that this filtration can be defined explicitly by
 $$\begin{eqnarray}\mathfrak{g}_{{\geqslant}k}:=\mathop{\sum }_{i\geqslant \max (1-k,1)}(\text{Ker}(\text{ad}(e)^{i})\cap \text{Im}(\text{ad}(e)^{i+k-1})).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}_{{\geqslant}k}:=\mathop{\sum }_{i\geqslant \max (1-k,1)}(\text{Ker}(\text{ad}(e)^{i})\cap \text{Im}(\text{ad}(e)^{i+k-1})).\end{eqnarray}$$
We will sometimes denote this also by
![]() $\mathfrak{g}_{{>}k-1}$
or by
$\mathfrak{g}_{{>}k-1}$
or by
![]() $\mathfrak{g}_{e,\geqslant k}$
.
$\mathfrak{g}_{e,\geqslant k}$
.
Let
![]() $e^{\bot }$
denote the orthogonal complement to
$e^{\bot }$
denote the orthogonal complement to
![]() $\{e\}$
under the Killing form
$\{e\}$
under the Killing form
![]() $\langle \cdot ,\cdot \rangle$
and let
$\langle \cdot ,\cdot \rangle$
and let
 $$\begin{eqnarray}\mathfrak{u}:=\mathfrak{g}_{{\geqslant}1},\quad \mathfrak{v}:=\mathfrak{g}_{{>}1},\quad I:=\text{ad}(e)^{2}(e^{\bot })\cap \mathfrak{v}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{u}:=\mathfrak{g}_{{\geqslant}1},\quad \mathfrak{v}:=\mathfrak{g}_{{>}1},\quad I:=\text{ad}(e)^{2}(e^{\bot })\cap \mathfrak{v}.\end{eqnarray}$$
Lemma 5.1.1. We have:
-
(i)
 $I$
is an ideal in
$I$
is an ideal in
 $\mathfrak{u}$
;
$\mathfrak{u}$
; -
(ii)
 $\dim \mathfrak{v}/I=1$
and
$\dim \mathfrak{v}/I=1$
and
 $e\notin I$
;
$e\notin I$
; -
(iii) there exists a unique symplectic form
 $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
 $\mathfrak{u}/\mathfrak{v}$
such that for any
$\mathfrak{u}/\mathfrak{v}$
such that for any
 $a,b\in \mathfrak{u}$
we have
$a,b\in \mathfrak{u}$
we have
 $[a,b]-\unicode[STIX]{x1D714}(\bar{a},\bar{b})e\in I$
, where
$[a,b]-\unicode[STIX]{x1D714}(\bar{a},\bar{b})e\in I$
, where
 $\bar{a}$
and
$\bar{a}$
and
 $\bar{b}$
denote the classes of
$\bar{b}$
denote the classes of
 $a$
and
$a$
and
 $b$
;
$b$
; -
(iv)
 $\mathfrak{u}/I$
is a Heisenberg Lie algebra, and its center is spanned by class
$\mathfrak{u}/I$
is a Heisenberg Lie algebra, and its center is spanned by class
 $\bar{e}$
of
$\bar{e}$
of
 $e$
.
$e$
.
Proof. Note that
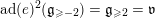 $\text{ad}(e)^{2}(\mathfrak{g}_{{\geqslant}-2})=\mathfrak{g}_{{\geqslant}2}=\mathfrak{v}$
and
$\text{ad}(e)^{2}(\mathfrak{g}_{{\geqslant}-2})=\mathfrak{g}_{{\geqslant}2}=\mathfrak{v}$
and
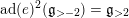 $\text{ad}(e)^{2}(\mathfrak{g}_{{>}-2})=\mathfrak{g}_{{>}2}$
. Pick an
$\text{ad}(e)^{2}(\mathfrak{g}_{{>}-2})=\mathfrak{g}_{{>}2}$
. Pick an
![]() $\mathfrak{sl}_{2}$
-triple
$\mathfrak{sl}_{2}$
-triple
![]() $(f,h,e)$
. Using the
$(f,h,e)$
. Using the
![]() $h$
-grading it is easy to see that
$h$
-grading it is easy to see that
![]() $\mathfrak{g}_{{\geqslant}k}$
is a Lie algebra filtration.
$\mathfrak{g}_{{\geqslant}k}$
is a Lie algebra filtration.
(i) We have
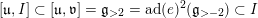 $[\mathfrak{u},I]\subset [\mathfrak{u},\mathfrak{v}]=\mathfrak{g}_{{>}2}=\text{ad}(e)^{2}(\mathfrak{g}_{{>}-2})\subset I$
.
$[\mathfrak{u},I]\subset [\mathfrak{u},\mathfrak{v}]=\mathfrak{g}_{{>}2}=\text{ad}(e)^{2}(\mathfrak{g}_{{>}-2})\subset I$
.
(ii) Since
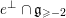 $e^{\bot }\cap \mathfrak{g}_{{\geqslant}-2}$
has codimension at most 1 in
$e^{\bot }\cap \mathfrak{g}_{{\geqslant}-2}$
has codimension at most 1 in
![]() $\mathfrak{g}_{{\geqslant}-2}$
,
$\mathfrak{g}_{{\geqslant}-2}$
,
![]() $I$
has codimension at most 1 in
$I$
has codimension at most 1 in
![]() $\mathfrak{v}$
. Thus, it is enough to show that
$\mathfrak{v}$
. Thus, it is enough to show that
![]() $e\notin I$
, i.e. if
$e\notin I$
, i.e. if
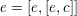 $e=[e,[e,c]]$
, then
$e=[e,[e,c]]$
, then
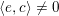 $\langle e,c\rangle \neq 0$
. Since
$\langle e,c\rangle \neq 0$
. Since
![]() $\text{ad}(h)$
has integer eigenvalues,
$\text{ad}(h)$
has integer eigenvalues,
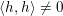 $\langle h,h\rangle \neq 0$
. Now
$\langle h,h\rangle \neq 0$
. Now
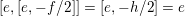 $[e,[e,-f/2]]=[e,-h/2]=e$
and
$[e,[e,-f/2]]=[e,-h/2]=e$
and
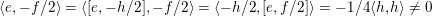 $\langle e,-f/2\rangle =\langle [e,-h/2],-f/2\rangle =\langle -h/2,[e,f/2]\rangle =-1/4\langle h,h\rangle \neq 0$
. Now,
$\langle e,-f/2\rangle =\langle [e,-h/2],-f/2\rangle =\langle -h/2,[e,f/2]\rangle =-1/4\langle h,h\rangle \neq 0$
. Now,
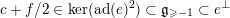 $c+f/2\in \ker (\text{ad}(e)^{2})\subset \mathfrak{g}_{{\geqslant}-1}\subset e^{\bot }$
, thus
$c+f/2\in \ker (\text{ad}(e)^{2})\subset \mathfrak{g}_{{\geqslant}-1}\subset e^{\bot }$
, thus
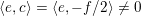 $\langle e,c\rangle =\langle e,-f/2\rangle \neq 0$
.
$\langle e,c\rangle =\langle e,-f/2\rangle \neq 0$
.
(iii) Let
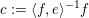 $c:=\langle f,e\rangle ^{-1}f$
and define
$c:=\langle f,e\rangle ^{-1}f$
and define
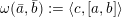 $\unicode[STIX]{x1D714}(\bar{a},\bar{b}):=\langle c,[a,b]\rangle$
. It is easy to see that
$\unicode[STIX]{x1D714}(\bar{a},\bar{b}):=\langle c,[a,b]\rangle$
. It is easy to see that
![]() $\unicode[STIX]{x1D714}$
is the only anti-symmetric form satisfying
$\unicode[STIX]{x1D714}$
is the only anti-symmetric form satisfying
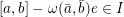 $[a,b]-\unicode[STIX]{x1D714}(\bar{a},\bar{b})e\in I$
. Let us show that
$[a,b]-\unicode[STIX]{x1D714}(\bar{a},\bar{b})e\in I$
. Let us show that
![]() $\unicode[STIX]{x1D714}$
is non-degenerate. Let
$\unicode[STIX]{x1D714}$
is non-degenerate. Let
![]() $a\in \mathfrak{u}$
such that
$a\in \mathfrak{u}$
such that
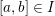 $[a,b]\in I$
for any
$[a,b]\in I$
for any
![]() $b\in \mathfrak{u}$
. This implies
$b\in \mathfrak{u}$
. This implies
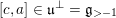 $[c,a]\in \mathfrak{u}^{\bot }=\mathfrak{g}_{{>}-1}$
and thus
$[c,a]\in \mathfrak{u}^{\bot }=\mathfrak{g}_{{>}-1}$
and thus
![]() $a\in \mathfrak{v}$
.
$a\in \mathfrak{v}$
.
(iv) This follows immediately from part (iii). ◻
Definition 5.1.2. We now define a character of the center of
![]() $\mathfrak{u}/I$
by requiring it to be 1 on
$\mathfrak{u}/I$
by requiring it to be 1 on
![]() $\bar{e}$
, consider the corresponding oscillator representation of the Lie group
$\bar{e}$
, consider the corresponding oscillator representation of the Lie group
 $\text{Exp}(\mathfrak{u}/I)$
and lift it to an irreducible representation
$\text{Exp}(\mathfrak{u}/I)$
and lift it to an irreducible representation
![]() ${\mathcal{S}}_{e}$
of
${\mathcal{S}}_{e}$
of
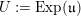 $U:=\text{Exp}(\mathfrak{u})$
. We then define the generalized Whittaker model associated to
$U:=\text{Exp}(\mathfrak{u})$
. We then define the generalized Whittaker model associated to
![]() $e$
by
$e$
by
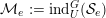 ${\mathcal{M}}_{e}:=\text{ind}_{U}^{G}({\mathcal{S}}_{e})$
.
${\mathcal{M}}_{e}:=\text{ind}_{U}^{G}({\mathcal{S}}_{e})$
.
The connection to the generalized Whittaker models
![]() ${\mathcal{W}}_{f}$
is given by the following straightforward lemma.
${\mathcal{W}}_{f}$
is given by the following straightforward lemma.
Lemma 5.1.3. Let
![]() $(f,h,e)$
be an
$(f,h,e)$
be an
![]() $\mathfrak{sl}_{2}$
-triple and define
$\mathfrak{sl}_{2}$
-triple and define
![]() $\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
by
$\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
by
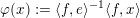 $\unicode[STIX]{x1D711}(x):=\langle f,e\rangle ^{-1}\langle f,x\rangle$
. Then
$\unicode[STIX]{x1D711}(x):=\langle f,e\rangle ^{-1}\langle f,x\rangle$
. Then
![]() ${\mathcal{M}}_{e}$
is naturally isomorphic to
${\mathcal{M}}_{e}$
is naturally isomorphic to
![]() ${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
.
${\mathcal{W}}_{\unicode[STIX]{x1D711}}$
.
Remark 5.1.4. The analogous approach in positive characteristic immediately faces two problems: exponentials not being defined and the Killing form being degenerate. However, for
![]() $\mathfrak{g}=\mathfrak{g}_{n}$
we can replace the Killing form by the trace form, and try to replace the exponential by the map
$\mathfrak{g}=\mathfrak{g}_{n}$
we can replace the Killing form by the trace form, and try to replace the exponential by the map
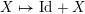 $X\mapsto \text{Id}+X$
. Then the next question is whether Lemma 5.1.1 holds. One can show that in three cases it fails completely: if
$X\mapsto \text{Id}+X$
. Then the next question is whether Lemma 5.1.1 holds. One can show that in three cases it fails completely: if
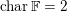 $\text{char}\,\mathbb{F}=2$
,
$\text{char}\,\mathbb{F}=2$
,
![]() $n\geqslant 3$
, if
$n\geqslant 3$
, if
 $\text{char}\,\mathbb{F}=3$
,
$\text{char}\,\mathbb{F}=3$
,
![]() $n\geqslant 8$
, or if
$n\geqslant 8$
, or if
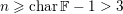 $n\geqslant \text{char}\,\mathbb{F}-1>3$
. In these cases there exists
$n\geqslant \text{char}\,\mathbb{F}-1>3$
. In these cases there exists
![]() $e\in \mathfrak{g}_{n}$
such that
$e\in \mathfrak{g}_{n}$
such that
![]() $e\in \mathfrak{g}_{{\geqslant}3}$
and
$e\in \mathfrak{g}_{{\geqslant}3}$
and
![]() $I=\mathfrak{v}$
. We also see in these cases that the Deligne filtration is not a Lie algebra filtration.
$I=\mathfrak{v}$
. We also see in these cases that the Deligne filtration is not a Lie algebra filtration.
In other cases we have, for any
![]() $e\in \mathfrak{g}$
,
$e\in \mathfrak{g}$
,
![]() $e\in \mathfrak{g}_{{\geqslant}2}$
but
$e\in \mathfrak{g}_{{\geqslant}2}$
but
![]() $e\notin \mathfrak{g}_{{\geqslant}3}$
. It is not clear whether
$e\notin \mathfrak{g}_{{\geqslant}3}$
. It is not clear whether
![]() $\mathfrak{u}$
and
$\mathfrak{u}$
and
![]() $\mathfrak{v}$
are always Lie subalgebras or whether
$\mathfrak{v}$
are always Lie subalgebras or whether
![]() $I$
is an ideal in
$I$
is an ideal in
![]() $\mathfrak{u}$
. However, any
$\mathfrak{u}$
. However, any
![]() $e\in \mathfrak{g}_{n}$
can be completed to an
$e\in \mathfrak{g}_{n}$
can be completed to an
![]() $\mathfrak{sl}_{2}$
-triple. Using this triple, one can show that if
$\mathfrak{sl}_{2}$
-triple. Using this triple, one can show that if
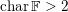 $\text{char}\,\mathbb{F}>2$
and
$\text{char}\,\mathbb{F}>2$
and
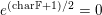 $e^{(\text{char}\,\mathbb{F}+1)/2}=0$
, then Lemma 5.1.1 holds,
$e^{(\text{char}\,\mathbb{F}+1)/2}=0$
, then Lemma 5.1.1 holds,
![]() $\text{Id}+\mathfrak{u}$
forms a subgroup of
$\text{Id}+\mathfrak{u}$
forms a subgroup of
![]() $G$
which includes
$G$
which includes
![]() $\text{Id}+I$
as a normal subgroup,
$\text{Id}+I$
as a normal subgroup,
![]() $e$
defines a central character of the Heisenberg group
$e$
defines a central character of the Heisenberg group
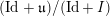 $(\text{Id}+\mathfrak{u})/(\text{Id}+I)$
and one can consider the corresponding oscillator representation and Whittaker model.
$(\text{Id}+\mathfrak{u})/(\text{Id}+I)$
and one can consider the corresponding oscillator representation and Whittaker model.
5.2 Degenerate Whittaker models
Let
![]() $Z$
be a rational semi-simple element that commutes with
$Z$
be a rational semi-simple element that commutes with
![]() $e$
. For any
$e$
. For any
![]() $t\in \mathbb{Q}$
define
$t\in \mathbb{Q}$
define
 $$\begin{eqnarray}\mathfrak{g}_{{\geqslant}t}^{e,Z}:=\mathop{\sum }_{i}\biggl(\mathfrak{g}_{{\geqslant}i}\cap \mathop{\sum }_{s\geqslant t-i}\mathfrak{g}_{s}^{Z}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}_{{\geqslant}t}^{e,Z}:=\mathop{\sum }_{i}\biggl(\mathfrak{g}_{{\geqslant}i}\cap \mathop{\sum }_{s\geqslant t-i}\mathfrak{g}_{s}^{Z}\biggr).\end{eqnarray}$$
Note the following straightforward lemma.
Lemma 5.2.1. If
![]() $h\in \mathfrak{g}_{Z}$
is a neutral element for
$h\in \mathfrak{g}_{Z}$
is a neutral element for
![]() $e$
, then
$e$
, then
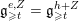 $\mathfrak{g}_{{\geqslant}t}^{e,Z}=\mathfrak{g}_{{\geqslant}t}^{h+Z}$
.
$\mathfrak{g}_{{\geqslant}t}^{e,Z}=\mathfrak{g}_{{\geqslant}t}^{h+Z}$
.
In fact, commuting
![]() $e$
and
$e$
and
![]() $Z$
is the same amount of information as the Lie algebra element
$Z$
is the same amount of information as the Lie algebra element
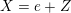 $X=e+Z$
. We can reformulate the filtration in terms of
$X=e+Z$
. We can reformulate the filtration in terms of
![]() $X$
. First define
$X$
. First define
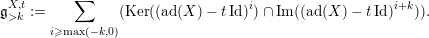 $$\begin{eqnarray}\mathfrak{g}_{{>}k}^{X,t}:=\mathop{\sum }_{i\geqslant \max (-k,0)}(\text{Ker}((\text{ad}(X)-t\,\text{Id})^{i})\cap \text{Im}((\text{ad}(X)-t\,\text{Id})^{i+k})).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}_{{>}k}^{X,t}:=\mathop{\sum }_{i\geqslant \max (-k,0)}(\text{Ker}((\text{ad}(X)-t\,\text{Id})^{i})\cap \text{Im}((\text{ad}(X)-t\,\text{Id})^{i+k})).\end{eqnarray}$$
The following lemma is straightforward.
Lemma 5.2.2. We have
 $$\begin{eqnarray}\mathfrak{g}_{{>}k}^{X,t}=\mathfrak{g}_{t}^{Z}\cap \mathfrak{g}_{{>}k}^{e}\quad \text{and}\quad \mathfrak{g}_{{>}t}^{e,Z}=\mathop{\sum }_{i}\mathop{\sum }_{t\geqslant s-i}\mathfrak{g}_{{>}i}^{X,t}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}_{{>}k}^{X,t}=\mathfrak{g}_{t}^{Z}\cap \mathfrak{g}_{{>}k}^{e}\quad \text{and}\quad \mathfrak{g}_{{>}t}^{e,Z}=\mathop{\sum }_{i}\mathop{\sum }_{t\geqslant s-i}\mathfrak{g}_{{>}i}^{X,t}.\end{eqnarray}$$
Now define
 $$\begin{eqnarray}\mathfrak{u}:=\mathfrak{g}_{{\geqslant}1}^{e,Z},\quad \mathfrak{v}:=\mathfrak{g}_{{>}1}^{e,Z},\quad I:=\text{ad}(X)^{2}(e^{\bot })\cap \mathfrak{v},\quad J:=I+\text{ad}(X)(\mathfrak{u}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{u}:=\mathfrak{g}_{{\geqslant}1}^{e,Z},\quad \mathfrak{v}:=\mathfrak{g}_{{>}1}^{e,Z},\quad I:=\text{ad}(X)^{2}(e^{\bot })\cap \mathfrak{v},\quad J:=I+\text{ad}(X)(\mathfrak{u}).\end{eqnarray}$$
Lemma 5.2.3. The space
![]() $J$
is an ideal in
$J$
is an ideal in
![]() $\mathfrak{u}$
, and the algebra
$\mathfrak{u}$
, and the algebra
![]() $\mathfrak{u}/J$
is isomorphic to the Heisenberg algebra defined in § 5.1 using the element
$\mathfrak{u}/J$
is isomorphic to the Heisenberg algebra defined in § 5.1 using the element
![]() $e$
of the Lie algebra
$e$
of the Lie algebra
![]() $\mathfrak{g}_{Z}$
.
$\mathfrak{g}_{Z}$
.
Proof. Note that for any
![]() $t\neq 0$
, we have
$t\neq 0$
, we have
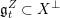 $\mathfrak{g}_{t}^{Z}\subset X^{\bot }$
and
$\mathfrak{g}_{t}^{Z}\subset X^{\bot }$
and
![]() $\text{ad}(X)$
is invertible on
$\text{ad}(X)$
is invertible on
![]() $\mathfrak{g}_{t}^{Z}$
. Thus,
$\mathfrak{g}_{t}^{Z}$
. Thus,
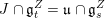 $J\cap \mathfrak{g}_{t}^{Z}=\mathfrak{u}\cap \mathfrak{g}_{s}^{Z}$
.
$J\cap \mathfrak{g}_{t}^{Z}=\mathfrak{u}\cap \mathfrak{g}_{s}^{Z}$
.
To see that
![]() $J$
is an ideal in
$J$
is an ideal in
![]() $\mathfrak{u}$
, let
$\mathfrak{u}$
, let
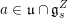 $a\in \mathfrak{u}\cap \mathfrak{g}_{s}^{Z}$
and
$a\in \mathfrak{u}\cap \mathfrak{g}_{s}^{Z}$
and
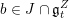 $b\in J\cap \mathfrak{g}_{t}^{Z}$
. Then
$b\in J\cap \mathfrak{g}_{t}^{Z}$
. Then
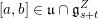 $[a,b]\in \mathfrak{u}\cap \mathfrak{g}_{s+t}^{Z}$
, which lies in
$[a,b]\in \mathfrak{u}\cap \mathfrak{g}_{s+t}^{Z}$
, which lies in
![]() $J$
unless
$J$
unless
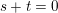 $s+t=0$
. If
$s+t=0$
. If
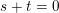 $s+t=0$
, then
$s+t=0$
, then
 $[a,b]\in (\mathfrak{g}^{Z})_{{>}2}$
, which lies in the ideal
$[a,b]\in (\mathfrak{g}^{Z})_{{>}2}$
, which lies in the ideal
![]() $I^{\prime }$
defined by
$I^{\prime }$
defined by
![]() $e$
in
$e$
in
![]() $(\mathfrak{g}^{Z})_{{\geqslant}2}$
.
$(\mathfrak{g}^{Z})_{{\geqslant}2}$
.
We also see that
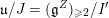 $\mathfrak{u}/J=(\mathfrak{g}^{Z})_{{\geqslant}2}/I^{\prime }$
.◻
$\mathfrak{u}/J=(\mathfrak{g}^{Z})_{{\geqslant}2}/I^{\prime }$
.◻
Definition 5.2.4. Using the isomorphism in Lemma 5.2.3 we define an oscillator representation of the Lie group
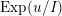 $\text{Exp}(u/I)$
and lift it to an irreducible representation
$\text{Exp}(u/I)$
and lift it to an irreducible representation
![]() $\unicode[STIX]{x1D70E}_{e}$
of
$\unicode[STIX]{x1D70E}_{e}$
of
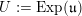 $U:=\text{Exp}(\mathfrak{u})$
. We then define the degenerate Whittaker model associated to
$U:=\text{Exp}(\mathfrak{u})$
. We then define the degenerate Whittaker model associated to
![]() $e$
and
$e$
and
![]() $Z$
by
$Z$
by
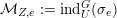 ${\mathcal{M}}_{Z,e}:=\text{ind}_{U}^{G}(\unicode[STIX]{x1D70E}_{e})$
.
${\mathcal{M}}_{Z,e}:=\text{ind}_{U}^{G}(\unicode[STIX]{x1D70E}_{e})$
.
From Lemmas 5.1.3 and 5.2.3 we obtain the following corollary.
Corollary 5.2.5. Let
![]() $Z\in \mathfrak{g}$
be a rational semi-simple element and let
$Z\in \mathfrak{g}$
be a rational semi-simple element and let
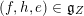 $(f,h,e)\in \mathfrak{g}_{Z}$
be an
$(f,h,e)\in \mathfrak{g}_{Z}$
be an
![]() $\mathfrak{sl}_{2}$
-triple. Let
$\mathfrak{sl}_{2}$
-triple. Let
![]() $\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
be defined by pairing with
$\unicode[STIX]{x1D711}\in \mathfrak{g}^{\ast }$
be defined by pairing with
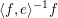 $\langle f,e\rangle ^{-1}f$
. Then
$\langle f,e\rangle ^{-1}f$
. Then
![]() ${\mathcal{M}}_{Z,e}$
is naturally isomorphic to
${\mathcal{M}}_{Z,e}$
is naturally isomorphic to
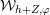 ${\mathcal{W}}_{h+Z,\unicode[STIX]{x1D711}}$
.
${\mathcal{W}}_{h+Z,\unicode[STIX]{x1D711}}$
.
6 Global setting
Let
![]() $K$
be a number field and let
$K$
be a number field and let
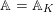 $\mathbb{A}=\mathbb{A}_{K}$
be its ring of adeles. In this section we let
$\mathbb{A}=\mathbb{A}_{K}$
be its ring of adeles. In this section we let
![]() $\unicode[STIX]{x1D712}$
be a non-trivial unitary character of
$\unicode[STIX]{x1D712}$
be a non-trivial unitary character of
![]() $\mathbb{A}$
, which is trivial on
$\mathbb{A}$
, which is trivial on
![]() $K$
. Then
$K$
. Then
![]() $\unicode[STIX]{x1D712}$
defines an isomorphism between
$\unicode[STIX]{x1D712}$
defines an isomorphism between
![]() $\mathbb{A}$
and
$\mathbb{A}$
and
![]() $\hat{\mathbb{A}}$
via the map
$\hat{\mathbb{A}}$
via the map
![]() $a\mapsto \unicode[STIX]{x1D712}_{a}$
, where
$a\mapsto \unicode[STIX]{x1D712}_{a}$
, where
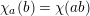 $\unicode[STIX]{x1D712}_{a}(b)=\unicode[STIX]{x1D712}(ab)$
for all
$\unicode[STIX]{x1D712}_{a}(b)=\unicode[STIX]{x1D712}(ab)$
for all
![]() $b\in \mathbb{A}$
. This isomorphism restricts to an isomorphism
$b\in \mathbb{A}$
. This isomorphism restricts to an isomorphism
 $$\begin{eqnarray}\widehat{\mathbb{A}/K}\cong \{\unicode[STIX]{x1D713}\in \hat{\mathbb{A}}\mid \unicode[STIX]{x1D713}|_{K}\equiv 1\}=\{\unicode[STIX]{x1D712}_{a}\mid a\in K\}\cong K.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\mathbb{A}/K}\cong \{\unicode[STIX]{x1D713}\in \hat{\mathbb{A}}\mid \unicode[STIX]{x1D713}|_{K}\equiv 1\}=\{\unicode[STIX]{x1D712}_{a}\mid a\in K\}\cong K.\end{eqnarray}$$
Given an algebraic group
![]() $G$
defined over
$G$
defined over
![]() $K$
we will denote its Lie algebra by
$K$
we will denote its Lie algebra by
![]() $\mathfrak{g}$
and we will denote the group of its adelic (respectively
$\mathfrak{g}$
and we will denote the group of its adelic (respectively
![]() $K$
-rational) points by
$K$
-rational) points by
![]() $G(\mathbb{A})$
(respectively
$G(\mathbb{A})$
(respectively
![]() $G(K)$
). We will also define the Lie algebras
$G(K)$
). We will also define the Lie algebras
![]() $\mathfrak{g}(\mathbb{A})$
and
$\mathfrak{g}(\mathbb{A})$
and
![]() $\mathfrak{g}(K)$
in a similar way.
$\mathfrak{g}(K)$
in a similar way.
Given a Whittaker pair
![]() $(S,\unicode[STIX]{x1D711})$
on
$(S,\unicode[STIX]{x1D711})$
on
![]() $\mathfrak{g}(K)$
, we set
$\mathfrak{g}(K)$
, we set
 $\mathfrak{u}=\mathfrak{g}_{{\geqslant}1}^{S}$
and
$\mathfrak{u}=\mathfrak{g}_{{\geqslant}1}^{S}$
and
![]() $\mathfrak{n}$
to be the radical of the form
$\mathfrak{n}$
to be the radical of the form
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}|_{\mathfrak{u}}$
, where
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}|_{\mathfrak{u}}$
, where
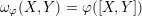 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}(X,Y)=\unicode[STIX]{x1D711}([X,Y])$
, as before. Let
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}(X,Y)=\unicode[STIX]{x1D711}([X,Y])$
, as before. Let
![]() $\mathfrak{l}\subset \mathfrak{u}$
be any choice of a maximal isotropic Lie algebra with respect to this form, and let
$\mathfrak{l}\subset \mathfrak{u}$
be any choice of a maximal isotropic Lie algebra with respect to this form, and let
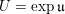 $U=\exp \mathfrak{u}$
,
$U=\exp \mathfrak{u}$
,
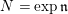 $N=\exp \mathfrak{n}$
and
$N=\exp \mathfrak{n}$
and
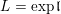 $L=\exp \mathfrak{l}$
. Observe that we can extend
$L=\exp \mathfrak{l}$
. Observe that we can extend
![]() $\unicode[STIX]{x1D711}$
to a linear functional on
$\unicode[STIX]{x1D711}$
to a linear functional on
![]() $\mathfrak{g}(\mathbb{A})$
by linearity and, furthermore, the character
$\mathfrak{g}(\mathbb{A})$
by linearity and, furthermore, the character
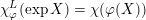 $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(\exp X)=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(X))$
defined on
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(\exp X)=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(X))$
defined on
![]() $L(\mathbb{A})$
is automorphic, that is, it is trivial on
$L(\mathbb{A})$
is automorphic, that is, it is trivial on
![]() $L(K)$
. We will denote its restriction to
$L(K)$
. We will denote its restriction to
![]() $N(\mathbb{A})$
simply by
$N(\mathbb{A})$
simply by
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
.
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
.
Definition 6.0.1. Let
![]() $(S,\unicode[STIX]{x1D711})$
be a Whittaker pair for
$(S,\unicode[STIX]{x1D711})$
be a Whittaker pair for
![]() $\mathfrak{g}(K)$
and let
$\mathfrak{g}(K)$
and let
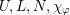 $U,L,N,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
and
$U,L,N,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}$
and
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}$
be as above. For an automorphic function
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}$
be as above. For an automorphic function
![]() $f$
, we define its
$f$
, we define its
![]() $(S,\unicode[STIX]{x1D711})$
-Whittaker–Fourier coefficient to be
$(S,\unicode[STIX]{x1D711})$
-Whittaker–Fourier coefficient to be
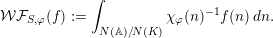 $$\begin{eqnarray}{\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(f):=\int _{N(\mathbb{A})/N(K)}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}(n)^{-1}f(n)\,dn.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(f):=\int _{N(\mathbb{A})/N(K)}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}(n)^{-1}f(n)\,dn.\end{eqnarray}$$
We also define its
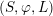 $(S,\unicode[STIX]{x1D711},L)$
-Whittaker–Fourier coefficient to be
$(S,\unicode[STIX]{x1D711},L)$
-Whittaker–Fourier coefficient to be
 $$\begin{eqnarray}{\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(f):=\int _{L(\mathbb{A})/L(K)}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l)^{-1}f(l)\,dl.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(f):=\int _{L(\mathbb{A})/L(K)}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l)^{-1}f(l)\,dl.\end{eqnarray}$$
Observe that
![]() ${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}$
and
${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}$
and
![]() ${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}$
define linear functionals on the space of automorphic forms. If
${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}$
define linear functionals on the space of automorphic forms. If
![]() $(\unicode[STIX]{x1D70B},V_{\unicode[STIX]{x1D70B}})$
is an automorphic representation of
$(\unicode[STIX]{x1D70B},V_{\unicode[STIX]{x1D70B}})$
is an automorphic representation of
![]() $G$
, then we will denote their restrictions to
$G$
, then we will denote their restrictions to
![]() $\unicode[STIX]{x1D70B}$
by
$\unicode[STIX]{x1D70B}$
by
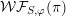 ${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
and
${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})$
and
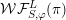 ${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(\unicode[STIX]{x1D70B})$
, respectively.
${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(\unicode[STIX]{x1D70B})$
, respectively.
In order to adapt our arguments to the global setting we will have to replace Lemma 3.2.1 by the following one, which is analogous to [Reference Ginzburg, Rallis and SoudryGRS11, Propositions 7.2 and 7.3].
Lemma 6.0.2. Let
![]() $(\unicode[STIX]{x1D70B},V_{\unicode[STIX]{x1D70B}})$
be an automorphic representation of
$(\unicode[STIX]{x1D70B},V_{\unicode[STIX]{x1D70B}})$
be an automorphic representation of
![]() $G$
. Then
$G$
. Then
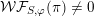 ${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0$
if and only if
${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B})\neq 0$
if and only if
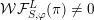 ${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(\unicode[STIX]{x1D70B})\neq 0$
. More specifically, if
${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(\unicode[STIX]{x1D70B})\neq 0$
. More specifically, if
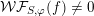 ${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(f)\neq 0$
for some
${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(f)\neq 0$
for some
![]() $f\in \unicode[STIX]{x1D70B}$
, then
$f\in \unicode[STIX]{x1D70B}$
, then
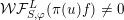 ${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(\unicode[STIX]{x1D70B}(u)f)\neq 0$
for some
${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(\unicode[STIX]{x1D70B}(u)f)\neq 0$
for some
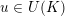 $u\in U(K)$
.
$u\in U(K)$
.
Proof. We assume that
![]() $\unicode[STIX]{x1D711}$
is non-zero since otherwise the statement is a tautology. Let
$\unicode[STIX]{x1D711}$
is non-zero since otherwise the statement is a tautology. Let
![]() $f\in \unicode[STIX]{x1D70B}$
be such that
$f\in \unicode[STIX]{x1D70B}$
be such that
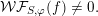 ${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(f)\neq 0.$
Define a function
${\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(f)\neq 0.$
Define a function
![]() $f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}$
on
$f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}$
on
![]() $L$
by
$L$
by
 $$\begin{eqnarray}f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(l)={\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}(l)f)\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(l)={\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D70B}(l)f)\end{eqnarray}$$
and observe that the function
 $(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L})^{-1}\cdot f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}$
is left-invariant under the action of
$(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L})^{-1}\cdot f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}$
is left-invariant under the action of
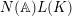 $N(\mathbb{A})L(K)$
. In other words, we can identify
$N(\mathbb{A})L(K)$
. In other words, we can identify
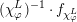 $(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L})^{-1}\cdot f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}$
with a function on
$(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L})^{-1}\cdot f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}$
with a function on
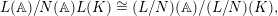 $$\begin{eqnarray}L(\mathbb{A})/N(\mathbb{A})L(K)\cong (L/N)(\mathbb{A})/(L/N)(K),\end{eqnarray}$$
$$\begin{eqnarray}L(\mathbb{A})/N(\mathbb{A})L(K)\cong (L/N)(\mathbb{A})/(L/N)(K),\end{eqnarray}$$
where the equality follows from the fact that
![]() $L/N$
is abelian. Therefore, we have a Fourier series expansion
$L/N$
is abelian. Therefore, we have a Fourier series expansion
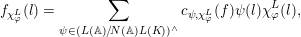 $$\begin{eqnarray}f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(l)=\mathop{\sum }_{\unicode[STIX]{x1D713}\in (L(\mathbb{A})/N(\mathbb{A})L(K))^{\wedge }}c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(f)\unicode[STIX]{x1D713}(l)\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l),\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(l)=\mathop{\sum }_{\unicode[STIX]{x1D713}\in (L(\mathbb{A})/N(\mathbb{A})L(K))^{\wedge }}c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(f)\unicode[STIX]{x1D713}(l)\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l),\end{eqnarray}$$
where
 $$\begin{eqnarray}c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(f)=\int _{L(\mathbb{A})/L(K)}\unicode[STIX]{x1D713}(l)^{-1}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l)^{-1}f(l)\,dl.\end{eqnarray}$$
$$\begin{eqnarray}c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(f)=\int _{L(\mathbb{A})/L(K)}\unicode[STIX]{x1D713}(l)^{-1}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l)^{-1}f(l)\,dl.\end{eqnarray}$$
Since
 $$\begin{eqnarray}0\neq {\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(f)=f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(e)=\mathop{\sum }_{\unicode[STIX]{x1D713}\in (L(\mathbb{A})/N(\mathbb{A})L(K))^{\wedge }}c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(f),\end{eqnarray}$$
$$\begin{eqnarray}0\neq {\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(f)=f_{\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(e)=\mathop{\sum }_{\unicode[STIX]{x1D713}\in (L(\mathbb{A})/N(\mathbb{A})L(K))^{\wedge }}c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(f),\end{eqnarray}$$
we conclude that at least one of the coefficients
 $c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(f)$
is different from 0.
$c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(f)$
is different from 0.
Now observe that the map
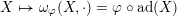 $X\mapsto \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}(X,\cdot )=\unicode[STIX]{x1D711}\circ \text{ad}(X)$
induces an isomorphism between
$X\mapsto \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}(X,\cdot )=\unicode[STIX]{x1D711}\circ \text{ad}(X)$
induces an isomorphism between
![]() $\mathfrak{u}/\mathfrak{l}$
and
$\mathfrak{u}/\mathfrak{l}$
and
![]() $(\mathfrak{l}/\mathfrak{n})^{\prime }$
. Hence, according to (39) and (42), we can use the character
$(\mathfrak{l}/\mathfrak{n})^{\prime }$
. Hence, according to (39) and (42), we can use the character
![]() $\unicode[STIX]{x1D712}$
to define a group isomorphism
$\unicode[STIX]{x1D712}$
to define a group isomorphism
 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}(U/L)(K) & \longrightarrow & (L(\mathbb{A})/N(\mathbb{A})L(K))^{\wedge }\\ u & \mapsto & \unicode[STIX]{x1D713}_{u},\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}(U/L)(K) & \longrightarrow & (L(\mathbb{A})/N(\mathbb{A})L(K))^{\wedge }\\ u & \mapsto & \unicode[STIX]{x1D713}_{u},\end{array}\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{u}(l)=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}([X,Y])),\quad u=\exp X\quad \text{and}\quad l=\exp Y.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{u}(l)=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}([X,Y])),\quad u=\exp X\quad \text{and}\quad l=\exp Y.\end{eqnarray}$$
Hence, for all
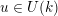 $u\in U(k)$
and
$u\in U(k)$
and
![]() $l\in L$
we have
$l\in L$
we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{u}(l)\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l) & = & \displaystyle \unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}([X,Y]))\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(Y))=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(Y+[X,Y]))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(e^{\text{ad}(X)}(Y)))=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(\text{Ad}(u)Y))=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(ulu^{-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{u}(l)\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l) & = & \displaystyle \unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}([X,Y]))\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(Y))=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(Y+[X,Y]))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(e^{\text{ad}(X)}(Y)))=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}(\text{Ad}(u)Y))=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(ulu^{-1}).\nonumber\end{eqnarray}$$
Here we are taking again
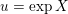 $u=\exp X$
,
$u=\exp X$
,
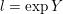 $l=\exp Y$
and the middle equality follows from the vanishing of
$l=\exp Y$
and the middle equality follows from the vanishing of
![]() $\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D711}$
on
![]() $\mathfrak{g}_{{>}2}^{S}$
. But now, from formula (44) and the fact that
$\mathfrak{g}_{{>}2}^{S}$
. But now, from formula (44) and the fact that
![]() $f$
is automorphic, we have
$f$
is automorphic, we have
 $$\begin{eqnarray}\displaystyle c_{\unicode[STIX]{x1D713}_{u},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(f) & = & \displaystyle \int _{L(\mathbb{A})/L(K)}\unicode[STIX]{x1D713}_{u}(l)^{-1}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l)^{-1}f(l)\,dl=\int _{L(\mathbb{A})/L(K)}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(ulu^{-1})^{-1}f(l)\,dl\nonumber\\ \displaystyle & = & \displaystyle \int _{L(\mathbb{A})/L(K)}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l)^{-1}f(u^{-1}lu)\,dl={\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(\unicode[STIX]{x1D70B}(u)f),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{\unicode[STIX]{x1D713}_{u},\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}}(f) & = & \displaystyle \int _{L(\mathbb{A})/L(K)}\unicode[STIX]{x1D713}_{u}(l)^{-1}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l)^{-1}f(l)\,dl=\int _{L(\mathbb{A})/L(K)}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(ulu^{-1})^{-1}f(l)\,dl\nonumber\\ \displaystyle & = & \displaystyle \int _{L(\mathbb{A})/L(K)}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{L}(l)^{-1}f(u^{-1}lu)\,dl={\mathcal{W}}{\mathcal{F}}_{S,\unicode[STIX]{x1D711}}^{L}(\unicode[STIX]{x1D70B}(u)f),\nonumber\end{eqnarray}$$
for all
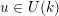 $u\in U(k)$
. Since we have already seen that at least one of these coefficients is non-zero, we obtain the result claimed in the lemma.◻
$u\in U(k)$
. Since we have already seen that at least one of these coefficients is non-zero, we obtain the result claimed in the lemma.◻
The rest of the proof of Theorem A can be applied in the adelic setting, with the appropriate modifications. This implies Theorem C.
Acknowledgements
We thank Avraham Aizenbud, Joseph Bernstein, Wee Teck Gan, Crystal Hoyt, Erez Lapid, Ivan Loseu, David Soudry, Birgit Speh and Cheng-Bo Zhu for fruitful discussions, and Baying Liu and the anonymous referee for useful remarks.
This paper was conceived during the workshop ‘Representation Theory and Analysis of Reductive Groups: Spherical Spaces and Hecke Algebras’ at Oberwolfach in January 2014. We would like to thank the organizers of the workshop Bernhard Kroetz, Eric Opdam, Henrik Schlichtkrull and Peter Trapa; and the administration of the MFO for inviting us and for the warm and stimulating atmosphere.
D.G. learnt a lot about degenerate Whittaker models from a semester-long seminar in Tel Aviv university organized by Erez Lapid and David Soudry, and on geometry of nilpotent orbits from a spring school at the Weizmann Institute organized by Anthony Joseph and Anna Melnikov.
D.G. was partially supported by ERC StG grant 637912, ISF grant 756/12 and a Minerva foundation grant.
Part of the work on this paper was done during the visit of S. Sahi to Israel in summer 2014. This visit was partially funded by the ERC grant 291612.
Appendix A Schwartz induction and the proof of Lemma 2.3.4
We start with the following lemmas from functional analysis.
Lemma A.0.1 [Reference TrevesTre67, Theorem 50.1 and Proposition 50.1].
Let
![]() $V$
and
$V$
and
![]() $W$
be Hausdorff locally convex complete topological vector spaces. Suppose that
$W$
be Hausdorff locally convex complete topological vector spaces. Suppose that
![]() $V$
is a nuclear space. Then the projective and the injective topologies on
$V$
is a nuclear space. Then the projective and the injective topologies on
![]() $V\otimes W$
agree, and we will denote the completion with respect to these topologies by
$V\otimes W$
agree, and we will denote the completion with respect to these topologies by
![]() $V\,\widehat{\otimes }\,W$
. Moreover:
$V\,\widehat{\otimes }\,W$
. Moreover:
-
(i)
 $V^{\ast }$
is nuclear;
$V^{\ast }$
is nuclear; -
(ii) if
 $W$
is nuclear as well, then
$W$
is nuclear as well, then
 $V\,\widehat{\otimes }\,W$
is nuclear;
$V\,\widehat{\otimes }\,W$
is nuclear; -
(iii) if
 $U\subset V$
is a closed subspace, then both
$U\subset V$
is a closed subspace, then both
 $U$
and
$U$
and
 $V/U$
are nuclear.
$V/U$
are nuclear.
Here,
![]() $V^{\ast }$
and
$V^{\ast }$
and
![]() $W^{\ast }$
denote the strong dual.
$W^{\ast }$
denote the strong dual.
Lemma A.0.2 [Reference TrevesTre67, formulas (50.18) and (50.19)].
Let
![]() $V$
and
$V$
and
![]() $W$
be Fréchet spaces. Suppose that
$W$
be Fréchet spaces. Suppose that
![]() $V$
is a nuclear space. Then:
$V$
is a nuclear space. Then:
-
(i)
 $(V\,\widehat{\otimes }\,W)^{\ast }\cong V^{\ast }\,\widehat{\otimes }\,W^{\ast }$
;
$(V\,\widehat{\otimes }\,W)^{\ast }\cong V^{\ast }\,\widehat{\otimes }\,W^{\ast }$
; -
(ii)
 $L(V,W)\cong V^{\ast }\,\widehat{\otimes }\,W$
.
$L(V,W)\cong V^{\ast }\,\widehat{\otimes }\,W$
.
Here,
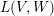 $L(V,W)$
denotes the space of all continuous linear maps from
$L(V,W)$
denotes the space of all continuous linear maps from
![]() $V$
to
$V$
to
![]() $W$
, endowed with the compact-open topology.
$W$
, endowed with the compact-open topology.
Lemma A.0.3 [Reference du ClouxdCl91, Corollary 1.2.5 and Proposition 1.2.6].
-
(i) Let
 $G$
be an affine real algebraic group. Then
$G$
be an affine real algebraic group. Then
 ${\mathcal{S}}(G)$
is a nuclear Fréchet space and for any smooth Fréchet representation
${\mathcal{S}}(G)$
is a nuclear Fréchet space and for any smooth Fréchet representation
 $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
 $G$
of moderate growth, we have a natural isomorphism
$G$
of moderate growth, we have a natural isomorphism  $$\begin{eqnarray}{\mathcal{S}}(G)\,\widehat{\otimes }\,\unicode[STIX]{x1D70B}\cong {\mathcal{S}}(G,\unicode[STIX]{x1D70B}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}(G)\,\widehat{\otimes }\,\unicode[STIX]{x1D70B}\cong {\mathcal{S}}(G,\unicode[STIX]{x1D70B}).\end{eqnarray}$$
-
(ii) For two smooth affine semi-algebraic varieties
 $M,N$
we have
$M,N$
we have
 ${\mathcal{S}}(M)\,\widehat{\otimes }\,{\mathcal{S}}(N)\cong {\mathcal{S}}(M\times N)$
.
${\mathcal{S}}(M)\,\widehat{\otimes }\,{\mathcal{S}}(N)\cong {\mathcal{S}}(M\times N)$
.
Lemma A.0.4. Given
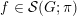 $f\in {\mathcal{S}}(G;\unicode[STIX]{x1D70B})$
and
$f\in {\mathcal{S}}(G;\unicode[STIX]{x1D70B})$
and
![]() $x$
,
$x$
,
![]() $g\in G$
, we define
$g\in G$
, we define
 $$\begin{eqnarray}\displaystyle & \displaystyle (R(g)f)(x)=f(xg),\quad (R\unicode[STIX]{x1D70B}(g)f)(x)=\unicode[STIX]{x1D70B}(g)f(xg), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (L(g)f)(x)=f(g^{-1}x),\quad (L\unicode[STIX]{x1D70B}(g)f)(x)=\unicode[STIX]{x1D70B}(g)f(g^{-1}x). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (R(g)f)(x)=f(xg),\quad (R\unicode[STIX]{x1D70B}(g)f)(x)=\unicode[STIX]{x1D70B}(g)f(xg), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (L(g)f)(x)=f(g^{-1}x),\quad (L\unicode[STIX]{x1D70B}(g)f)(x)=\unicode[STIX]{x1D70B}(g)f(g^{-1}x). & \displaystyle \nonumber\end{eqnarray}$$
Then, all of the induced
![]() $G$
-module structures on
$G$
-module structures on
![]() ${\mathcal{S}}(G;\unicode[STIX]{x1D70B})$
are isomorphic.
${\mathcal{S}}(G;\unicode[STIX]{x1D70B})$
are isomorphic.
Proof. Given
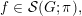 $f\in {\mathcal{S}}(G;\unicode[STIX]{x1D70B}),$
let
$f\in {\mathcal{S}}(G;\unicode[STIX]{x1D70B}),$
let
 $$\begin{eqnarray}\widetilde{f}(x)=f(x^{-1})\quad \text{for all}~x\in G.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{f}(x)=f(x^{-1})\quad \text{for all}~x\in G.\end{eqnarray}$$
Then
 $$\begin{eqnarray}\displaystyle (\widetilde{R(g)f})(x)=(R(g)f)(x^{-1})=f(x^{-1}g)=\widetilde{f}(g^{-1}x)=(L(g)\widetilde{f})(x). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\widetilde{R(g)f})(x)=(R(g)f)(x^{-1})=f(x^{-1}g)=\widetilde{f}(g^{-1}x)=(L(g)\widetilde{f})(x). & & \displaystyle \nonumber\end{eqnarray}$$
It is clear, then, that the map
![]() $f\mapsto \widetilde{f}$
defines a
$f\mapsto \widetilde{f}$
defines a
![]() $G$
-intertwining isomorphism between
$G$
-intertwining isomorphism between
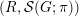 $(R,{\mathcal{S}}(G;\unicode[STIX]{x1D70B}))$
and
$(R,{\mathcal{S}}(G;\unicode[STIX]{x1D70B}))$
and
 $(L,{\mathcal{S}}(G;\unicode[STIX]{x1D70B}))$
. Similarly, given
$(L,{\mathcal{S}}(G;\unicode[STIX]{x1D70B}))$
. Similarly, given
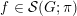 $f\in {\mathcal{S}}(G;\unicode[STIX]{x1D70B})$
, we set
$f\in {\mathcal{S}}(G;\unicode[STIX]{x1D70B})$
, we set
 $$\begin{eqnarray}\widehat{f}(x)=\unicode[STIX]{x1D70B}(x)f(x)\quad \text{for all}~x\in G.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{f}(x)=\unicode[STIX]{x1D70B}(x)f(x)\quad \text{for all}~x\in G.\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D70F}$
is of moderate growth,
$\unicode[STIX]{x1D70F}$
is of moderate growth,
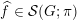 $\widehat{f}\in {\mathcal{S}}(G;\unicode[STIX]{x1D70B})$
and
$\widehat{f}\in {\mathcal{S}}(G;\unicode[STIX]{x1D70B})$
and
 $$\begin{eqnarray}\displaystyle \widehat{R\unicode[STIX]{x1D70B}(g)f}(x)=\unicode[STIX]{x1D70B}(x)(R\unicode[STIX]{x1D70B}(g)f)(x)=\unicode[STIX]{x1D70B}(x)\unicode[STIX]{x1D70B}(g)f(xg)=\widehat{f}(xg)=(R(g)\widehat{f})(x), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{R\unicode[STIX]{x1D70B}(g)f}(x)=\unicode[STIX]{x1D70B}(x)(R\unicode[STIX]{x1D70B}(g)f)(x)=\unicode[STIX]{x1D70B}(x)\unicode[STIX]{x1D70B}(g)f(xg)=\widehat{f}(xg)=(R(g)\widehat{f})(x), & & \displaystyle \nonumber\end{eqnarray}$$
that is, the map
![]() $f\mapsto \widehat{f}$
defines a
$f\mapsto \widehat{f}$
defines a
![]() $G$
-intertwining isomorphism between the spaces
$G$
-intertwining isomorphism between the spaces
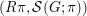 $(R\unicode[STIX]{x1D70B},{\mathcal{S}}(G;\unicode[STIX]{x1D70B}))$
and
$(R\unicode[STIX]{x1D70B},{\mathcal{S}}(G;\unicode[STIX]{x1D70B}))$
and
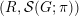 $(R,{\mathcal{S}}(G;\unicode[STIX]{x1D70B}))$
. The other isomorphisms are similar.◻
$(R,{\mathcal{S}}(G;\unicode[STIX]{x1D70B}))$
. The other isomorphisms are similar.◻
Corollary A.0.5. Under any of the above
![]() $G$
-module structures,
$G$
-module structures,
 $$\begin{eqnarray}{\mathcal{S}}(G;\unicode[STIX]{x1D70B})_{G}\cong \unicode[STIX]{x1D70B},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}(G;\unicode[STIX]{x1D70B})_{G}\cong \unicode[STIX]{x1D70B},\end{eqnarray}$$
where
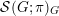 ${\mathcal{S}}(G;\unicode[STIX]{x1D70B})_{G}$
is the space of
${\mathcal{S}}(G;\unicode[STIX]{x1D70B})_{G}$
is the space of
![]() $G$
-coinvariants, i.e. the quotient of
$G$
-coinvariants, i.e. the quotient of
![]() ${\mathcal{S}}(G;\unicode[STIX]{x1D70B})$
by the joint kernel of all
${\mathcal{S}}(G;\unicode[STIX]{x1D70B})$
by the joint kernel of all
![]() $G$
-invariant functionals.
$G$
-invariant functionals.
Lemma A.0.6. We have
 $$\begin{eqnarray}\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})\cong ({\mathcal{S}}(G,\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})_{H}.\end{eqnarray}$$
$$\begin{eqnarray}\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})\cong ({\mathcal{S}}(G,\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})_{H}.\end{eqnarray}$$
Proof. Let
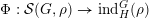 $\unicode[STIX]{x1D6F7}:{\mathcal{S}}(G,\unicode[STIX]{x1D70C})\rightarrow \text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})$
denote the surjection that defines
$\unicode[STIX]{x1D6F7}:{\mathcal{S}}(G,\unicode[STIX]{x1D70C})\rightarrow \text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})$
denote the surjection that defines
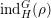 $\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})$
, see Definition 2.3.1. Observe that for all
$\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})$
, see Definition 2.3.1. Observe that for all
![]() $\tilde{h}\in H$
,
$\tilde{h}\in H$
,
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6F7}(R\unicode[STIX]{x1D70C}(\tilde{h})f))(g)=\int _{H}\unicode[STIX]{x1D70C}(h)(R\unicode[STIX]{x1D70C}(\tilde{h}))f(gh)\,dh=\int _{H}\unicode[STIX]{x1D70C}(h)^{}\unicode[STIX]{x1D70C}(\tilde{h})f(gh\tilde{h})\,dh=\unicode[STIX]{x1D6E5}_{H}^{-1}(\tilde{h})\unicode[STIX]{x1D6F7}(f)(g). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6F7}(R\unicode[STIX]{x1D70C}(\tilde{h})f))(g)=\int _{H}\unicode[STIX]{x1D70C}(h)(R\unicode[STIX]{x1D70C}(\tilde{h}))f(gh)\,dh=\int _{H}\unicode[STIX]{x1D70C}(h)^{}\unicode[STIX]{x1D70C}(\tilde{h})f(gh\tilde{h})\,dh=\unicode[STIX]{x1D6E5}_{H}^{-1}(\tilde{h})\unicode[STIX]{x1D6F7}(f)(g). & & \displaystyle \nonumber\end{eqnarray}$$
Hence, the map
![]() $\unicode[STIX]{x1D6F7}$
defines an
$\unicode[STIX]{x1D6F7}$
defines an
![]() $H$
-invariant operator between
$H$
-invariant operator between
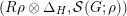 $(R\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D6E5}_{H},{\mathcal{S}}(G;\unicode[STIX]{x1D70C}))$
and
$(R\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D6E5}_{H},{\mathcal{S}}(G;\unicode[STIX]{x1D70C}))$
and
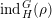 $\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})$
. Since this operator is surjective, it should factor through a surjective map
$\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})$
. Since this operator is surjective, it should factor through a surjective map
 $$\begin{eqnarray}({\mathcal{S}}(G;\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})_{H}{\twoheadrightarrow}\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C}).\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{S}}(G;\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})_{H}{\twoheadrightarrow}\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C}).\end{eqnarray}$$
We want to show that this map is injective. Let us fix
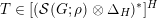 $T\in [({\mathcal{S}}(G;\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})^{\ast }]^{H}$
. Now according to [Reference du ClouxdCl91, Lemma 2.2.5], there exists a semi-algebraic open cover
$T\in [({\mathcal{S}}(G;\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})^{\ast }]^{H}$
. Now according to [Reference du ClouxdCl91, Lemma 2.2.5], there exists a semi-algebraic open cover
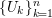 $\{U_{k}\}_{k=1}^{n}$
of
$\{U_{k}\}_{k=1}^{n}$
of
![]() $G/H$
and a tempered partition of unity
$G/H$
and a tempered partition of unity
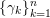 $\{\unicode[STIX]{x1D6FE}_{k}\}_{k=1}^{n}$
subordinated to
$\{\unicode[STIX]{x1D6FE}_{k}\}_{k=1}^{n}$
subordinated to
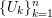 $\{U_{k}\}_{k=1}^{n}$
such that
$\{U_{k}\}_{k=1}^{n}$
such that
 $$\begin{eqnarray}p^{-1}(U_{k})\cong U_{k}\times H,\end{eqnarray}$$
$$\begin{eqnarray}p^{-1}(U_{k})\cong U_{k}\times H,\end{eqnarray}$$
where
 $p:G\longrightarrow G/H$
is the natural projection. Using the above equation, we can define a partition of unity
$p:G\longrightarrow G/H$
is the natural projection. Using the above equation, we can define a partition of unity
![]() $\{\unicode[STIX]{x1D702}_{k}\}_{k=1}^{n}$
subordinated to the open cover
$\{\unicode[STIX]{x1D702}_{k}\}_{k=1}^{n}$
subordinated to the open cover
 $\{p^{-1}(U_{k})\}$
consisting of
$\{p^{-1}(U_{k})\}$
consisting of
![]() $H$
-invariant functions. Furthermore, given
$H$
-invariant functions. Furthermore, given
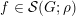 $f\in {\mathcal{S}}(G;\unicode[STIX]{x1D70C})$
,
$f\in {\mathcal{S}}(G;\unicode[STIX]{x1D70C})$
,
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}_{k}f)=\unicode[STIX]{x1D6FE}_{k}\unicode[STIX]{x1D6F7}(f),\quad k=1,\ldots ,n.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}_{k}f)=\unicode[STIX]{x1D6FE}_{k}\unicode[STIX]{x1D6F7}(f),\quad k=1,\ldots ,n.\end{eqnarray}$$
Therefore, we have a decomposition
 $$\begin{eqnarray}T=\mathop{\sum }_{k=1}^{n}\unicode[STIX]{x1D702}_{k}T\end{eqnarray}$$
$$\begin{eqnarray}T=\mathop{\sum }_{k=1}^{n}\unicode[STIX]{x1D702}_{k}T\end{eqnarray}$$
and we can identify each
![]() $\unicode[STIX]{x1D702}_{k}T$
with an element of
$\unicode[STIX]{x1D702}_{k}T$
with an element of
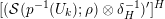 $[({\mathcal{S}}(p^{-1}(U_{k});\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6FF}_{H}^{-1})^{\prime }]^{H}$
. According to (A.2),
$[({\mathcal{S}}(p^{-1}(U_{k});\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6FF}_{H}^{-1})^{\prime }]^{H}$
. According to (A.2),
 $$\begin{eqnarray}{\mathcal{S}}(p^{-1}(U_{k}))\cong {\mathcal{S}}(H)\widehat{\otimes }{\mathcal{S}}(U_{k})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}(p^{-1}(U_{k}))\cong {\mathcal{S}}(H)\widehat{\otimes }{\mathcal{S}}(U_{k})\end{eqnarray}$$
and, hence, according to Corollary A.0.5
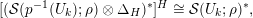 $[({\mathcal{S}}(p^{-1}(U_{k});\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})^{\ast }]^{H}\cong {\mathcal{S}}(U_{k};\unicode[STIX]{x1D70C})^{\ast },$
that is, for all
$[({\mathcal{S}}(p^{-1}(U_{k});\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})^{\ast }]^{H}\cong {\mathcal{S}}(U_{k};\unicode[STIX]{x1D70C})^{\ast },$
that is, for all
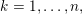 $k=1,\ldots ,n,$
there exists
$k=1,\ldots ,n,$
there exists
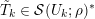 $\tilde{T}_{k}\in {\mathcal{S}}(U_{k};\unicode[STIX]{x1D70C})^{\ast }$
such that
$\tilde{T}_{k}\in {\mathcal{S}}(U_{k};\unicode[STIX]{x1D70C})^{\ast }$
such that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{k}T(f)=\tilde{T}_{k}(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}_{k}f))=\tilde{T}_{k}(\unicode[STIX]{x1D6FE}_{k}\unicode[STIX]{x1D6F7}(f))=(\unicode[STIX]{x1D6FE}_{k}T_{k}\circ \unicode[STIX]{x1D6F7})(f). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{k}T(f)=\tilde{T}_{k}(\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}_{k}f))=\tilde{T}_{k}(\unicode[STIX]{x1D6FE}_{k}\unicode[STIX]{x1D6F7}(f))=(\unicode[STIX]{x1D6FE}_{k}T_{k}\circ \unicode[STIX]{x1D6F7})(f). & & \displaystyle \nonumber\end{eqnarray}$$
But we can see
![]() $\unicode[STIX]{x1D6FE}_{k}T_{k}$
as an element of
$\unicode[STIX]{x1D6FE}_{k}T_{k}$
as an element of
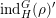 $\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})^{\prime }$
. Therefore, if we set
$\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})^{\prime }$
. Therefore, if we set
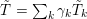 $\tilde{T}=\sum _{k}\unicode[STIX]{x1D6FE}_{k}\tilde{T}_{k}$
, then
$\tilde{T}=\sum _{k}\unicode[STIX]{x1D6FE}_{k}\tilde{T}_{k}$
, then
 $$\begin{eqnarray}T=\mathop{\sum }_{k}\unicode[STIX]{x1D702}_{k}T=\mathop{\sum }_{k}\unicode[STIX]{x1D6FE}_{k}\tilde{T}_{k}\circ \unicode[STIX]{x1D6F7}=\tilde{T}\circ \unicode[STIX]{x1D6F7}.\end{eqnarray}$$
$$\begin{eqnarray}T=\mathop{\sum }_{k}\unicode[STIX]{x1D702}_{k}T=\mathop{\sum }_{k}\unicode[STIX]{x1D6FE}_{k}\tilde{T}_{k}\circ \unicode[STIX]{x1D6F7}=\tilde{T}\circ \unicode[STIX]{x1D6F7}.\end{eqnarray}$$
We have thus shown that any element of
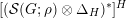 $[({\mathcal{S}}(G;\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})^{\ast }]^{H}$
factors through
$[({\mathcal{S}}(G;\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})^{\ast }]^{H}$
factors through
 $\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})^{\ast }$
which proves the injectivity of the map (A.1).◻
$\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C})^{\ast }$
which proves the injectivity of the map (A.1).◻
Proof of Lemma 2.3.4.
We have
 $$\begin{eqnarray}\displaystyle \text{Hom}_{G}(\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C}),\unicode[STIX]{x1D70B}^{\ast }) & \cong & \displaystyle ((({\mathcal{S}}(G,\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})^{\ast })^{H}\,\widehat{\otimes }\,\unicode[STIX]{x1D70B}^{\ast })^{G}\cong \text{Hom}_{G\times H}({\mathcal{S}}(G,\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H},\unicode[STIX]{x1D70B}^{\ast })\nonumber\\ \displaystyle & \cong & \displaystyle \text{Hom}_{G\times H}({\mathcal{S}}(G,\unicode[STIX]{x1D70C})\,\widehat{\otimes }\,\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D6E5}_{H},\mathbb{C})\cong \text{Hom}_{G\times H}(\unicode[STIX]{x1D70C}\,\widehat{\otimes }\,{\mathcal{S}}(G,\unicode[STIX]{x1D70B})\otimes \unicode[STIX]{x1D6E5}_{H},\mathbb{C}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Hom}_{G}(\text{ind}_{H}^{G}(\unicode[STIX]{x1D70C}),\unicode[STIX]{x1D70B}^{\ast }) & \cong & \displaystyle ((({\mathcal{S}}(G,\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H})^{\ast })^{H}\,\widehat{\otimes }\,\unicode[STIX]{x1D70B}^{\ast })^{G}\cong \text{Hom}_{G\times H}({\mathcal{S}}(G,\unicode[STIX]{x1D70C})\otimes \unicode[STIX]{x1D6E5}_{H},\unicode[STIX]{x1D70B}^{\ast })\nonumber\\ \displaystyle & \cong & \displaystyle \text{Hom}_{G\times H}({\mathcal{S}}(G,\unicode[STIX]{x1D70C})\,\widehat{\otimes }\,\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D6E5}_{H},\mathbb{C})\cong \text{Hom}_{G\times H}(\unicode[STIX]{x1D70C}\,\widehat{\otimes }\,{\mathcal{S}}(G,\unicode[STIX]{x1D70B})\otimes \unicode[STIX]{x1D6E5}_{H},\mathbb{C}).\nonumber\end{eqnarray}$$
Here,
![]() $G$
acts on
$G$
acts on
![]() ${\mathcal{S}}(G,\unicode[STIX]{x1D70B})$
by
${\mathcal{S}}(G,\unicode[STIX]{x1D70B})$
by
![]() $L\unicode[STIX]{x1D70B}$
, while
$L\unicode[STIX]{x1D70B}$
, while
![]() $H$
acts diagonally: on
$H$
acts diagonally: on
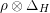 $\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D6E5}_{H}$
and on
$\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D6E5}_{H}$
and on
![]() ${\mathcal{S}}(G,\unicode[STIX]{x1D70B})$
by
${\mathcal{S}}(G,\unicode[STIX]{x1D70B})$
by
![]() $R$
. This action is isomorphic to an action in which
$R$
. This action is isomorphic to an action in which
![]() $G$
acts on
$G$
acts on
![]() ${\mathcal{S}}(G,\unicode[STIX]{x1D70B})$
by
${\mathcal{S}}(G,\unicode[STIX]{x1D70B})$
by
![]() $L$
and
$L$
and
![]() $H$
by
$H$
by
![]() $R\unicode[STIX]{x1D70B}$
. Under this action we have
$R\unicode[STIX]{x1D70B}$
. Under this action we have
 $$\begin{eqnarray}\text{Hom}_{G\times H}(\unicode[STIX]{x1D70C}\,\widehat{\otimes }\,{\mathcal{S}}(G,\unicode[STIX]{x1D70B})\otimes \unicode[STIX]{x1D6E5}_{H},\mathbb{C})\cong (({\mathcal{S}}^{\ast }(G))^{G}\,\widehat{\otimes }\,\unicode[STIX]{x1D70B}^{\ast }\,\widehat{\otimes }\,\unicode[STIX]{x1D70C}^{\ast }\otimes \unicode[STIX]{x1D6E5}_{H}^{-1})^{H}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{G\times H}(\unicode[STIX]{x1D70C}\,\widehat{\otimes }\,{\mathcal{S}}(G,\unicode[STIX]{x1D70B})\otimes \unicode[STIX]{x1D6E5}_{H},\mathbb{C})\cong (({\mathcal{S}}^{\ast }(G))^{G}\,\widehat{\otimes }\,\unicode[STIX]{x1D70B}^{\ast }\,\widehat{\otimes }\,\unicode[STIX]{x1D70C}^{\ast }\otimes \unicode[STIX]{x1D6E5}_{H}^{-1})^{H}.\end{eqnarray}$$
Since all left
![]() $G$
-invariant distributions on
$G$
-invariant distributions on
![]() $G$
are proportional and right
$G$
are proportional and right
![]() $\unicode[STIX]{x1D6E5}_{G}$
-equivariant, the latter space is isomorphic to
$\unicode[STIX]{x1D6E5}_{G}$
-equivariant, the latter space is isomorphic to
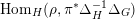 $\text{Hom}_{H}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E5}_{H}^{-1}\unicode[STIX]{x1D6E5}_{G})$
.◻
$\text{Hom}_{H}(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6E5}_{H}^{-1}\unicode[STIX]{x1D6E5}_{G})$
.◻