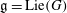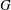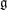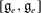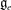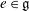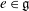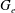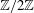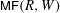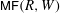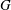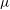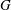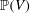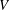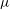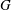Research Article
Stable maps and stable quotients
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1457-1481
-
- Article
-
- You have access
- Export citation
Corrigendum
Corrigendum: Filtering free resolutions
- Part of:
-
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1482-1484
-
- Article
-
- You have access
- Export citation
Research Article
Derived subalgebras of centralisers and finite
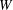 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}W$-algebras
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}W$-algebras
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2014, pp. 1485-1548
-
- Article
-
- You have access
- Export citation
Matrix factorizations via Koszul duality
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1549-1578
-
- Article
-
- You have access
- Export citation
Random walks on projective spaces
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1579-1606
-
- Article
-
- You have access
- Export citation
Normal crossing properties of complex hypersurfaces via logarithmic residues
- Part of:
-
- Published online by Cambridge University Press:
- 25 June 2014, pp. 1607-1622
-
- Article
-
- You have access
- Export citation
Separability of embedded surfaces in 3-manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1623-1630
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
COM volume 150 Issue 9 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 September 2014, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
COM volume 150 Issue 9 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 September 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation