Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Friedl, Stefan
Silver, Daniel S.
and
Williams, Susan G.
2015.
Splittings of knot groups.
Mathematische Annalen,
Vol. 362,
Issue. 1-2,
p.
401.
Derbez, Pierre
Liu, Yi
and
Wang, Shicheng
2015.
Chern–Simons theory, surface separability, and volumes of 3-manifolds.
Journal of Topology,
Vol. 8,
Issue. 4,
p.
933.
Derbez, Pierre
Liu, Yi
Sun, Hongbin
and
Wang, Shicheng
2017.
Positive simplicial volume implies virtually positive Seifert volume for 3–manifolds.
Geometry & Topology,
Vol. 21,
Issue. 5,
p.
3159.
Boileau, Michel
and
Friedl, Stefan
2018.
Epimorphisms of 3-manifold groups.
The Quarterly Journal of Mathematics,
Vol. 69,
Issue. 3,
p.
931.
Wilkes, Gareth
2019.
Relative cohomology theory for profinite groups.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 4,
p.
1617.
Nguyen, Hoang Thanh
2019.
Distortion of surfaces in 3‐manifolds.
Journal of Topology,
Vol. 12,
Issue. 4,
p.
1115.
Hruska, Christopher
and
Nguyen, Hoang
2019.
Distortion of surfaces in graph manifolds.
Algebraic & Geometric Topology,
Vol. 19,
Issue. 1,
p.
363.
Sun, Hongbin
2019.
Non-LERFness of arithmetic hyperbolic manifold groups and mixed 3-manifold groups.
Duke Mathematical Journal,
Vol. 168,
Issue. 4,
Nguyen, Hoang
and
Sun, Hongbin
2020.
Subgroup distortion of 3-manifold groups.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 9,
p.
6683.
Boileau, Michel
2020.
Around 3-manifold groups.
Winter Braids Lecture Notes,
Vol. 5,
Issue. ,
p.
1.
Sun, Hongbin
2020.
A characterization on separable subgroups of 3‐manifold groups.
Journal of Topology,
Vol. 13,
Issue. 1,
p.
187.
Jaikin-Zapirain, Andrei
2020.
Recognition of being fibered for compact 3–manifolds.
Geometry & Topology,
Vol. 24,
Issue. 1,
p.
409.
Nguyen, Hoang Thanh
Tran, Hung Cong
and
Yang, Wenyuan
2021.
Quasiconvexity in 3-manifold groups.
Mathematische Annalen,
Vol. 381,
Issue. 1-2,
p.
405.
Hara, Takashi
and
Kitayama, Takahiro
2021.
Character varieties of higher dimensional representations and splittings of 3-manifolds.
Geometriae Dedicata,
Vol. 213,
Issue. 1,
p.
433.
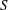 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}S$ is a properly embedded
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}S$ is a properly embedded 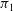 $\pi _1$-injective surface in a compact 3-manifold
$\pi _1$-injective surface in a compact 3-manifold 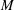 $M$, then
$M$, then 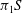 $\pi _1S$ is separable in
$\pi _1S$ is separable in 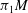 $\pi _1M$.
$\pi _1M$.



