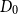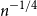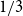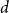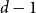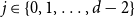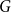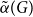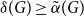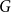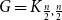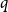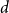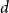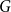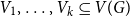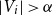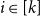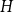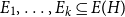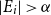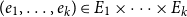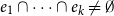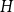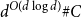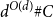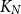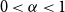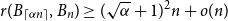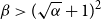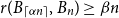FirstView articles
Paper
Counting spanning subgraphs in dense hypergraphs
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-13
-
- Article
- Export citation
A generalisation of Varnavides’s theorem
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2024, pp. 1-5
-
- Article
- Export citation
Noise sensitivity of the minimum spanning tree of the complete graph
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rainbow Hamiltonicity in uniformly coloured perturbed digraphs
- Part of:
-
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximum chordal subgraphs of random graphs
- Part of:
-
- Published online by Cambridge University Press:
- 03 May 2024, pp. 1-13
-
- Article
- Export citation
Central limit theorem for components in meandric systems through high moments
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turán problems in pseudorandom graphs
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Behaviour of the minimum degree throughout the
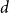 ${\textit{d}}$-process
${\textit{d}}$-process
- Part of:
-
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalization of Bondy’s pancyclicity theorem
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The distribution of the maximum protection number in simply generated trees
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algorithms for the ferromagnetic Potts model on expanders
- Part of:
-
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Antidirected subgraphs of oriented graphs
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
Large monochromatic components in expansive hypergraphs
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp bounds for a discrete John’s theorem
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-3
-
- Article
- Export citation
Small subsets with large sumset: Beyond the Cauchy–Davenport bound
- Part of:
-
- Published online by Cambridge University Press:
- 21 February 2024, pp. 1-21
-
- Article
- Export citation
On a conjecture of Conlon, Fox, and Wigderson
- Part of:
-
- Published online by Cambridge University Press:
- 16 February 2024, pp. 1-14
-
- Article
- Export citation