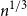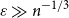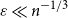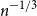1. Introduction
The minimum spanning tree (MST) of a weighted graph is a classical object in discrete mathematics, whose research goes back to Borůvka’s Algorithm from 1926 (see [Reference Nešetřil, Milková and Nešetřilová22]). Denote by
![]() ${\mathbb{M}}_n$
the MST of the
${\mathbb{M}}_n$
the MST of the
![]() $n$
-vertex complete graph
$n$
-vertex complete graph
![]() $K_n$
assigned with independent
$K_n$
assigned with independent
![]() $\mathrm{U}[0,1]$
-distributed edge weights
$\mathrm{U}[0,1]$
-distributed edge weights
![]() $W_n=(w_e)_{e\in K_n}$
. Frieze [Reference Frieze10] famously showed that the expected total weight of
$W_n=(w_e)_{e\in K_n}$
. Frieze [Reference Frieze10] famously showed that the expected total weight of
![]() ${\mathbb{M}}_n$
converges to
${\mathbb{M}}_n$
converges to
![]() $\zeta (3)$
, initiating an extensive study of the distribution of the total weight (e.g., [Reference Janson14, Reference Janson and Wästlund16]). From a purely graph-theoretic perspective, a decade old fundamental work on the metric structure of
$\zeta (3)$
, initiating an extensive study of the distribution of the total weight (e.g., [Reference Janson14, Reference Janson and Wästlund16]). From a purely graph-theoretic perspective, a decade old fundamental work on the metric structure of
![]() ${\mathbb{M}}_n$
by Addario-Berry, Broutin, Goldschmidt, and Miermont [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4], which plays a key role in this paper, discovered the existence of a scaling limit of
${\mathbb{M}}_n$
by Addario-Berry, Broutin, Goldschmidt, and Miermont [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4], which plays a key role in this paper, discovered the existence of a scaling limit of
![]() ${\mathbb{M}}_n$
as a measured metric space. An explicit construction of the limit was recently obtained in ref. [Reference Broutin and Marckert9]. In addition, the local weak limit of
${\mathbb{M}}_n$
as a measured metric space. An explicit construction of the limit was recently obtained in ref. [Reference Broutin and Marckert9]. In addition, the local weak limit of
![]() ${\mathbb{M}}_n$
was studied in refs. [Reference Addario-Berry1, Reference Angel and Sénizergues6].
${\mathbb{M}}_n$
was studied in refs. [Reference Addario-Berry1, Reference Angel and Sénizergues6].
The notion of noise sensitivity of Boolean functions, that was introduced by Benjamini, Kalai, and Schramm in ref. [Reference Benjamini, Kalai and Schramm7], can be directly applied to the random MST. Namely, let
![]() $\varepsilon =\varepsilon _n$
be a noise parameter, and
$\varepsilon =\varepsilon _n$
be a noise parameter, and
![]() $W_n^\varepsilon =(w^{\varepsilon }_e)_{e\in K_n}$
be obtained from
$W_n^\varepsilon =(w^{\varepsilon }_e)_{e\in K_n}$
be obtained from
![]() $W_n$
by resampling each
$W_n$
by resampling each
![]() $w_e$
independently with probability
$w_e$
independently with probability
![]() $\varepsilon$
. The MST of
$\varepsilon$
. The MST of
![]() $K_n$
with respect to the new weights
$K_n$
with respect to the new weights
![]() $W_n^\varepsilon$
is denoted by
$W_n^\varepsilon$
is denoted by
![]() ${\mathbb{M}}_n^{\varepsilon }$
. Suppose
${\mathbb{M}}_n^{\varepsilon }$
. Suppose
![]() $f_n$
is a sequence of Boolean functions defined on
$f_n$
is a sequence of Boolean functions defined on
![]() $n$
-vertex trees, such that
$n$
-vertex trees, such that
![]() $\mathbb{E}[f_n({\mathbb{M}}_n)]$
is bounded away from
$\mathbb{E}[f_n({\mathbb{M}}_n)]$
is bounded away from
![]() $0$
and
$0$
and
![]() $1$
as
$1$
as
![]() $n\to \infty$
. We say that the sequence
$n\to \infty$
. We say that the sequence
![]() $f_n$
is
$f_n$
is
![]() $\varepsilon$
-noise sensitive (resp. stable) if
$\varepsilon$
-noise sensitive (resp. stable) if
![]() $\mathrm{Cov}(f_n({\mathbb{M}}_n),f_n({\mathbb{M}}_n^{\varepsilon }))\to 0$
(resp.
$\mathrm{Cov}(f_n({\mathbb{M}}_n),f_n({\mathbb{M}}_n^{\varepsilon }))\to 0$
(resp.
![]() $1$
) as
$1$
) as
![]() $n\to \infty$
. This paper deals with the noise sensitivity and stability of (functions that depend on) the scaled measured metric structure of
$n\to \infty$
. This paper deals with the noise sensitivity and stability of (functions that depend on) the scaled measured metric structure of
![]() ${\mathbb{M}}_n$
.
${\mathbb{M}}_n$
.
1.1 The metric structure of the random MST
The tree
![]() ${\mathbb{M}}_n$
is closely related to the Erdős-Rényi random graph. Kruskal’s algorithm [Reference Kruskal17] computes the tree
${\mathbb{M}}_n$
is closely related to the Erdős-Rényi random graph. Kruskal’s algorithm [Reference Kruskal17] computes the tree
![]() ${\mathbb{M}}_n$
by starting from an empty
${\mathbb{M}}_n$
by starting from an empty
![]() $n$
-vertex graph and adding edges according to their (uniformly random) increasing weight order, unless the addition of an edge forms a cycle. Therefore, the minimum spanning forest (MSF)
$n$
-vertex graph and adding edges according to their (uniformly random) increasing weight order, unless the addition of an edge forms a cycle. Therefore, the minimum spanning forest (MSF)
![]() ${\mathbb{M}}(n,p)$
of the random graph
${\mathbb{M}}(n,p)$
of the random graph
![]() $\mathbb G(n,p)\;:\!=\;\{e\in K_n\;:\;w_e\le p\}$
(endowed with the random weights from
$\mathbb G(n,p)\;:\!=\;\{e\in K_n\;:\;w_e\le p\}$
(endowed with the random weights from
![]() $W_n$
) is a subgraph of
$W_n$
) is a subgraph of
![]() ${\mathbb{M}}_n$
. Indeed,
${\mathbb{M}}_n$
. Indeed,
![]() ${\mathbb{M}}(n,p)$
is one of the forests en route
${\mathbb{M}}(n,p)$
is one of the forests en route
![]() ${\mathbb{M}}_n$
in Kruskal’s algorithm. In addition,
${\mathbb{M}}_n$
in Kruskal’s algorithm. In addition,
![]() ${\mathbb{M}}(n,p)$
can be obtained from
${\mathbb{M}}(n,p)$
can be obtained from
![]() $\mathbb{G}(n,p)$
using a cycle-breaking algorithm, i.e., by repeatedly deleting the heaviest edge participating in a cycle until the graph becomes acyclic (see section 2).
$\mathbb{G}(n,p)$
using a cycle-breaking algorithm, i.e., by repeatedly deleting the heaviest edge participating in a cycle until the graph becomes acyclic (see section 2).
Fix
![]() $\lambda \in{\mathbb{R}}$
and let
$\lambda \in{\mathbb{R}}$
and let
![]() $p(n,\lambda )=1/n + \lambda/n^{4/3}$
. We denote the critical random graph
$p(n,\lambda )=1/n + \lambda/n^{4/3}$
. We denote the critical random graph
![]() $\mathbb{G}_{n,\lambda }\;:\!=\;\mathbb G(n,p(n,\lambda ))$
and its MSF
$\mathbb{G}_{n,\lambda }\;:\!=\;\mathbb G(n,p(n,\lambda ))$
and its MSF
![]() ${\mathbb{M}}_{n,\lambda }\;:\!=\;\mathbb M(n,p(n,\lambda ))$
. These graphs play a key role in the study of the MST. It is shown in ref. [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4] (in a sense we precisely specify below), that for a large constant
${\mathbb{M}}_{n,\lambda }\;:\!=\;\mathbb M(n,p(n,\lambda ))$
. These graphs play a key role in the study of the MST. It is shown in ref. [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4] (in a sense we precisely specify below), that for a large constant
![]() $\lambda$
, ‘most’ of the global metric structure of
$\lambda$
, ‘most’ of the global metric structure of
![]() ${\mathbb{M}}_n$
is present in its subgraph
${\mathbb{M}}_n$
is present in its subgraph
![]() ${\mathbb{M}}_{n,\lambda }$
. The size and structure of the connected components of
${\mathbb{M}}_{n,\lambda }$
. The size and structure of the connected components of
![]() $\mathbb{G}_{n,\lambda }$
have been studied extensively [Reference Luczak, Pittel and Wierman20]. In his work on multiplicative coalescence, Aldous [Reference Aldous5] determined the limit law of the random sequence of the sizes of the connected components of
$\mathbb{G}_{n,\lambda }$
have been studied extensively [Reference Luczak, Pittel and Wierman20]. In his work on multiplicative coalescence, Aldous [Reference Aldous5] determined the limit law of the random sequence of the sizes of the connected components of
![]() $\mathbb{G}_{n,\lambda }$
, given in decreasing order and rescaled by
$\mathbb{G}_{n,\lambda }$
, given in decreasing order and rescaled by
![]() $n^{-2/3}$
. The limit law is beautifully expressed via a reflected Brownian motion with a parabolic drift. A breakthrough result of Addario-Berry, Broutin and Goldschmidt [Reference Addario-Berry, Broutin and Goldschmidt2] discovered the scaling limit in Gromov–Hausdorff distance of the connected components of
$n^{-2/3}$
. The limit law is beautifully expressed via a reflected Brownian motion with a parabolic drift. A breakthrough result of Addario-Berry, Broutin and Goldschmidt [Reference Addario-Berry, Broutin and Goldschmidt2] discovered the scaling limit in Gromov–Hausdorff distance of the connected components of
![]() $\mathbb{G}_{n,\lambda }$
viewed as metric spaces.
$\mathbb{G}_{n,\lambda }$
viewed as metric spaces.
In ref. [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4], these authors and Miermont extended this result to measured metric spaces in the Gromov–Hausdorff–Prokhorov (GHP) distance. In addition, by applying a continuous cycle-breaking algorithm on the scaling limit of the components, they discovered the scaling limit of
![]() ${\mathbb{M}}_n$
. More formally, let
${\mathbb{M}}_n$
. More formally, let
![]() $\mathcal{M}$
be the space of isometry-equivalence classes of compact measured metric spaces endowed with the GHP distance. Denote by
$\mathcal{M}$
be the space of isometry-equivalence classes of compact measured metric spaces endowed with the GHP distance. Denote by
![]() $M_n\in \mathcal{M}$
the measured metric space obtained from
$M_n\in \mathcal{M}$
the measured metric space obtained from
![]() ${\mathbb{M}}_n$
by rescaling graph distances by
${\mathbb{M}}_n$
by rescaling graph distances by
![]() $n^{-1/3}$
and assigning a uniform measure on the vertices. The main theorem in ref. [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4] asserts that there exists a random compact measured metric space
$n^{-1/3}$
and assigning a uniform measure on the vertices. The main theorem in ref. [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4] asserts that there exists a random compact measured metric space
![]() $\mathscr{M}$
such that
$\mathscr{M}$
such that
![]() $M_n\xrightarrow{\,\mathrm{d}\,}\mathscr{M}$
in the space
$M_n\xrightarrow{\,\mathrm{d}\,}\mathscr{M}$
in the space
![]() $(\mathcal{M},d_{\textrm{GHP}})$
as
$(\mathcal{M},d_{\textrm{GHP}})$
as
![]() $n\to \infty$
. The limit
$n\to \infty$
. The limit
![]() $\mathscr{M}$
is an
$\mathscr{M}$
is an
![]() $\mathbb{R}$
-tree that, remarkably, differs from the well-studied CRT [Reference Gall12].
$\mathbb{R}$
-tree that, remarkably, differs from the well-studied CRT [Reference Gall12].
1.2 Noise sensitivity and stability
Noise sensitivity of Boolean functions captures whether resampling only a small,
![]() $\varepsilon$
-fraction, of the input bits of a function leads to an almost independent output. Since its introduction in ref. [Reference Benjamini, Kalai and Schramm7], this concept has found various applications in theoretical computer science [Reference Mossel, O’Donnell and Oleszkiewicz21] and probability theory [Reference Garban and Steif13]. Lubetzky and Steif [Reference Lubetzky and Steif19] initiated the study of the noise sensitivity of critical random graphs. Denote by
$\varepsilon$
-fraction, of the input bits of a function leads to an almost independent output. Since its introduction in ref. [Reference Benjamini, Kalai and Schramm7], this concept has found various applications in theoretical computer science [Reference Mossel, O’Donnell and Oleszkiewicz21] and probability theory [Reference Garban and Steif13]. Lubetzky and Steif [Reference Lubetzky and Steif19] initiated the study of the noise sensitivity of critical random graphs. Denote by
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
the graph that is obtained by independently resampling each edge according to its original
$\mathbb{G}^\varepsilon _{n,\lambda }$
the graph that is obtained by independently resampling each edge according to its original
![]() $ \mathrm{Ber}(p(n,\lambda ))$
distribution with probability
$ \mathrm{Ber}(p(n,\lambda ))$
distribution with probability
![]() $\varepsilon$
. They proved that the property that the graph contains a cycle of length in
$\varepsilon$
. They proved that the property that the graph contains a cycle of length in
![]() $(an^{1/3},bn^{1/3})$
is noise sensitive provided that
$(an^{1/3},bn^{1/3})$
is noise sensitive provided that
![]() $\varepsilon \gg n^{-1/3}$
. Heuristically, a threshold of
$\varepsilon \gg n^{-1/3}$
. Heuristically, a threshold of
![]() $n^{-1/3}$
for noise sensitivity of such ‘global’ graph properties seems plausible. Indeed, if
$n^{-1/3}$
for noise sensitivity of such ‘global’ graph properties seems plausible. Indeed, if
![]() $\varepsilon \gg n^{-1/3}$
, then the edges that are not resampled, and appear in the graph both before and after the noise operation, form a subcritical random graph in which the property in question is degenerate.
$\varepsilon \gg n^{-1/3}$
, then the edges that are not resampled, and appear in the graph both before and after the noise operation, form a subcritical random graph in which the property in question is degenerate.
Roberts and Şengül [Reference Roberts and Şengül23] established the noise sensitivity of properties related to the size of the largest component of
![]() $\mathbb{G}_{n,\lambda }$
, under the stronger assumption that
$\mathbb{G}_{n,\lambda }$
, under the stronger assumption that
![]() $\varepsilon \gg n^{-1/6}$
. Afterwards, the above heuristic was made rigour in ref. [Reference Lubetzky and Peled18] by Lubetzky and the second author, establishing that if
$\varepsilon \gg n^{-1/6}$
. Afterwards, the above heuristic was made rigour in ref. [Reference Lubetzky and Peled18] by Lubetzky and the second author, establishing that if
![]() $\varepsilon \gg n^{-1/3}$
both (i) the rescaled sizes and (ii) the rescaled measured metric spaces, obtained from the components of
$\varepsilon \gg n^{-1/3}$
both (i) the rescaled sizes and (ii) the rescaled measured metric spaces, obtained from the components of
![]() $\mathbb{G}_{n,\lambda }$
and
$\mathbb{G}_{n,\lambda }$
and
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
, are asymptotically independent (where the entire sensitivity regime was completed in ref. [Reference Frilet11]). On the other hand, if
$\mathbb{G}^\varepsilon _{n,\lambda }$
, are asymptotically independent (where the entire sensitivity regime was completed in ref. [Reference Frilet11]). On the other hand, if
![]() $\varepsilon \ll n^{-1/3}$
the effect of the noise was shown to be negligible. Rossignol identified non-trivial correlations when
$\varepsilon \ll n^{-1/3}$
the effect of the noise was shown to be negligible. Rossignol identified non-trivial correlations when
![]() $\varepsilon =tn^{-1/3}$
[Reference Rossignol24].
$\varepsilon =tn^{-1/3}$
[Reference Rossignol24].
In the same manner, the measured metric space
![]() $M_n\in \mathcal{M}$
is obtained from
$M_n\in \mathcal{M}$
is obtained from
![]() ${\mathbb{M}}_n$
, let
${\mathbb{M}}_n$
, let
![]() $M_n^\varepsilon \in \mathcal{M}$
denote the measured metric space obtained from
$M_n^\varepsilon \in \mathcal{M}$
denote the measured metric space obtained from
![]() ${\mathbb{M}}_n^\varepsilon$
by rescaling the graph distances by
${\mathbb{M}}_n^\varepsilon$
by rescaling the graph distances by
![]() $n^{-1/3}$
and assigning a uniform measure on the vertices. Our main theorem establishes a noise threshold of
$n^{-1/3}$
and assigning a uniform measure on the vertices. Our main theorem establishes a noise threshold of
![]() $n^{-1/3}$
for any sequence of functions that depend on the scaled measured metric space. This threshold coincides with the noise threshold for critical random graphs and, accordingly, with the width of the critical window in the Erdős-Rényi phase transition.
$n^{-1/3}$
for any sequence of functions that depend on the scaled measured metric space. This threshold coincides with the noise threshold for critical random graphs and, accordingly, with the width of the critical window in the Erdős-Rényi phase transition.
Theorem 1.1.
Let
![]() $\varepsilon =\varepsilon _n\gt 0$
. Then, as
$\varepsilon =\varepsilon _n\gt 0$
. Then, as
![]() $n\to \infty$
,
$n\to \infty$
,
-
1. If
 $\varepsilon ^{3}n\to \infty$
then the pair
$\varepsilon ^{3}n\to \infty$
then the pair
 $\left (M_n,M_{n}^{\varepsilon }\right )$
converges in distribution to a pair of independent copies of
$\left (M_n,M_{n}^{\varepsilon }\right )$
converges in distribution to a pair of independent copies of
 $\mathscr{M}$
in
$\mathscr{M}$
in
 $(\mathcal{M},d_{\textrm{GHP}})$
.
$(\mathcal{M},d_{\textrm{GHP}})$
. -
2. If
 $\varepsilon ^{3}n\to 0$
then
$\varepsilon ^{3}n\to 0$
then
 $ d_{\textrm{GHP}}(M_{n},M_{n}^{\varepsilon })\overset{p}{\to }0$
.
$ d_{\textrm{GHP}}(M_{n},M_{n}^{\varepsilon })\overset{p}{\to }0$
.
For any sequence
![]() $f_n({\mathbb{M}}_n)\;:\!=\;\textbf{1}_{M_n\in S}$
of Boolean functions, where
$f_n({\mathbb{M}}_n)\;:\!=\;\textbf{1}_{M_n\in S}$
of Boolean functions, where
![]() $S$
is a continuity set of the limit space
$S$
is a continuity set of the limit space
![]() $\mathscr{M}$
, our theorem implies
$\mathscr{M}$
, our theorem implies
![]() $\varepsilon$
-noise sensitivity if
$\varepsilon$
-noise sensitivity if
![]() $\varepsilon \gg n^{-1/3}$
in Part (1), and
$\varepsilon \gg n^{-1/3}$
in Part (1), and
![]() $\varepsilon$
-noise stability if
$\varepsilon$
-noise stability if
![]() $\varepsilon \ll n^{-1/3}$
in Part (2). For concrete examples, indicator functions of properties such as ‘the diameter of the tree is at most
$\varepsilon \ll n^{-1/3}$
in Part (2). For concrete examples, indicator functions of properties such as ‘the diameter of the tree is at most
![]() $b\cdot n^{1/3}$
’, or ‘the average distance between a pair of vertices is greater than
$b\cdot n^{1/3}$
’, or ‘the average distance between a pair of vertices is greater than
![]() $a\cdot n^{1/3}$
’ naturally arise. However, we leave the verification that these examples indeed correspond to continuity sets of
$a\cdot n^{1/3}$
’ naturally arise. However, we leave the verification that these examples indeed correspond to continuity sets of
![]() $\mathscr{M}$
for future work (see Section 5), noting that it appears to follow from the recent explicit construction of
$\mathscr{M}$
for future work (see Section 5), noting that it appears to follow from the recent explicit construction of
![]() $\mathscr{M}$
as the Brownian parabolic tree [Reference Broutin and Marckert9].
$\mathscr{M}$
as the Brownian parabolic tree [Reference Broutin and Marckert9].
1.3 The random minimum spanning forest
Following [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4], our approach for Theorem 1.1 starts by investigating the effect of the noise operator on the metric structure of
![]() ${\mathbb{M}}_{n,\lambda }$
. The forest
${\mathbb{M}}_{n,\lambda }$
. The forest
![]() ${\mathbb{M}}^\varepsilon _{n,\lambda }$
denotes the MSF of the graph
${\mathbb{M}}^\varepsilon _{n,\lambda }$
denotes the MSF of the graph
![]() $\mathbb{G}^\varepsilon _{n,\lambda } \;:\!=\; \{e\in K_n\,:\,w_e^{\varepsilon }\le p(n,\lambda )\}$
endowed with weights from
$\mathbb{G}^\varepsilon _{n,\lambda } \;:\!=\; \{e\in K_n\,:\,w_e^{\varepsilon }\le p(n,\lambda )\}$
endowed with weights from
![]() $W_n^\varepsilon .$
$W_n^\varepsilon .$
For an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
and an integer
$G$
and an integer
![]() $j\ge 1$
, let
$j\ge 1$
, let
![]() ${\mathcal{S}}_j(G)$
be obtained from the
${\mathcal{S}}_j(G)$
be obtained from the
![]() $j$
-th largest connected component of
$j$
-th largest connected component of
![]() $G$
by rescaling the graph distances by
$G$
by rescaling the graph distances by
![]() $n^{-1/3}$
and assigning each vertex a measure of
$n^{-1/3}$
and assigning each vertex a measure of
![]() $n^{-2/3}.$
We denote by
$n^{-2/3}.$
We denote by
![]() ${\mathcal{S}}(G)$
the sequence
${\mathcal{S}}(G)$
the sequence
![]() ${\mathcal{S}}(G)=({\mathcal{S}}_j(G))_{j\ge 1}$
of elements in
${\mathcal{S}}(G)=({\mathcal{S}}_j(G))_{j\ge 1}$
of elements in
![]() $\mathcal{M}$
. We consider the two sequences of scaled measured metric spaces, given by
$\mathcal{M}$
. We consider the two sequences of scaled measured metric spaces, given by
![]() $M_{n,\lambda }\;:\!=\;{\mathcal{S}}({\mathbb{M}}_{n,\lambda })$
and
$M_{n,\lambda }\;:\!=\;{\mathcal{S}}({\mathbb{M}}_{n,\lambda })$
and
![]() $M_{n,\lambda }^\varepsilon \;:\!=\;{\mathcal{S}}({\mathbb{M}}^\varepsilon _{n,\lambda })$
. For every two sequences
$M_{n,\lambda }^\varepsilon \;:\!=\;{\mathcal{S}}({\mathbb{M}}^\varepsilon _{n,\lambda })$
. For every two sequences
![]() $S,S'$
of elements in
$S,S'$
of elements in
![]() $\mathcal{M}$
, let
$\mathcal{M}$
, let
![]() $d_{\textrm{GHP}}^4(S,S') = (\sum _j d_{\textrm{GHP}}(S_j,S_j')^4)^{\frac 14}$
and set
$d_{\textrm{GHP}}^4(S,S') = (\sum _j d_{\textrm{GHP}}(S_j,S_j')^4)^{\frac 14}$
and set
![]() $\mathbb{L}_4=\{ S\in \mathcal{M}^{\mathbb N}: \sum _j d_{\textrm{GHP}}(S_j,\textsf{Z})^4\lt \infty \}$
where
$\mathbb{L}_4=\{ S\in \mathcal{M}^{\mathbb N}: \sum _j d_{\textrm{GHP}}(S_j,\textsf{Z})^4\lt \infty \}$
where
![]() $\textsf{Z}$
is the zero metric space.
$\textsf{Z}$
is the zero metric space.
It is shown in ref. [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4] that there exists a sequence
![]() $\mathscr{M}_{\lambda }\;:\!=\;(\mathscr{M}_{\lambda,j})_{j\ge 1}$
of random compact measured metric spaces such that
$\mathscr{M}_{\lambda }\;:\!=\;(\mathscr{M}_{\lambda,j})_{j\ge 1}$
of random compact measured metric spaces such that
![]() $M_{n,\lambda } \to \mathscr{M}_{\lambda }$
as
$M_{n,\lambda } \to \mathscr{M}_{\lambda }$
as
![]() $n\to \infty$
in distribution in
$n\to \infty$
in distribution in
![]() $(\mathbb{L}_4,d_{\textrm{GHP}}^4).$
The connection between
$(\mathbb{L}_4,d_{\textrm{GHP}}^4).$
The connection between
![]() ${\mathbb{M}}_n$
and
${\mathbb{M}}_n$
and
![]() ${\mathbb{M}}_{n,\lambda }$
from [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4, Theorem 1.2] that was mentioned above can be now stated precisely. That is, if we let
${\mathbb{M}}_{n,\lambda }$
from [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4, Theorem 1.2] that was mentioned above can be now stated precisely. That is, if we let
![]() $\;\;\;\hat{\!\!\!\mathscr{M}}_{\lambda,1}$
be obtained from
$\;\;\;\hat{\!\!\!\mathscr{M}}_{\lambda,1}$
be obtained from
![]() $\mathscr{M}_{\lambda,1}$
by renormalizing its measure to a probability measure, then
$\mathscr{M}_{\lambda,1}$
by renormalizing its measure to a probability measure, then
![]() $\;\;\;\hat{\!\!\!\mathscr{M}}_{\lambda,1}\xrightarrow{\,\mathrm{d}\,} \mathscr{M}$
in
$\;\;\;\hat{\!\!\!\mathscr{M}}_{\lambda,1}\xrightarrow{\,\mathrm{d}\,} \mathscr{M}$
in
![]() $d_{\textrm{GHP}}$
as
$d_{\textrm{GHP}}$
as
![]() $\lambda \to \infty$
. Hence, Theorem 1.1 is derived from the following theorem.
$\lambda \to \infty$
. Hence, Theorem 1.1 is derived from the following theorem.
Theorem 1.2.
Let
![]() $\lambda \in{\mathbb{R}}$
and
$\lambda \in{\mathbb{R}}$
and
![]() $\varepsilon =\varepsilon _n\gt 0$
.
$\varepsilon =\varepsilon _n\gt 0$
.
-
1. If
 $\varepsilon ^{3}n\to \infty$
as
$\varepsilon ^{3}n\to \infty$
as
 $n\to \infty$
, then the pair
$n\to \infty$
, then the pair
 $\left (M_{n,\lambda },M_{n,\lambda }^\varepsilon \right )$
converges in distribution to a pair of independent copies of
$\left (M_{n,\lambda },M_{n,\lambda }^\varepsilon \right )$
converges in distribution to a pair of independent copies of
 $\mathscr{M}_{\lambda }$
in
$\mathscr{M}_{\lambda }$
in
 $(\mathbb{L}_4,d_{\textrm{GHP}}^4)$
.
$(\mathbb{L}_4,d_{\textrm{GHP}}^4)$
. -
2. If
 $\varepsilon ^{3}n\to 0$
as
$\varepsilon ^{3}n\to 0$
as
 $n\to \infty$
, then
$n\to \infty$
, then
 $d_{\textrm{GHP}}^4(M_{n,\lambda },M_{n,\lambda }^{\varepsilon })\overset{p}{\to }0.$
$d_{\textrm{GHP}}^4(M_{n,\lambda },M_{n,\lambda }^{\varepsilon })\overset{p}{\to }0.$
The noise sensitivity of critical random graphs from [Reference Lubetzky and Peled18] and [Reference Frilet11] establishes that if
![]() $\varepsilon ^{3}n\to \infty$
then the scaled measure metric spaces of the components of
$\varepsilon ^{3}n\to \infty$
then the scaled measure metric spaces of the components of
![]() $\mathbb{G}_{n,\lambda }$
and
$\mathbb{G}_{n,\lambda }$
and
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
are asymptotically independent. This fact seemingly excludes any non-negligible correlation between the scaled measure metric spaces of
$\mathbb{G}^\varepsilon _{n,\lambda }$
are asymptotically independent. This fact seemingly excludes any non-negligible correlation between the scaled measure metric spaces of
![]() ${\mathbb{M}}_{n,\lambda }$
and
${\mathbb{M}}_{n,\lambda }$
and
![]() ${\mathbb{M}}^\varepsilon _{n,\lambda }$
, which are obtained from
${\mathbb{M}}^\varepsilon _{n,\lambda }$
, which are obtained from
![]() $\mathbb{G}_{n,\lambda }$
and
$\mathbb{G}_{n,\lambda }$
and
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
respectively by the cycle-breaking algorithm. However, the existence of ‘bad’ edges that participate in cycles in both graphs, and with the same (not resampled) weight, may correlate the two runs of the cycle-breaking algorithm. We analyse the joint cycle-breaking algorithm and prove that if
$\mathbb{G}^\varepsilon _{n,\lambda }$
respectively by the cycle-breaking algorithm. However, the existence of ‘bad’ edges that participate in cycles in both graphs, and with the same (not resampled) weight, may correlate the two runs of the cycle-breaking algorithm. We analyse the joint cycle-breaking algorithm and prove that if
![]() $\varepsilon ^{3}n\to \infty$
then, with high probability, the number of such ‘bad’ edges is too small to generate a non-negligible correlation. For the stability part, we show that if
$\varepsilon ^{3}n\to \infty$
then, with high probability, the number of such ‘bad’ edges is too small to generate a non-negligible correlation. For the stability part, we show that if
![]() $\varepsilon ^{3}n\to 0$
then, typically, the two runs of the cycle-breaking algorithm are identical.
$\varepsilon ^{3}n\to 0$
then, typically, the two runs of the cycle-breaking algorithm are identical.
The remainder of the paper is organized as follows. Section 2 contains some preliminaries and additional background material needed for the proof of the main results. In Section 3, we prove both parts of Theorem 1.2, and in Section 4, we complete the proof of Theorem 1.1. We conclude with some open problems in Section 5.
2. Preliminaries
2.1 Notations
For clarity, we briefly recall the notations that were interspersed within the introduction and present some additional concepts needed in the proofs. Let
![]() $n$
be an integer and
$n$
be an integer and
![]() $K_n$
the complete
$K_n$
the complete
![]() $n$
-vertex graph. The edges of
$n$
-vertex graph. The edges of
![]() $K_n$
are assigned independent and
$K_n$
are assigned independent and
![]() $\mathrm{U}[0,1]$
-distributed weights
$\mathrm{U}[0,1]$
-distributed weights
![]() $W_n\;:\!=\;(w_e)_{e\in K_n}$
. Given a noise parameter
$W_n\;:\!=\;(w_e)_{e\in K_n}$
. Given a noise parameter
![]() $\varepsilon =\varepsilon _n$
, we define the weights
$\varepsilon =\varepsilon _n$
, we define the weights
![]() $W_n^\varepsilon \;:\!=\;(w^{\varepsilon }_e)_{e\in K_n}$
by
$W_n^\varepsilon \;:\!=\;(w^{\varepsilon }_e)_{e\in K_n}$
by
 \begin{equation*} w^\varepsilon _e \;:\!=\; \begin {cases} w_e & b_e = 0 \\ w'_e & b_e =1 \\ \end {cases}, \end{equation*}
\begin{equation*} w^\varepsilon _e \;:\!=\; \begin {cases} w_e & b_e = 0 \\ w'_e & b_e =1 \\ \end {cases}, \end{equation*}
where
![]() $b_e$
is an independent
$b_e$
is an independent
![]() $\mathrm{Ber}(\varepsilon )$
random variable and
$\mathrm{Ber}(\varepsilon )$
random variable and
![]() $w'_e$
is an independent
$w'_e$
is an independent
![]() $\mathrm{U}[0,1]$
-distributed weight. In words, we independently, with probability
$\mathrm{U}[0,1]$
-distributed weight. In words, we independently, with probability
![]() $\varepsilon$
, resample the weight of each edge.
$\varepsilon$
, resample the weight of each edge.
All the random graphs we study are measurable with respect to
![]() $W_n,W_n^\varepsilon$
. Namely,
$W_n,W_n^\varepsilon$
. Namely,
![]() ${\mathbb{M}}_n,{\mathbb{M}}_n^\varepsilon$
are the minimum spanning trees (MST) of
${\mathbb{M}}_n,{\mathbb{M}}_n^\varepsilon$
are the minimum spanning trees (MST) of
![]() $K_n$
under the weights
$K_n$
under the weights
![]() $W_n,W_n^\varepsilon$
respectively. In addition, we always refer to
$W_n,W_n^\varepsilon$
respectively. In addition, we always refer to
![]() $p$
as
$p$
as
![]() $p\;:\!=\;p(n,\lambda )=1/n+\lambda/n^{4/3}$
, where
$p\;:\!=\;p(n,\lambda )=1/n+\lambda/n^{4/3}$
, where
![]() $\lambda \in{\mathbb{R}}$
, and denote the random graphs
$\lambda \in{\mathbb{R}}$
, and denote the random graphs
Note that as random (unweighted) graphs,
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
is obtained from
$\mathbb{G}^\varepsilon _{n,\lambda }$
is obtained from
![]() $\mathbb{G}_{n,\lambda }$
by applying the standard
$\mathbb{G}_{n,\lambda }$
by applying the standard
![]() $\varepsilon$
-noise operator that independently, with probability
$\varepsilon$
-noise operator that independently, with probability
![]() $\varepsilon$
, resamples each edge. We denote the intersection of these two graphs by
$\varepsilon$
, resamples each edge. We denote the intersection of these two graphs by
![]() $\mathbb{I}\;:\!=\;\mathbb{G}_{n,\lambda }\cap \mathbb{G}^\varepsilon _{n,\lambda }$
, and its subgraph
$\mathbb{I}\;:\!=\;\mathbb{G}_{n,\lambda }\cap \mathbb{G}^\varepsilon _{n,\lambda }$
, and its subgraph
consisting of the edges that appear in
![]() $\mathbb{G}_{n,\lambda }$
and whose weight was not resampled – and thus also appear in
$\mathbb{G}_{n,\lambda }$
and whose weight was not resampled – and thus also appear in
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
. We denote by
$\mathbb{G}^\varepsilon _{n,\lambda }$
. We denote by
![]() ${\mathbb{M}}_{n,\lambda }$
(resp.
${\mathbb{M}}_{n,\lambda }$
(resp.
![]() ${\mathbb{M}}^\varepsilon _{n,\lambda }$
) the minimum spanning forest (MSF) of
${\mathbb{M}}^\varepsilon _{n,\lambda }$
) the minimum spanning forest (MSF) of
![]() $\mathbb{G}_{n,\lambda }$
(resp.
$\mathbb{G}_{n,\lambda }$
(resp.
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
) when endowed with edge weights from
$\mathbb{G}^\varepsilon _{n,\lambda }$
) when endowed with edge weights from
![]() $W_n$
(resp.
$W_n$
(resp.
![]() $W_n^\varepsilon$
).
$W_n^\varepsilon$
).
To some of the random graphs above, we associate a scaled measured metric space in
![]() $\mathcal{M}$
. Recall that
$\mathcal{M}$
. Recall that
![]() ${\mathcal{S}}(G)$
is a sequence of elements in
${\mathcal{S}}(G)$
is a sequence of elements in
![]() $\mathcal{M}$
that is obtained from an
$\mathcal{M}$
that is obtained from an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
by ordering its components in decreasing size, rescaling the graph distances by
$G$
by ordering its components in decreasing size, rescaling the graph distances by
![]() $n^{-1/3}$
and assigning each vertex a measure of
$n^{-1/3}$
and assigning each vertex a measure of
![]() $n^{-2/3}.$
We denote
$n^{-2/3}.$
We denote
![]() $M_{n,\lambda }={\mathcal{S}}({\mathbb{M}}_{n,\lambda }),\,M_{n,\lambda }^\varepsilon ={\mathcal{S}}({\mathbb{M}}^\varepsilon _{n,\lambda }),\, G_{n,\lambda }={\mathcal{S}}(\mathbb{G}_{n,\lambda })$
and
$M_{n,\lambda }={\mathcal{S}}({\mathbb{M}}_{n,\lambda }),\,M_{n,\lambda }^\varepsilon ={\mathcal{S}}({\mathbb{M}}^\varepsilon _{n,\lambda }),\, G_{n,\lambda }={\mathcal{S}}(\mathbb{G}_{n,\lambda })$
and
![]() $G_{n,\lambda }^\varepsilon ={\mathcal{S}}(\mathbb{G}^\varepsilon _{n,\lambda }).$
We sometime refer to specific elements in these sequences, e.g.,
$G_{n,\lambda }^\varepsilon ={\mathcal{S}}(\mathbb{G}^\varepsilon _{n,\lambda }).$
We sometime refer to specific elements in these sequences, e.g.,
![]() $M_{n,\lambda,j}$
denotes the measured metric space obtained from the
$M_{n,\lambda,j}$
denotes the measured metric space obtained from the
![]() $j$
-th largest component
$j$
-th largest component
![]() $C_j(\mathbb{G}_{n,\lambda })$
of the graph
$C_j(\mathbb{G}_{n,\lambda })$
of the graph
![]() $\mathbb{G}_{n,\lambda }$
. In addition, given a connected graph
$\mathbb{G}_{n,\lambda }$
. In addition, given a connected graph
![]() $G$
, let
$G$
, let
![]() $\hat{{\mathcal{S}}}(G)$
be obtained from
$\hat{{\mathcal{S}}}(G)$
be obtained from
![]() $G$
by rescaling the graph distance by
$G$
by rescaling the graph distance by
![]() $n^{-1/3}$
and assigning a uniform probability measure on its vertices. We view
$n^{-1/3}$
and assigning a uniform probability measure on its vertices. We view
![]() $M_n = \hat{{\mathcal{S}}}({\mathbb{M}}_n)$
,
$M_n = \hat{{\mathcal{S}}}({\mathbb{M}}_n)$
,
![]() $M_n^\varepsilon = \hat{{\mathcal{S}}}({\mathbb{M}}_n^\varepsilon )$
as elements of
$M_n^\varepsilon = \hat{{\mathcal{S}}}({\mathbb{M}}_n^\varepsilon )$
as elements of
![]() $\mathcal{M}$
.
$\mathcal{M}$
.
2.2 The joint cycle-breaking algorithm
An alternative approach to the well-known Kruskal’s algorithm for finding the MSF of a weighted graph is the cycle-breaking algorithm, aka the reverse-delete algorithm, which was also introduced by Kruskal in ref. [Reference Kruskal17]. Consider
![]() $\mathrm{conn}(G)$
, the set of edges of
$\mathrm{conn}(G)$
, the set of edges of
![]() $G$
that participate in a cycle. In other words,
$G$
that participate in a cycle. In other words,
![]() $e\in \mathrm{conn}(G)$
if removing it does not increase the number of connected components. The algorithm finds the MSF of a given weighted graph
$e\in \mathrm{conn}(G)$
if removing it does not increase the number of connected components. The algorithm finds the MSF of a given weighted graph
![]() $G$
by sequentially removing the edge with the largest weight from
$G$
by sequentially removing the edge with the largest weight from
![]() $\mathrm{conn}(G)$
. Once the remaining graph is acyclic, its edges form the MSF of
$\mathrm{conn}(G)$
. Once the remaining graph is acyclic, its edges form the MSF of
![]() $G$
.
$G$
.
For a graph
![]() $G$
, let
$G$
, let
![]() $\mathcal{K}^{\infty }(G)$
denote the random MSF of
$\mathcal{K}^{\infty }(G)$
denote the random MSF of
![]() $G$
if the edges are given exchangeable, distinct random weights. In such a case,
$G$
if the edges are given exchangeable, distinct random weights. In such a case,
![]() $\mathcal{K}^{\infty }(G)$
can be sampled by running a cycle-breaking algorithm on
$\mathcal{K}^{\infty }(G)$
can be sampled by running a cycle-breaking algorithm on
![]() $G$
that removes a uniformly random edge from
$G$
that removes a uniformly random edge from
![]() $\mathrm{conn}(G)$
in each step. Indeed, the heaviest edge in
$\mathrm{conn}(G)$
in each step. Indeed, the heaviest edge in
![]() $\mathrm{conn}(G)$
is uniformly distributed, regardless of which edges were exposed as the heaviest in the previous steps of the algorithm. For example, conditioned on (the edge set of)
$\mathrm{conn}(G)$
is uniformly distributed, regardless of which edges were exposed as the heaviest in the previous steps of the algorithm. For example, conditioned on (the edge set of)
![]() $\mathbb{G}_{n,\lambda }$
, the forest
$\mathbb{G}_{n,\lambda }$
, the forest
![]() ${\mathbb{M}}_{n,\lambda }$
is
${\mathbb{M}}_{n,\lambda }$
is
![]() $\mathcal{K}^{\infty }(\mathbb{G}_{n,\lambda })$
-distributed.
$\mathcal{K}^{\infty }(\mathbb{G}_{n,\lambda })$
-distributed.
Given two finite graphs
![]() $G_1,G_2$
and a common subgraph
$G_1,G_2$
and a common subgraph
![]() $H\subset G_1\cap G_2$
, let
$H\subset G_1\cap G_2$
, let
![]() $W^i\;:\!=\;(w^i_e)_{e\in G_i},\,i=1,2,$
be two exchangeable random weights given to the edges of
$W^i\;:\!=\;(w^i_e)_{e\in G_i},\,i=1,2,$
be two exchangeable random weights given to the edges of
![]() $G_1$
and
$G_1$
and
![]() $G_2$
that are distinct except that
$G_2$
that are distinct except that
![]() $ w^1_e=w^2_e \iff e\in H.$
We denote by
$ w^1_e=w^2_e \iff e\in H.$
We denote by
![]() $\mathcal{K}^{\infty }_{\mathrm{joint}}(G_1,G_2,H)$
the joint distribution of the pair of minimum spanning forests of
$\mathcal{K}^{\infty }_{\mathrm{joint}}(G_1,G_2,H)$
the joint distribution of the pair of minimum spanning forests of
![]() $G_1,G_2$
under the above random edge weights
$G_1,G_2$
under the above random edge weights
![]() $W^1,W^2$
.
$W^1,W^2$
.
Clearly, the marginal distributions of
![]() $\mathcal{K}^{\infty }_{\mathrm{joint}}(G_1,G_2,H)$
are
$\mathcal{K}^{\infty }_{\mathrm{joint}}(G_1,G_2,H)$
are
![]() $\mathcal{K}^{\infty }(G_1)$
and
$\mathcal{K}^{\infty }(G_1)$
and
![]() $\mathcal{K}^{\infty }(G_2)$
. In addition, if
$\mathcal{K}^{\infty }(G_2)$
. In addition, if
![]() $H\cap \mathrm{conn}(G_1)\cap \mathrm{conn}(G_2)=\emptyset$
then
$H\cap \mathrm{conn}(G_1)\cap \mathrm{conn}(G_2)=\emptyset$
then
![]() $\mathcal{K}^{\infty }_{\mathrm{joint}}(G_1,G_2,H)=\mathcal{K}^{\infty }(G_1)\times \mathcal{K}^{\infty }(G_2)$
, i.e., the joint cycle-breaking algorithm can be carried out by two independent cycle-breaking algorithms on
$\mathcal{K}^{\infty }_{\mathrm{joint}}(G_1,G_2,H)=\mathcal{K}^{\infty }(G_1)\times \mathcal{K}^{\infty }(G_2)$
, i.e., the joint cycle-breaking algorithm can be carried out by two independent cycle-breaking algorithms on
![]() $G_1$
and
$G_1$
and
![]() $G_2$
. On the other extreme, if
$G_2$
. On the other extreme, if
![]() $\mathrm{conn}(G_1)=\mathrm{conn}(G_2)$
and
$\mathrm{conn}(G_1)=\mathrm{conn}(G_2)$
and
![]() $\mathrm{conn}(G_1)\subseteq H$
, then the exact same set of edges is removed in both graphs during the run of the joint cycle-breaking algorithm. In such a case, if
$\mathrm{conn}(G_1)\subseteq H$
, then the exact same set of edges is removed in both graphs during the run of the joint cycle-breaking algorithm. In such a case, if
![]() $(M_1,M_2)\sim \mathcal{K}^{\infty }_{\mathrm{joint}}(G_1,G_2,H)$
then
$(M_1,M_2)\sim \mathcal{K}^{\infty }_{\mathrm{joint}}(G_1,G_2,H)$
then
![]() $M_1\sim \mathcal{K}^{\infty }(G_1)$
and
$M_1\sim \mathcal{K}^{\infty }(G_1)$
and
![]() $M_2$
is then deterministically defined by
$M_2$
is then deterministically defined by
![]() $M_2=G_2\setminus (G_1\setminus M_1)$
.
$M_2=G_2\setminus (G_1\setminus M_1)$
.
The example prompting this definition in our study is that, conditioned on (the edge sets of)
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}}$
defined in section 2.1, the distribution of the pair
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}}$
defined in section 2.1, the distribution of the pair
![]() $({\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda })$
is
$({\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda })$
is
![]() $\mathcal{K}^{\infty }_{\mathrm{joint}}(\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}})$
. Indeed, among the edges in
$\mathcal{K}^{\infty }_{\mathrm{joint}}(\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}})$
. Indeed, among the edges in
![]() $\mathbb{G}_{n,\lambda }\cup \mathbb{G}^\varepsilon _{n,\lambda }$
, only those in
$\mathbb{G}_{n,\lambda }\cup \mathbb{G}^\varepsilon _{n,\lambda }$
, only those in
![]() $\check{\mathbb{I}}$
have the same weight in
$\check{\mathbb{I}}$
have the same weight in
![]() $W_n$
and
$W_n$
and
![]() $W_n^\varepsilon$
, and all the other weights are independent. Roughly speaking, the two extreme cases for
$W_n^\varepsilon$
, and all the other weights are independent. Roughly speaking, the two extreme cases for
![]() $H$
mentioned above describe what typically occurs in the noise sensitivity and stability regimes.
$H$
mentioned above describe what typically occurs in the noise sensitivity and stability regimes.
2.3 Scaling limits
We conclude this section by briefly reviewing previous works regarding the scaling limits of the measured metric spaces obtained from the random graphs that appear in our work. In ref. [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4] (building on results from [Reference Addario-Berry, Broutin and Goldschmidt2]), it is proved that there exists a sequence
![]() $\mathscr{G}_\lambda =(\mathscr{G}_{\lambda,j})_{j\ge 1}$
of random elements in
$\mathscr{G}_\lambda =(\mathscr{G}_{\lambda,j})_{j\ge 1}$
of random elements in
![]() $\mathcal{M}$
such that
$\mathcal{M}$
such that
![]() $G_{n,\lambda }\xrightarrow{\,\mathrm{d}\,} \mathscr{G}_\lambda$
in
$G_{n,\lambda }\xrightarrow{\,\mathrm{d}\,} \mathscr{G}_\lambda$
in
![]() $(\mathbb L_4,d_{\textrm{GHP}}^4)$
as
$(\mathbb L_4,d_{\textrm{GHP}}^4)$
as
![]() $n\to \infty$
. Furthermore, by defining a continuous version of the cycle-breaking algorithm (whose distribution is also denoted by
$n\to \infty$
. Furthermore, by defining a continuous version of the cycle-breaking algorithm (whose distribution is also denoted by
![]() $\mathcal{K}^{\infty }$
), they obtain a sequence
$\mathcal{K}^{\infty }$
), they obtain a sequence
![]() $\mathscr{M}_\lambda =(\mathscr{M}_{\lambda,j})_{j\ge 1}$
of random elements in
$\mathscr{M}_\lambda =(\mathscr{M}_{\lambda,j})_{j\ge 1}$
of random elements in
![]() $\mathcal{M}$
which is
$\mathcal{M}$
which is
![]() $\mathcal{K}^{\infty }(\mathscr{G}_\lambda )$
-distributed conditioned on
$\mathcal{K}^{\infty }(\mathscr{G}_\lambda )$
-distributed conditioned on
![]() $\mathscr{G}_\lambda$
. They prove that
$\mathscr{G}_\lambda$
. They prove that
![]() $M_{n,\lambda }\xrightarrow{\,\mathrm{d}\,} \mathscr{M}_\lambda$
in
$M_{n,\lambda }\xrightarrow{\,\mathrm{d}\,} \mathscr{M}_\lambda$
in
![]() $(\mathbb L_4,d_{\textrm{GHP}}^4)$
as
$(\mathbb L_4,d_{\textrm{GHP}}^4)$
as
![]() $n\to \infty$
by establishing the continuity of
$n\to \infty$
by establishing the continuity of
![]() $\mathcal{K}^{\infty }$
, and that the scaling limit
$\mathcal{K}^{\infty }$
, and that the scaling limit
![]() $\mathscr{M}$
of
$\mathscr{M}$
of
![]() $M_n$
is obtained by renormalizing the measure of
$M_n$
is obtained by renormalizing the measure of
![]() $\mathscr{M}_{\lambda,1}$
to a probability measure and taking
$\mathscr{M}_{\lambda,1}$
to a probability measure and taking
![]() $\lambda \to \infty$
(as mentioned in section 1).
$\lambda \to \infty$
(as mentioned in section 1).
3. Proof of Theorem 1.2
3.1 Noise sensitivity of the MSF
We saw that the pair
![]() $({\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda })$
is obtained by a joint cycle-breaking algorithm and that it is
$({\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda })$
is obtained by a joint cycle-breaking algorithm and that it is
![]() $\mathcal{K}^{\infty }_{\mathrm{joint}}(\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}})$
- distributed. Our first goal is to show that, if
$\mathcal{K}^{\infty }_{\mathrm{joint}}(\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}})$
- distributed. Our first goal is to show that, if
![]() $\varepsilon ^3n\to \infty$
, the joint cycle-breaking is close to two independent runs of the cycle-breaking algorithm. We start by bounding the number of edges that participate in a cycle in both graphs, and, as a result, can potentially correlate the two forests during the joint cycle-breaking.
$\varepsilon ^3n\to \infty$
, the joint cycle-breaking is close to two independent runs of the cycle-breaking algorithm. We start by bounding the number of edges that participate in a cycle in both graphs, and, as a result, can potentially correlate the two forests during the joint cycle-breaking.
Lemma 3.1.
Fix
![]() $\lambda \in{\mathbb{R}}$
and let
$\lambda \in{\mathbb{R}}$
and let
![]() $\varepsilon ^3 n\to \infty$
,
$\varepsilon ^3 n\to \infty$
,
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
as defined in §
2
, and
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
as defined in §
2
, and
![]() $\mathbb{J}= \mathrm{conn}(\mathbb{G}_{n,\lambda })\cap \mathrm{conn}(\mathbb{G}^\varepsilon _{n,\lambda }).$
Then,
$\mathbb{J}= \mathrm{conn}(\mathbb{G}_{n,\lambda })\cap \mathrm{conn}(\mathbb{G}^\varepsilon _{n,\lambda }).$
Then,
as
![]() $n\to \infty$
for every diverging sequence
$n\to \infty$
for every diverging sequence
![]() $\omega =\omega (n)\to \infty .$
$\omega =\omega (n)\to \infty .$
In the proof below, we denote by
![]() $G-e$
the subgraph of
$G-e$
the subgraph of
![]() $G$
on the same vertex set with the edge set
$G$
on the same vertex set with the edge set
![]() $E(G)\setminus \{e\}$
, and by
$E(G)\setminus \{e\}$
, and by
![]() $G\setminus A$
the subgraph of
$G\setminus A$
the subgraph of
![]() $G$
induced by the vertices that are not in the vertex subset
$G$
induced by the vertices that are not in the vertex subset
![]() $A$
.
$A$
.
Proof. Recall that
![]() $\mathbb{I}$
denotes the intersection
$\mathbb{I}$
denotes the intersection
![]() $\mathbb{G}_{n,\lambda } \cap \mathbb{G}^\varepsilon _{n,\lambda }$
. The graph
$\mathbb{G}_{n,\lambda } \cap \mathbb{G}^\varepsilon _{n,\lambda }$
. The graph
![]() $\mathbb{I}$
is a
$\mathbb{I}$
is a
![]() $\mathcal G(n,\theta )$
random graph, where
$\mathcal G(n,\theta )$
random graph, where
Fix some edge
![]() $e=\{u,v\}$
in
$e=\{u,v\}$
in
![]() $K_n$
. We consider two disjoint possibilities for the occurrence of the event
$K_n$
. We consider two disjoint possibilities for the occurrence of the event
![]() $e\in \mathbb{J}$
:
$e\in \mathbb{J}$
:
-
1. The event
 $A=A_e=\{e\in \mathrm{conn}(\mathbb{I})\}$
where
$A=A_e=\{e\in \mathrm{conn}(\mathbb{I})\}$
where
 $e$
belongs to a cycle that is contained in both graphs, or
$e$
belongs to a cycle that is contained in both graphs, or -
2. the event
 $B=B_e=\{e\in \mathbb{J}\setminus \mathrm{conn}(\mathbb{I})\}$
where there are two distinct cycles in
$B=B_e=\{e\in \mathbb{J}\setminus \mathrm{conn}(\mathbb{I})\}$
where there are two distinct cycles in
 $\mathbb{G}_{n,\lambda }$
and
$\mathbb{G}_{n,\lambda }$
and
 $\mathbb{G}^\varepsilon _{n,\lambda }$
both containing
$\mathbb{G}^\varepsilon _{n,\lambda }$
both containing
 $e$
, and there is no cycle in
$e$
, and there is no cycle in
 $\mathbb{I}$
containing
$\mathbb{I}$
containing
 $e.$
$e.$
We bound the probability of
![]() $A$
by observing it occurs if and only if
$A$
by observing it occurs if and only if
![]() $e\in \mathbb{I}$
and there is a path in the graph
$e\in \mathbb{I}$
and there is a path in the graph
![]() $\mathbb{I} - e$
from
$\mathbb{I} - e$
from
![]() $v$
to
$v$
to
![]() $u$
. By enumerating all the paths from
$u$
. By enumerating all the paths from
![]() $v$
to
$v$
to
![]() $u$
with
$u$
with
![]() $k\ge 1$
additional vertices we find that
$k\ge 1$
additional vertices we find that
 \begin{equation} \mathbb{P}(A) \le \theta \sum _{k\ge 1}n^k\theta ^{k+1} \le \frac{\theta ^3 n}{1-\theta n}= \frac{1+o(1)}{\varepsilon n^2}, \end{equation}
\begin{equation} \mathbb{P}(A) \le \theta \sum _{k\ge 1}n^k\theta ^{k+1} \le \frac{\theta ^3 n}{1-\theta n}= \frac{1+o(1)}{\varepsilon n^2}, \end{equation}
where the last inequality follows from the relations
![]() $\theta \le 1/n$
and
$\theta \le 1/n$
and
![]() $1-\theta n=\varepsilon (1+o(1))$
.
$1-\theta n=\varepsilon (1+o(1))$
.

Figure 1. The three combinations of internal and external paths between
![]() $u$
and
$u$
and
![]() $v$
that can cause the occurrence of
$v$
that can cause the occurrence of
![]() $B$
.
$B$
.
Next, we turn to bound the probability of
![]() $B$
. Let
$B$
. Let
![]() $C_x$
, for
$C_x$
, for
![]() $x\in \{u,v\}$
, denote the component of the vertex
$x\in \{u,v\}$
, denote the component of the vertex
![]() $x$
in the graph
$x$
in the graph
![]() $\mathbb{I}-e$
. We further denote
$\mathbb{I}-e$
. We further denote
![]() $\mathbb K_1\;:\!=\;\mathbb{G}_{n,\lambda }\setminus (C_u\cup C_v)$
and
$\mathbb K_1\;:\!=\;\mathbb{G}_{n,\lambda }\setminus (C_u\cup C_v)$
and
![]() $\mathbb K_2\;:\!=\;\mathbb{G}^\varepsilon _{n,\lambda }\setminus (C_u\cup C_v)$
.
$\mathbb K_2\;:\!=\;\mathbb{G}^\varepsilon _{n,\lambda }\setminus (C_u\cup C_v)$
.
Claim 3.2.
For every
![]() $C_u,C_v, \mathbb K_1,\mathbb K_2$
as above there holds
$C_u,C_v, \mathbb K_1,\mathbb K_2$
as above there holds
 \begin{equation*} \mathbb {P}(B\,|\,C_u,C_v,\mathbb K_1,\mathbb K_2) \le \textbf {1}_{C_u\ne C_v}\cdot \theta \cdot (|C_u||C_v|)^2\cdot \prod _{i=1}^{2}\left (\rho +\rho ^2\sum _{j\ge 1}|C_j(\mathbb K_i)|^2\right )\,, \end{equation*}
\begin{equation*} \mathbb {P}(B\,|\,C_u,C_v,\mathbb K_1,\mathbb K_2) \le \textbf {1}_{C_u\ne C_v}\cdot \theta \cdot (|C_u||C_v|)^2\cdot \prod _{i=1}^{2}\left (\rho +\rho ^2\sum _{j\ge 1}|C_j(\mathbb K_i)|^2\right )\,, \end{equation*}
where
![]() $ \rho \;:\!=\; p\varepsilon (1-p)/(1-\theta ).$
$ \rho \;:\!=\; p\varepsilon (1-p)/(1-\theta ).$
Proof. We first note that
![]() $C_u$
is either equal or disjoint to
$C_u$
is either equal or disjoint to
![]() $C_v$
, and that in the former case there exists a path from
$C_v$
, and that in the former case there exists a path from
![]() $v$
to
$v$
to
![]() $u$
in
$u$
in
![]() $\mathbb{I} - e$
. We observe that if
$\mathbb{I} - e$
. We observe that if
![]() $C_u=C_v$
then the event
$C_u=C_v$
then the event
![]() $B$
does not occur, hence both sides in the claimed inequality are equal to
$B$
does not occur, hence both sides in the claimed inequality are equal to
![]() $0$
. Indeed, this is derived directly by combining the facts
$0$
. Indeed, this is derived directly by combining the facts
![]() $B\subseteq \{e\in \mathbb{I}\}\cap A^c$
and
$B\subseteq \{e\in \mathbb{I}\}\cap A^c$
and
![]() $A=\{e\in \mathbb{I}\}\cap \{C_u=C_v\}.$
$A=\{e\in \mathbb{I}\}\cap \{C_u=C_v\}.$
Suppose that
![]() $C_u\cap C_v=\emptyset$
, and consider the edge sets
$C_u\cap C_v=\emptyset$
, and consider the edge sets
and
Note that for every
![]() $f\in F_0\cup F_1$
, the only information that is exposed by our conditioning is that
$f\in F_0\cup F_1$
, the only information that is exposed by our conditioning is that
![]() $f\notin \mathbb{I}$
. Therefore, for every two edge subsets
$f\notin \mathbb{I}$
. Therefore, for every two edge subsets
![]() $L_1,L_2\subset F_0\cup F_1$
there holds
$L_1,L_2\subset F_0\cup F_1$
there holds
Indeed, if
![]() $L_1\cap L_2\ne \emptyset$
then this conditional probability is
$L_1\cap L_2\ne \emptyset$
then this conditional probability is
![]() $0$
since no edge of
$0$
since no edge of
![]() $F_0\cup F_1$
is in
$F_0\cup F_1$
is in
![]() $\mathbb{I}$
. Otherwise, by the independence between the different edges, (3.2) follows from the fact that, for every edge
$\mathbb{I}$
. Otherwise, by the independence between the different edges, (3.2) follows from the fact that, for every edge
![]() $f$
,
$f$
,
![]() $ \mathbb{P}(f\in \mathbb{G}_{n,\lambda }\,|\,f\notin \mathbb{I})=\mathbb{P}(f\in \mathbb{G}^\varepsilon _{n,\lambda }\,|\,f\notin \mathbb{I})=\rho .$
$ \mathbb{P}(f\in \mathbb{G}_{n,\lambda }\,|\,f\notin \mathbb{I})=\mathbb{P}(f\in \mathbb{G}^\varepsilon _{n,\lambda }\,|\,f\notin \mathbb{I})=\rho .$
We consider two different partitions of
![]() $F_1$
given by
$F_1$
given by
where
![]() $F_{x,j,i}$
consists of all the edges between
$F_{x,j,i}$
consists of all the edges between
![]() $C_x$
and the
$C_x$
and the
![]() $j$
-th largest connected component
$j$
-th largest connected component
![]() $C_j(\mathbb{K}_i)$
of the graph
$C_j(\mathbb{K}_i)$
of the graph
![]() $\mathbb{K}_i$
. A path from
$\mathbb{K}_i$
. A path from
![]() $v$
to
$v$
to
![]() $u$
in
$u$
in
![]() $\mathbb{G}_{n,\lambda } - e$
can either be internal and involve an edge from
$\mathbb{G}_{n,\lambda } - e$
can either be internal and involve an edge from
![]() $F_0$
, or be external and involve one edge from
$F_0$
, or be external and involve one edge from
![]() $F_{v,j,1}$
and one from
$F_{v,j,1}$
and one from
![]() $F_{u,j,1}$
for some
$F_{u,j,1}$
for some
![]() $j\ge 1$
, using the edges from
$j\ge 1$
, using the edges from
![]() $C_j(\mathbb{K}_1)$
to complete the path. Clearly, a similar statement holds for
$C_j(\mathbb{K}_1)$
to complete the path. Clearly, a similar statement holds for
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
where
$\mathbb{G}^\varepsilon _{n,\lambda }$
where
![]() $F_{x,j,1}$
is replaced by
$F_{x,j,1}$
is replaced by
![]() $F_{x,j,2}$
for both
$F_{x,j,2}$
for both
![]() $x\in \{u,v\}$
(See Fig. 1). Therefore, we claim that
$x\in \{u,v\}$
(See Fig. 1). Therefore, we claim that
 \begin{align} \nonumber & \mathbb{P}(B\,|\,C_v,C_u,\mathbb{K}_1,\mathbb{K}_2) \le \\ \nonumber & \quad \le \, \textbf{1}_{C_u\ne C_v}\cdot \theta \cdot \left (\rho ^2|F_0|^2 +\rho ^3|F_0|\sum _{i=1}^{2}\sum _{j\ge 1}\ |F_{v,j,i}||F_{u,j,i}| +\rho ^4\prod _{i=1}^{2}\sum _{j\ge 1}\ |F_{u,j,i}||F_{v,j,i}|\right ) \\ & \quad= \textbf{1}_{C_u\ne C_v}\cdot \theta \cdot \prod _{i=1}^{2}\left (\rho |F_0|+\rho ^2\sum _{j\ge 1}\ |F_{u,j,i}||F_{v,j,i}|\right ). \end{align}
\begin{align} \nonumber & \mathbb{P}(B\,|\,C_v,C_u,\mathbb{K}_1,\mathbb{K}_2) \le \\ \nonumber & \quad \le \, \textbf{1}_{C_u\ne C_v}\cdot \theta \cdot \left (\rho ^2|F_0|^2 +\rho ^3|F_0|\sum _{i=1}^{2}\sum _{j\ge 1}\ |F_{v,j,i}||F_{u,j,i}| +\rho ^4\prod _{i=1}^{2}\sum _{j\ge 1}\ |F_{u,j,i}||F_{v,j,i}|\right ) \\ & \quad= \textbf{1}_{C_u\ne C_v}\cdot \theta \cdot \prod _{i=1}^{2}\left (\rho |F_0|+\rho ^2\sum _{j\ge 1}\ |F_{u,j,i}||F_{v,j,i}|\right ). \end{align}
Indeed, every term in the second line corresponds to a different combination of internal and external paths. The first term corresponds to having two internal paths so we have
![]() $|F_0|^2$
choices for having an edge from
$|F_0|^2$
choices for having an edge from
![]() $F_0$
in both graphs, and the probability that the two edges actually appear is at most
$F_0$
in both graphs, and the probability that the two edges actually appear is at most
![]() $\rho ^2$
by (3.2). Similarly, the second term accounts for having one internal and one external path, where for the external path, say in
$\rho ^2$
by (3.2). Similarly, the second term accounts for having one internal and one external path, where for the external path, say in
![]() $\mathbb{G}_{n,\lambda }$
, we need to choose the component
$\mathbb{G}_{n,\lambda }$
, we need to choose the component
![]() $C_j(\mathbb{K}_1)$
we use, as well as an edge from
$C_j(\mathbb{K}_1)$
we use, as well as an edge from
![]() $F_{u,j,1}$
and an edge from
$F_{u,j,1}$
and an edge from
![]() $F_{v,j,1}$
. We multiply by
$F_{v,j,1}$
. We multiply by
![]() $\rho ^3\cdot |F_0|$
, since in addition to having these two edges appear in
$\rho ^3\cdot |F_0|$
, since in addition to having these two edges appear in
![]() $\mathbb{G}_{n,\lambda }$
, we also choose an edge from
$\mathbb{G}_{n,\lambda }$
, we also choose an edge from
![]() $F_0$
to appear in
$F_0$
to appear in
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
. The last term is derived by considering the case of two external paths, as we need to choose, for both graphs
$\mathbb{G}^\varepsilon _{n,\lambda }$
. The last term is derived by considering the case of two external paths, as we need to choose, for both graphs
![]() $ \mathbb{K}_i$
, a component
$ \mathbb{K}_i$
, a component
![]() $C_j( \mathbb{K}_i)$
, and edges from
$C_j( \mathbb{K}_i)$
, and edges from
![]() $F_{v,j,i}$
and
$F_{v,j,i}$
and
![]() $F_{u,j,i}.$
To conclude, note the multiplicative term
$F_{u,j,i}.$
To conclude, note the multiplicative term
![]() $\theta$
accounting for the event
$\theta$
accounting for the event
![]() $e\in \mathbb{I}$
. Alternatively, (3.3) can be understood as letting each of the graphs
$e\in \mathbb{I}$
. Alternatively, (3.3) can be understood as letting each of the graphs
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
either choose an internal path with a cost of
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
either choose an internal path with a cost of
![]() $\rho$
or an external path with a cost of
$\rho$
or an external path with a cost of
![]() $\rho ^2$
. The product of these two terms appears due to the negative correlations from (3.2). The claim is derived from (3.3) by noting that
$\rho ^2$
. The product of these two terms appears due to the negative correlations from (3.2). The claim is derived from (3.3) by noting that
![]() $|F_0|\lt |C_u||C_v|$
,
$|F_0|\lt |C_u||C_v|$
,
![]() $|F_{x,j,i}|=|C_x||C_j(\mathbb{K}_i)|$
for every
$|F_{x,j,i}|=|C_x||C_j(\mathbb{K}_i)|$
for every
![]() $x,j$
and
$x,j$
and
![]() $i$
, and a straightforward manipulation.
$i$
, and a straightforward manipulation.
We proceed by observing that
since
![]() $\mathbb K_1,\mathbb K_2$
are subgraphs of
$\mathbb K_1,\mathbb K_2$
are subgraphs of
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
respectively.
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
respectively.
Next, for a positive
![]() $c\in{\mathbb{R}}$
, denote by
$c\in{\mathbb{R}}$
, denote by
![]() $E_c$
the event that
$E_c$
the event that
 \begin{equation*} \max \left \{\sum _{j\ge 1}|C_j(\mathbb {G}_{n,\lambda })|^2,\sum _{j\ge 1}|C_j(\mathbb {G}^\varepsilon _{n,\lambda })|^2\right \} \le cn^{4/3}, \end{equation*}
\begin{equation*} \max \left \{\sum _{j\ge 1}|C_j(\mathbb {G}_{n,\lambda })|^2,\sum _{j\ge 1}|C_j(\mathbb {G}^\varepsilon _{n,\lambda })|^2\right \} \le cn^{4/3}, \end{equation*}
and recall that [Reference Lubetzky and Peled18, Theorem 1], [Reference Frilet11] establish that if
![]() $\varepsilon ^3n\to \infty$
then the pair
$\varepsilon ^3n\to \infty$
then the pair
weakly converges in
![]() $\ell _2$
to a pair of independent copies of a random sequence whose law was identified by Aldous [Reference Aldous5]. Therefore,
$\ell _2$
to a pair of independent copies of a random sequence whose law was identified by Aldous [Reference Aldous5]. Therefore,
By combining (3.4) and Claim 3.2 we find that
Let
![]() $Y$
denote the size of the connected component of a fixed vertex in a
$Y$
denote the size of the connected component of a fixed vertex in a
![]() $\mathcal{G}(n,\theta )$
random graph. Note that for every choice of
$\mathcal{G}(n,\theta )$
random graph. Note that for every choice of
![]() $C_u$
, the random variable
$C_u$
, the random variable
![]() $\textbf{1}_{C_u\ne C_v}|C_v|^2$
is stochastically bounded from above by
$\textbf{1}_{C_u\ne C_v}|C_v|^2$
is stochastically bounded from above by
![]() $Y^2$
. Indeed, If
$Y^2$
. Indeed, If
![]() $v\in C_u$
then
$v\in C_u$
then
![]() $\textbf{1}_{C_u\ne C_v}=0$
. Otherwise,
$\textbf{1}_{C_u\ne C_v}=0$
. Otherwise,
![]() $C_v$
is the component of
$C_v$
is the component of
![]() $v$
in the
$v$
in the
![]() $\mathcal G(n-|C_u|,\theta )$
random graph
$\mathcal G(n-|C_u|,\theta )$
random graph
![]() $\mathbb{I}\setminus C_u$
. As a result,
$\mathbb{I}\setminus C_u$
. As a result,
![]() $|C_v|$
is indeed dominated by
$|C_v|$
is indeed dominated by
![]() $Y$
. Therefore,
$Y$
. Therefore,
 \begin{align} \nonumber \mathbb{E}[\textbf{1}_{C_u\ne C_v}(|C_u||C_v|)^2] =\, &\mathbb{E}\left [|C_u|^2\cdot \mathbb{E}\left [ \left . \textbf{1}_{C_u\ne C_v}|C_v|^2\,\right |\,C_u\right ]\right ]\\ \le \,& \mathbb{E}\left [|C_u|^2 \right ]\mathbb{E}[Y^2] \nonumber \\ \le \,& \mathbb{E}[Y^2]^2. \end{align}
\begin{align} \nonumber \mathbb{E}[\textbf{1}_{C_u\ne C_v}(|C_u||C_v|)^2] =\, &\mathbb{E}\left [|C_u|^2\cdot \mathbb{E}\left [ \left . \textbf{1}_{C_u\ne C_v}|C_v|^2\,\right |\,C_u\right ]\right ]\\ \le \,& \mathbb{E}\left [|C_u|^2 \right ]\mathbb{E}[Y^2] \nonumber \\ \le \,& \mathbb{E}[Y^2]^2. \end{align}
In addition,
 \begin{equation} \mathbb{E}[Y^2] = \frac 1n\mathbb{E}_{G\sim \mathcal G(n,\theta )}\left [ \sum _{j\ge 1} |C_j(G)|^{3} \right ]\le \frac{1}{(1-n\theta )^{3}} = \frac{1+o(1)}{\varepsilon ^3}, \end{equation}
\begin{equation} \mathbb{E}[Y^2] = \frac 1n\mathbb{E}_{G\sim \mathcal G(n,\theta )}\left [ \sum _{j\ge 1} |C_j(G)|^{3} \right ]\le \frac{1}{(1-n\theta )^{3}} = \frac{1+o(1)}{\varepsilon ^3}, \end{equation}
where the first equality is derived by averaging over the vertices and accounting for the contribution of each connected component, the inequality follows from the work of Janson and Łuczak on subcritical random graphs [Reference Janson and Luczak15], and the second equality by
![]() $1-n\theta = (1-o(1))\varepsilon$
. By assigning (3.7), (3.8), and the relations
$1-n\theta = (1-o(1))\varepsilon$
. By assigning (3.7), (3.8), and the relations
![]() $\theta \lt 1/n$
and
$\theta \lt 1/n$
and
![]() $\rho = (1+o(1))\varepsilon/n$
in (3.6), we find that
$\rho = (1+o(1))\varepsilon/n$
in (3.6), we find that
Therefore, we derive from (3.1), (3.9) and
![]() $\varepsilon ^3n\to \infty$
that
$\varepsilon ^3n\to \infty$
that
Finally, note that by Markov’s inequality,
 \begin{align*} \mathbb{P}(|\mathbb{J}|\gt \omega \varepsilon ^{-1}) \le &\, \mathbb{P}(E_c^c) + \mathbb{P}(|\mathbb{J}|\cdot \textbf{1}_{E_c}\gt \omega \varepsilon ^{-1})\\ \le &\,1-\mathbb{P}(E_c)+\frac{1+o(1)}{2\omega }. \end{align*}
\begin{align*} \mathbb{P}(|\mathbb{J}|\gt \omega \varepsilon ^{-1}) \le &\, \mathbb{P}(E_c^c) + \mathbb{P}(|\mathbb{J}|\cdot \textbf{1}_{E_c}\gt \omega \varepsilon ^{-1})\\ \le &\,1-\mathbb{P}(E_c)+\frac{1+o(1)}{2\omega }. \end{align*}
This concludes the proof using (3.5) and the assumption that
![]() $\omega \to \infty$
as
$\omega \to \infty$
as
![]() $n\to \infty$
.
$n\to \infty$
.
We now apply Lemma 3.1 to show that the
![]() $\mathcal{K}^{\infty }_{\mathrm{joint}}(\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}})$
-distributed pair
$\mathcal{K}^{\infty }_{\mathrm{joint}}(\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}})$
-distributed pair
![]() $({\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda })$
is close to
$({\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda })$
is close to
![]() $(\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda })$
, a pair of random forests that, conditioned on
$(\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda })$
, a pair of random forests that, conditioned on
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
, is
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
, is
![]() $\mathcal{K}^{\infty }(\mathbb{G}_{n,\lambda })\times \mathcal{K}^{\infty }(\mathbb{G}^\varepsilon _{n,\lambda })$
-distributed. In other words, to sample
$\mathcal{K}^{\infty }(\mathbb{G}_{n,\lambda })\times \mathcal{K}^{\infty }(\mathbb{G}^\varepsilon _{n,\lambda })$
-distributed. In other words, to sample
![]() $(\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda })$
, we first sample the pair
$(\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda })$
, we first sample the pair
![]() $(\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda })$
and then apply two independent runs of the cycle-breaking algorithm. We stress that, unconditionally,
$(\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda })$
and then apply two independent runs of the cycle-breaking algorithm. We stress that, unconditionally,
![]() $\mathbb{F}_{n,\lambda }$
and
$\mathbb{F}_{n,\lambda }$
and
![]() $\mathbb{F}^\varepsilon _{n,\lambda }$
are not independent, due to the dependence between
$\mathbb{F}^\varepsilon _{n,\lambda }$
are not independent, due to the dependence between
![]() $\mathbb{G}_{n,\lambda }$
and
$\mathbb{G}_{n,\lambda }$
and
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
. To state this claim accurately, we consider the scaled versions
$\mathbb{G}^\varepsilon _{n,\lambda }$
. To state this claim accurately, we consider the scaled versions
![]() $F_{n,\lambda }\;:\!=\;{\mathcal{S}}(\mathbb{F}_{n,\lambda })$
and
$F_{n,\lambda }\;:\!=\;{\mathcal{S}}(\mathbb{F}_{n,\lambda })$
and
![]() $F_{n,\lambda }^\varepsilon \;:\!=\;{\mathcal{S}}(\mathbb{F}_{n,\lambda })$
.
$F_{n,\lambda }^\varepsilon \;:\!=\;{\mathcal{S}}(\mathbb{F}_{n,\lambda })$
.
Lemma 3.3.
Fix
![]() $\lambda \in{\mathbb{R}}$
and let
$\lambda \in{\mathbb{R}}$
and let
![]() $\varepsilon ^3 n\to \infty$
. There exists a coupling of
$\varepsilon ^3 n\to \infty$
. There exists a coupling of
![]() $({\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda })$
and
$({\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda })$
and
![]() $(\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda })$
such that
$(\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda })$
such that
![]() ${\mathbb{M}}_{n,\lambda }=\mathbb{F}_{n,\lambda }$
and
${\mathbb{M}}_{n,\lambda }=\mathbb{F}_{n,\lambda }$
and
as
![]() $n\to \infty$
.
$n\to \infty$
.
Proof. Recall that
![]() $\mathbb{J} =\mathrm{conn}(\mathbb{G}_{n,\lambda })\cap \mathrm{conn}(\mathbb{G}^\varepsilon _{n,\lambda })$
, and
$\mathbb{J} =\mathrm{conn}(\mathbb{G}_{n,\lambda })\cap \mathrm{conn}(\mathbb{G}^\varepsilon _{n,\lambda })$
, and
![]() $\check{\mathbb{I}}=\{e\in K_n\,:\,w_e\le p,b_e=0\}$
is the random graph consists of the edges in
$\check{\mathbb{I}}=\{e\in K_n\,:\,w_e\le p,b_e=0\}$
is the random graph consists of the edges in
![]() $\mathbb{G}_{n,\lambda }\cap \mathbb{G}^\varepsilon _{n,\lambda }$
whose weight had not been resampled. We sample the graphs
$\mathbb{G}_{n,\lambda }\cap \mathbb{G}^\varepsilon _{n,\lambda }$
whose weight had not been resampled. We sample the graphs
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },{\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda }$
using
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },{\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda }$
using
![]() $W_n,W_n^\varepsilon$
(See section 2), and set
$W_n,W_n^\varepsilon$
(See section 2), and set
![]() $\mathbb{F}_{n,\lambda }\;:\!=\;{\mathbb{M}}_{n,\lambda }$
. In addition, let
$\mathbb{F}_{n,\lambda }\;:\!=\;{\mathbb{M}}_{n,\lambda }$
. In addition, let
![]() $\mathbb{F}^\varepsilon _{n,\lambda }$
be the MSF of
$\mathbb{F}^\varepsilon _{n,\lambda }$
be the MSF of
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
endowed with the following edge weights:
$\mathbb{G}^\varepsilon _{n,\lambda }$
endowed with the following edge weights:
 \begin{equation*} \tilde w_e = \begin {cases} w_e^\varepsilon & e\in \mathbb {G}^\varepsilon _{n,\lambda }\setminus (\check {\mathbb {I}}\cap \mathbb {J}), \\ p\cdot w^{\prime}_e & e\in \check {\mathbb {I}}\cap \mathbb {J}, \end {cases} \end{equation*}
\begin{equation*} \tilde w_e = \begin {cases} w_e^\varepsilon & e\in \mathbb {G}^\varepsilon _{n,\lambda }\setminus (\check {\mathbb {I}}\cap \mathbb {J}), \\ p\cdot w^{\prime}_e & e\in \check {\mathbb {I}}\cap \mathbb {J}, \end {cases} \end{equation*}
where
![]() $w^{\prime}_e$
is an independent
$w^{\prime}_e$
is an independent
![]() $\mathrm{U}[0,1]$
variable. First, we claim that the forests
$\mathrm{U}[0,1]$
variable. First, we claim that the forests
![]() $\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda }$
are retained respectively from
$\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda }$
are retained respectively from
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
by independent cycle-breaking algorithms. Namely, conditioned on
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
by independent cycle-breaking algorithms. Namely, conditioned on
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
, the pair
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
, the pair
![]() $(\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda })$
is
$(\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda })$
is
![]() $\mathcal{K}^{\infty }(\mathbb{G}_{n,\lambda })\times \mathcal{K}^{\infty }(\mathbb{G}^\varepsilon _{n,\lambda })$
-distributed. This follows from the fact that conditioned on
$\mathcal{K}^{\infty }(\mathbb{G}_{n,\lambda })\times \mathcal{K}^{\infty }(\mathbb{G}^\varepsilon _{n,\lambda })$
-distributed. This follows from the fact that conditioned on
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
and
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
and
![]() $\check{\mathbb{I}}$
, the weights
$\check{\mathbb{I}}$
, the weights
which determine the edges that are removed in the cycle-breaking algorithms, are i.i.d. Indeed, the only dependency between weights can occur via an edge from
![]() $\mathbb{J}$
but for every such an edge
$\mathbb{J}$
but for every such an edge
![]() $e$
, the weights in both graphs are independent either due to resampling (if
$e$
, the weights in both graphs are independent either due to resampling (if
![]() $e\notin \check{\mathbb{I}}$
) or by the definition of
$e\notin \check{\mathbb{I}}$
) or by the definition of
![]() $\tilde w_e$
(if
$\tilde w_e$
(if
![]() $e\in \check{\mathbb{I}}$
).
$e\in \check{\mathbb{I}}$
).
Next, we bound the distance
![]() $d_{\textrm{GHP}}^4(M_{n,\lambda }^\varepsilon,F_{n,\lambda }^\varepsilon ).$
Denote by
$d_{\textrm{GHP}}^4(M_{n,\lambda }^\varepsilon,F_{n,\lambda }^\varepsilon ).$
Denote by
![]() $B_j,\,j\ge 1$
, the event that the trees
$B_j,\,j\ge 1$
, the event that the trees
![]() $C_j({\mathbb{M}}^\varepsilon _{n,\lambda })$
and
$C_j({\mathbb{M}}^\varepsilon _{n,\lambda })$
and
![]() $C_j(\mathbb{F}^\varepsilon _{n,\lambda })$
are different. Note that the forests
$C_j(\mathbb{F}^\varepsilon _{n,\lambda })$
are different. Note that the forests
![]() ${\mathbb{M}}^\varepsilon _{n,\lambda }$
and
${\mathbb{M}}^\varepsilon _{n,\lambda }$
and
![]() $\mathbb{F}^\varepsilon _{n,\lambda }$
are retained from
$\mathbb{F}^\varepsilon _{n,\lambda }$
are retained from
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
by the cycle-breaking algorithm using, respectively, the edge weights
$\mathbb{G}^\varepsilon _{n,\lambda }$
by the cycle-breaking algorithm using, respectively, the edge weights
![]() $(w_e^\varepsilon )_{e\in \mathbb{G}^\varepsilon _{n,\lambda }}$
and
$(w_e^\varepsilon )_{e\in \mathbb{G}^\varepsilon _{n,\lambda }}$
and
![]() $(\tilde w_e)_{e\in \mathbb{G}^\varepsilon _{n,\lambda }}$
, which differ only on
$(\tilde w_e)_{e\in \mathbb{G}^\varepsilon _{n,\lambda }}$
, which differ only on
![]() $\check{\mathbb{I}}\cap \mathbb{J}$
. Therefore, if
$\check{\mathbb{I}}\cap \mathbb{J}$
. Therefore, if
![]() $B_j$
occurs then there exists a cycle
$B_j$
occurs then there exists a cycle
![]() $\gamma$
in
$\gamma$
in
![]() $C_j(\mathbb{G}^\varepsilon _{n,\lambda })$
and an edge
$C_j(\mathbb{G}^\varepsilon _{n,\lambda })$
and an edge
![]() $f\in \gamma \cap \check{\mathbb{I}}\cap \mathbb{J}$
that is the heaviest in
$f\in \gamma \cap \check{\mathbb{I}}\cap \mathbb{J}$
that is the heaviest in
![]() $\gamma$
with respect to one of the edge weights. Otherwise, the two runs of the cycle-breaking algorithms on
$\gamma$
with respect to one of the edge weights. Otherwise, the two runs of the cycle-breaking algorithms on
![]() $C_j(\mathbb{G}^\varepsilon _{n,\lambda })$
must be identical.
$C_j(\mathbb{G}^\varepsilon _{n,\lambda })$
must be identical.
Let
![]() $S$
denote the number of distinct simple cycles in
$S$
denote the number of distinct simple cycles in
![]() $C_j(\mathbb{G}^\varepsilon _{n,\lambda })$
,
$C_j(\mathbb{G}^\varepsilon _{n,\lambda })$
,
![]() $R$
the length of the shortest cycle in
$R$
the length of the shortest cycle in
![]() $C_j(\mathbb{G}^\varepsilon _{n,\lambda })$
(or
$C_j(\mathbb{G}^\varepsilon _{n,\lambda })$
(or
![]() $R=\infty$
if the component is acyclic), and let
$R=\infty$
if the component is acyclic), and let
![]() $\gamma$
be a cycle in
$\gamma$
be a cycle in
![]() $C_j(\mathbb{G}^\varepsilon _{n,\lambda })$
. Conditioned on
$C_j(\mathbb{G}^\varepsilon _{n,\lambda })$
. Conditioned on
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
and
$\mathbb{G}^\varepsilon _{n,\lambda }$
and
![]() $\mathbb{J}$
, the probability that the heaviest edge of
$\mathbb{J}$
, the probability that the heaviest edge of
![]() $\gamma$
(in each of the weights) belongs to
$\gamma$
(in each of the weights) belongs to
![]() $\mathbb{J}$
is bounded from above by
$\mathbb{J}$
is bounded from above by
![]() $|\mathbb{J}|/{R}$
, since
$|\mathbb{J}|/{R}$
, since
![]() $|\gamma |$
is bounded from below by
$|\gamma |$
is bounded from below by
![]() $R$
. Hence, by taking the union bound over all the cycles in the component and the two edge weights we find that
$R$
. Hence, by taking the union bound over all the cycles in the component and the two edge weights we find that
![]() $\mathbb{P}(B_j\,|\,\mathbb{G}^\varepsilon _{n,\lambda },\mathbb{J}) \leq 2 \cdot S \cdot |\mathbb{J}|/R.$
Therefore, for every
$\mathbb{P}(B_j\,|\,\mathbb{G}^\varepsilon _{n,\lambda },\mathbb{J}) \leq 2 \cdot S \cdot |\mathbb{J}|/R.$
Therefore, for every
![]() $\omega \gt 0$
, the probability of
$\omega \gt 0$
, the probability of
![]() $B_j$
conditioned on the event
$B_j$
conditioned on the event
![]() $C$
that
$C$
that
![]() $|\mathbb{J}|\lt \omega \varepsilon ^{-1},\,S\lt \omega,$
and
$|\mathbb{J}|\lt \omega \varepsilon ^{-1},\,S\lt \omega,$
and
![]() $R \gt n^{1/3}\omega ^{-1}$
, is bounded by
$R \gt n^{1/3}\omega ^{-1}$
, is bounded by
Consequently,
Suppose that
![]() $\omega =\omega (n)\to \infty$
as
$\omega =\omega (n)\to \infty$
as
![]() $n\to \infty$
. Lemma 3.1 asserts that first term in (3.11) is negligible. In addition, the second and third terms are also negligible by known results on critical random graphs. Namely,
$n\to \infty$
. Lemma 3.1 asserts that first term in (3.11) is negligible. In addition, the second and third terms are also negligible by known results on critical random graphs. Namely,
![]() $S$
converges in distribution to an almost-surely finite limit by [Reference Aldous5, Reference Luczak, Pittel and Wierman20], and the fact that
$S$
converges in distribution to an almost-surely finite limit by [Reference Aldous5, Reference Luczak, Pittel and Wierman20], and the fact that
![]() $n^{-1/3}\omega R$
almost surely diverges follows from [Reference Addario-Berry, Broutin and Goldschmidt3] for unicyclic components, and from [Reference Luczak, Pittel and Wierman20] for complex components (components with more than one cycle). Choosing
$n^{-1/3}\omega R$
almost surely diverges follows from [Reference Addario-Berry, Broutin and Goldschmidt3] for unicyclic components, and from [Reference Luczak, Pittel and Wierman20] for complex components (components with more than one cycle). Choosing
![]() $\omega =\omega (n)$
such that
$\omega =\omega (n)$
such that
![]() $\omega \to \infty$
and
$\omega \to \infty$
and
![]() $\omega ^3/ (\varepsilon n^{1/3})\to 0$
as
$\omega ^3/ (\varepsilon n^{1/3})\to 0$
as
![]() $n\to \infty$
results in
$n\to \infty$
results in
![]() $\mathbb{P}(B_j)\to 0$
, for every
$\mathbb{P}(B_j)\to 0$
, for every
![]() $j\geq 1$
.
$j\geq 1$
.
To complete the proof, observe that for every
![]() $\eta \gt 0$
and
$\eta \gt 0$
and
![]() $N\ge 1$
there holds
$N\ge 1$
there holds
 \begin{equation*} \mathbb{P}(d_{\textrm{GHP}}^4(M_{n,\lambda }^\varepsilon, F_{n,\lambda }^\varepsilon )\gt \eta ) \le \sum _{j=1}^{N-1} \mathbb{P}(B_j) + \mathbb{P}\left ( \sum _{j=N}^\infty d_{\textrm{GHP}}(M_{n,\lambda,j}^\varepsilon, F_{n,\lambda,j}^\varepsilon )^4 \gt \eta \right ). \end{equation*}
\begin{equation*} \mathbb{P}(d_{\textrm{GHP}}^4(M_{n,\lambda }^\varepsilon, F_{n,\lambda }^\varepsilon )\gt \eta ) \le \sum _{j=1}^{N-1} \mathbb{P}(B_j) + \mathbb{P}\left ( \sum _{j=N}^\infty d_{\textrm{GHP}}(M_{n,\lambda,j}^\varepsilon, F_{n,\lambda,j}^\varepsilon )^4 \gt \eta \right ). \end{equation*}
The first sum is negligible as
![]() $n\to \infty$
since
$n\to \infty$
since
![]() $\mathbb{P}(B_j)\to 0$
for every
$\mathbb{P}(B_j)\to 0$
for every
![]() $j\ge 1$
. In addition, by the fact that both
$j\ge 1$
. In addition, by the fact that both
![]() $M_{n,\lambda }^\varepsilon$
and
$M_{n,\lambda }^\varepsilon$
and
![]() $F_{n,\lambda }^\varepsilon$
converge in distribution as
$F_{n,\lambda }^\varepsilon$
converge in distribution as
![]() $n\to \infty$
in
$n\to \infty$
in
![]() $(\mathbb L_4,d_{\textrm{GHP}}^4)$
we have that
$(\mathbb L_4,d_{\textrm{GHP}}^4)$
we have that
 \begin{equation*} \lim _{N\to \infty }\limsup _{n\to \infty } \mathbb {P}\left ( \sum _{j=N}^\infty d_{\textrm {GHP}}(M_{n,\lambda,j}^\varepsilon, F_{n,\lambda,j}^\varepsilon )^4 \gt \eta \right )= 0, \end{equation*}
\begin{equation*} \lim _{N\to \infty }\limsup _{n\to \infty } \mathbb {P}\left ( \sum _{j=N}^\infty d_{\textrm {GHP}}(M_{n,\lambda,j}^\varepsilon, F_{n,\lambda,j}^\varepsilon )^4 \gt \eta \right )= 0, \end{equation*}
which completes the proof of the lemma.
Next, we turn to derive the asymptotic independence of the rescaled measured metric spaces
![]() $F_{n,\lambda }$
and
$F_{n,\lambda }$
and
![]() $F_{n,\lambda }^\varepsilon$
.
$F_{n,\lambda }^\varepsilon$
.
Lemma 3.4.
Fix
![]() $\lambda \in{\mathbb{R}}$
and suppose that
$\lambda \in{\mathbb{R}}$
and suppose that
![]() $\varepsilon ^3n\to \infty$
as
$\varepsilon ^3n\to \infty$
as
![]() $n\to \infty .$
Then, the pair
$n\to \infty .$
Then, the pair
![]() $(F_{n,\lambda },F_{n,\lambda }^\varepsilon )$
converges in distribution to a pair of independent copies of
$(F_{n,\lambda },F_{n,\lambda }^\varepsilon )$
converges in distribution to a pair of independent copies of
![]() $\mathscr{M}_{\lambda }$
in
$\mathscr{M}_{\lambda }$
in
![]() $(\mathbb{L}_4,d_{\textrm{GHP}}^4)$
as
$(\mathbb{L}_4,d_{\textrm{GHP}}^4)$
as
![]() $n\to \infty$
.
$n\to \infty$
.
Proof. We start by describing, in very high-level terms, how the space
![]() $\mathscr{M}_\lambda$
is constructed. Recall the random measured metric space
$\mathscr{M}_\lambda$
is constructed. Recall the random measured metric space
![]() $\mathscr{G}_\lambda$
that was introduced in refs. [Reference Addario-Berry, Broutin and Goldschmidt2], [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4], and was shown to be the limit of
$\mathscr{G}_\lambda$
that was introduced in refs. [Reference Addario-Berry, Broutin and Goldschmidt2], [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4], and was shown to be the limit of
![]() $G_{n,\lambda }$
in distribution, as
$G_{n,\lambda }$
in distribution, as
![]() $n\to \infty$
, in
$n\to \infty$
, in
![]() $(\mathbb{L}_4,d_{\textrm{GHP}}^4).$
The random space
$(\mathbb{L}_4,d_{\textrm{GHP}}^4).$
The random space
![]() $\mathscr{M}_\lambda$
was defined conditioned on
$\mathscr{M}_\lambda$
was defined conditioned on
![]() $\mathscr{G}_\lambda$
as being
$\mathscr{G}_\lambda$
as being
![]() $\mathcal{K}^{\infty }(\mathscr{G}_\lambda )$
-distributed, where
$\mathcal{K}^{\infty }(\mathscr{G}_\lambda )$
-distributed, where
![]() $\mathcal{K}^{\infty }$
is the continuous analog of the cycle-breaking algorithm.
$\mathcal{K}^{\infty }$
is the continuous analog of the cycle-breaking algorithm.
Next, denote by
![]() $(s(G_{n,\lambda,i}))_{i\geq 1}$
and
$(s(G_{n,\lambda,i}))_{i\geq 1}$
and
![]() $(s(\mathscr{G}_{\lambda,i}))_{i\geq 1}$
the sequence of surpluses of the components in
$(s(\mathscr{G}_{\lambda,i}))_{i\geq 1}$
the sequence of surpluses of the components in
![]() $G_{n,\lambda }$
and
$G_{n,\lambda }$
and
![]() $\mathscr{G}_{\lambda }$
respectively. In addition, let
$\mathscr{G}_{\lambda }$
respectively. In addition, let
![]() $(r(G_{n,\lambda,i}))_{i\geq 1}$
and
$(r(G_{n,\lambda,i}))_{i\geq 1}$
and
![]() $(r(\mathscr{G}_{\lambda,i}))_{i\geq 1}$
be the sequence of minimal length of a core edge in each component. We refer the reader to [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4] for precise definitions. The following claim follows from the proof of [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4, Theorem 4.4].
$(r(\mathscr{G}_{\lambda,i}))_{i\geq 1}$
be the sequence of minimal length of a core edge in each component. We refer the reader to [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4] for precise definitions. The following claim follows from the proof of [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4, Theorem 4.4].
Claim 3.5.
Let
![]() $\Omega$
be a probability space in which
$\Omega$
be a probability space in which
![]() $\mathbb{G}_{n,\lambda },\mathscr{G}_{\lambda }$
are commonly defined such that
$\mathbb{G}_{n,\lambda },\mathscr{G}_{\lambda }$
are commonly defined such that
![]() $\Omega$
-almost-surely there holds that
$\Omega$
-almost-surely there holds that
 \begin{align*} G_{n,\lambda }&\to \mathscr{G}_{\lambda }\mbox{ in }(\mathbb{L}_4,d_{\textrm{GHP}}^4),\\ (s(G_{n,\lambda,i}))_{i\geq 1}&\to (s(\mathscr{G}_{\lambda,i}))_{i\geq 1},\\ (r(G_{n,\lambda,i}))_{i\geq 1}&\to (r(\mathscr{G}_{\lambda,i}))_{i\geq 1}, \end{align*}
\begin{align*} G_{n,\lambda }&\to \mathscr{G}_{\lambda }\mbox{ in }(\mathbb{L}_4,d_{\textrm{GHP}}^4),\\ (s(G_{n,\lambda,i}))_{i\geq 1}&\to (s(\mathscr{G}_{\lambda,i}))_{i\geq 1},\\ (r(G_{n,\lambda,i}))_{i\geq 1}&\to (r(\mathscr{G}_{\lambda,i}))_{i\geq 1}, \end{align*}
as
![]() $n\to \infty$
. Then, for every continuity set
$n\to \infty$
. Then, for every continuity set
![]() $S$
of
$S$
of
![]() $(\mathbb{L}_4,d_{\textrm{GHP}}^4)$
for
$(\mathbb{L}_4,d_{\textrm{GHP}}^4)$
for
![]() $\mathscr{M}_\lambda$
, the convergence
$\mathscr{M}_\lambda$
, the convergence
of random variables occurs
![]() $\Omega$
-almost surely. Here, conditioned on
$\Omega$
-almost surely. Here, conditioned on
![]() $\mathbb{G}_{n,\lambda }$
and
$\mathbb{G}_{n,\lambda }$
and
![]() $\mathscr{G}_{\lambda }$
,
$\mathscr{G}_{\lambda }$
,
![]() ${\mathbb{M}}_{n,\lambda }$
is
${\mathbb{M}}_{n,\lambda }$
is
![]() $\mathcal{K}^{\infty }(\mathbb{G}_{n,\lambda })$
-distributed,
$\mathcal{K}^{\infty }(\mathbb{G}_{n,\lambda })$
-distributed,
![]() $M_{n,\lambda }\;:\!=\;{\mathcal{S}}({\mathbb{M}}_{n,\lambda })$
and
$M_{n,\lambda }\;:\!=\;{\mathcal{S}}({\mathbb{M}}_{n,\lambda })$
and
![]() $\mathscr{M}_\lambda$
is
$\mathscr{M}_\lambda$
is
![]() $\mathcal{K}^{\infty }(\mathscr{G}_\lambda )$
-distributed.
$\mathcal{K}^{\infty }(\mathscr{G}_\lambda )$
-distributed.
In fact, it is proved in ref. [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4, Theorem 4.4] that under the conditions of Claim 3.5, the cycle-breaking algorithms carried out on
![]() $\mathbb{G}_{n,\lambda },\mathscr{G}_\lambda$
can be coupled such that the convergence of
$\mathbb{G}_{n,\lambda },\mathscr{G}_\lambda$
can be coupled such that the convergence of
![]() $M_{n,\lambda }\to \mathscr{M}_{\lambda }$
in
$M_{n,\lambda }\to \mathscr{M}_{\lambda }$
in
![]() $(\mathbb{L}_4,d_{\textrm{GHP}}^4)$
also occurs
$(\mathbb{L}_4,d_{\textrm{GHP}}^4)$
also occurs
![]() $\Omega$
-almost-surely.
$\Omega$
-almost-surely.
Back to noise sensitivity, the results in refs. [Reference Lubetzky and Peled18, Theorem 2] and [Reference Frilet11, Theorem 9.1.1], establish that if
![]() $\varepsilon ^3n\to \infty$
as
$\varepsilon ^3n\to \infty$
as
![]() $n\to \infty$
then
$n\to \infty$
then
where
![]() $\mathscr{G}^{\;\prime}_\lambda$
is an independent copy of
$\mathscr{G}^{\;\prime}_\lambda$
is an independent copy of
![]() $\mathscr{G}_\lambda$
. Here the first convergence is in
$\mathscr{G}_\lambda$
. Here the first convergence is in
![]() $(\mathbb L_4,d_{\textrm{GHP}}^4)$
, and the second in the sense of finite dimensional distributions,
$(\mathbb L_4,d_{\textrm{GHP}}^4)$
, and the second in the sense of finite dimensional distributions,
The proof of [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4, Theorem 4.1] shows that this convergence can be extended to the minimal lengths of core edges, implying that
as
![]() $n\to \infty$
.
$n\to \infty$
.
Using Skorohod’s representation theorem, we may work in a probability space
![]() $\Omega$
in which the convergences. Equations (3.12),(3.13) and (3.14) occur almost surely. In addition, we can consider the distributions of
$\Omega$
in which the convergences. Equations (3.12),(3.13) and (3.14) occur almost surely. In addition, we can consider the distributions of
![]() $F_{n,\lambda },F_{n,\lambda }^\varepsilon,\mathscr{M}_\lambda$
and its independent copy
$F_{n,\lambda },F_{n,\lambda }^\varepsilon,\mathscr{M}_\lambda$
and its independent copy
![]() $\mathscr{M}^{\;\prime}_\lambda$
by constructing them via
$\mathscr{M}^{\;\prime}_\lambda$
by constructing them via
![]() $\Omega$
. Namely, conditioned on
$\Omega$
. Namely, conditioned on
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\mathscr{G}_\lambda,\mathscr{G}^{\;\prime}_\lambda$
sampled in
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\mathscr{G}_\lambda,\mathscr{G}^{\;\prime}_\lambda$
sampled in
![]() $\Omega$
, we consider the (distributions of the) following random elements:
$\Omega$
, we consider the (distributions of the) following random elements:
-
• The pair
 $(\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda })$
is
$(\mathbb{F}_{n,\lambda },\mathbb{F}^\varepsilon _{n,\lambda })$
is
 $\mathcal{K}^{\infty }(\mathbb{G}_{n,\lambda })\times \mathcal{K}^{\infty }(\mathbb{G}^\varepsilon _{n,\lambda })$
-distributed,
$\mathcal{K}^{\infty }(\mathbb{G}_{n,\lambda })\times \mathcal{K}^{\infty }(\mathbb{G}^\varepsilon _{n,\lambda })$
-distributed,
 $F_{n,\lambda }\;:\!=\;{\mathcal{S}}(\mathbb{F}_{n,\lambda })$
and
$F_{n,\lambda }\;:\!=\;{\mathcal{S}}(\mathbb{F}_{n,\lambda })$
and
 $F_{n,\lambda }^\varepsilon ={\mathcal{S}}(\mathbb{F}^\varepsilon _{n,\lambda })$
, and
$F_{n,\lambda }^\varepsilon ={\mathcal{S}}(\mathbb{F}^\varepsilon _{n,\lambda })$
, and -
• The pair
 $(\mathscr{M}_\lambda,\mathscr{M}^{\;\prime}_\lambda)$
is
$(\mathscr{M}_\lambda,\mathscr{M}^{\;\prime}_\lambda)$
is
 $\mathcal{K}^{\infty }(\mathscr{G}_\lambda ) \times \mathcal{K}^{\infty }(\mathscr{G}^{\;\prime}_\lambda)$
-distributed.
$\mathcal{K}^{\infty }(\mathscr{G}_\lambda ) \times \mathcal{K}^{\infty }(\mathscr{G}^{\;\prime}_\lambda)$
-distributed.
We observe that the pair
![]() $(F_{n,\lambda },F_{n,\lambda }^\varepsilon )$
is conditionally independent given
$(F_{n,\lambda },F_{n,\lambda }^\varepsilon )$
is conditionally independent given
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
, and the pair
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
, and the pair
![]() $(\mathscr{M}_\lambda,\mathscr{M}^{\;\prime}_\lambda)$
is independent and identically distributed.
$(\mathscr{M}_\lambda,\mathscr{M}^{\;\prime}_\lambda)$
is independent and identically distributed.
Our goal is to show that for every continuity sets
![]() $S,S'$
of
$S,S'$
of
![]() $(\mathbb L_4,d_{\textrm{GHP}}^4)$
for the distribution of
$(\mathbb L_4,d_{\textrm{GHP}}^4)$
for the distribution of
![]() $\mathscr{M}_\lambda$
there holds
$\mathscr{M}_\lambda$
there holds
as
![]() $n\to \infty$
.
$n\to \infty$
.
Note that by our assumption on the almost-sure convergences in
![]() $\Omega$
, we can apply Claim 3.5 twice and obtain that for every two such continuity sets
$\Omega$
, we can apply Claim 3.5 twice and obtain that for every two such continuity sets
![]() $S,S'$
there holds that both convergences
$S,S'$
there holds that both convergences
and
occur
![]() $\Omega$
-almost surely. Consequently, the proof is concluded as follows:
$\Omega$
-almost surely. Consequently, the proof is concluded as follows:
 \begin{align*} \mathbb{P}(F_{n,\lambda }\in S,F^\varepsilon _{n,\lambda }\in S')&=\, \mathbb{E}[\mathbb{P}(F_{n,\lambda }\in S,F^\varepsilon _{n,\lambda }\in S'\,|\,\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda })]\\ &=\, \mathbb{E}[\mathbb{P}(F_{n,\lambda }\in S \,|\,\mathbb{G}_{n,\lambda })\cdot \mathbb{P}(F_{n,\lambda }^\varepsilon \in S' \,|\,\mathbb{G}^\varepsilon _{n,\lambda })]\\ &\to \, \mathbb{E}[\mathbb{P}(\mathscr{M}_\lambda \in S \,|\,\mathscr{G}_\lambda )\cdot \mathbb{P}(\mathscr{M}^{\;\prime}_\lambda\in S' \,|\,\mathscr{G}^{\;\prime}_\lambda)]\\ &=\, \mathbb{E}[\mathbb{P}(\mathscr{M}_\lambda \in S \,|\,\mathscr{G}_\lambda )]\cdot \mathbb{E}[\mathbb{P}(\mathscr{M}^{\;\prime}_\lambda\in S' \,|\,\mathscr{G}^{\;\prime}_\lambda)]\\ &=\,\mathbb{P}(\mathscr{M}_\lambda \in S)\cdot \mathbb{P}(\mathscr{M}^{\;\prime}_\lambda\in S'). \end{align*}
\begin{align*} \mathbb{P}(F_{n,\lambda }\in S,F^\varepsilon _{n,\lambda }\in S')&=\, \mathbb{E}[\mathbb{P}(F_{n,\lambda }\in S,F^\varepsilon _{n,\lambda }\in S'\,|\,\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda })]\\ &=\, \mathbb{E}[\mathbb{P}(F_{n,\lambda }\in S \,|\,\mathbb{G}_{n,\lambda })\cdot \mathbb{P}(F_{n,\lambda }^\varepsilon \in S' \,|\,\mathbb{G}^\varepsilon _{n,\lambda })]\\ &\to \, \mathbb{E}[\mathbb{P}(\mathscr{M}_\lambda \in S \,|\,\mathscr{G}_\lambda )\cdot \mathbb{P}(\mathscr{M}^{\;\prime}_\lambda\in S' \,|\,\mathscr{G}^{\;\prime}_\lambda)]\\ &=\, \mathbb{E}[\mathbb{P}(\mathscr{M}_\lambda \in S \,|\,\mathscr{G}_\lambda )]\cdot \mathbb{E}[\mathbb{P}(\mathscr{M}^{\;\prime}_\lambda\in S' \,|\,\mathscr{G}^{\;\prime}_\lambda)]\\ &=\,\mathbb{P}(\mathscr{M}_\lambda \in S)\cdot \mathbb{P}(\mathscr{M}^{\;\prime}_\lambda\in S'). \end{align*}
The first equality holds by the law of total expectation, and the second equality is due to the conditional independence of
![]() $F_{n,\lambda },F_{n,\lambda }^\varepsilon$
given
$F_{n,\lambda },F_{n,\lambda }^\varepsilon$
given
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
. The convergence, which occurs as
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
. The convergence, which occurs as
![]() $n\to \infty$
, is obtained from the
$n\to \infty$
, is obtained from the
![]() $\Omega$
-almost-sure convergences (3.15), (3.16) and using the dominated convergence theorem. The next equality is obtained by the independence of
$\Omega$
-almost-sure convergences (3.15), (3.16) and using the dominated convergence theorem. The next equality is obtained by the independence of
![]() $\mathscr{G}_\lambda$
,
$\mathscr{G}_\lambda$
,
![]() $\mathscr{G}^{\;\prime}_\lambda$
which is where the noise sensitivity of the measured metric structure of
$\mathscr{G}^{\;\prime}_\lambda$
which is where the noise sensitivity of the measured metric structure of
![]() $\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
is being used. The last equality follows from the law of total expectation.
$\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda }$
is being used. The last equality follows from the law of total expectation.
We conclude this subsection with a proof of the noise sensitivity of the MSF of
![]() $\mathbb{G}_{n,\lambda }$
, which we derive from the following well-known theorem.
$\mathbb{G}_{n,\lambda }$
, which we derive from the following well-known theorem.
Theorem 3.6 ([Reference Billingsley8, Theorem 3.1]). Let
![]() $S$
be a Polish space with metric
$S$
be a Polish space with metric
![]() $\rho$
and
$\rho$
and
![]() $(X_n,Y_n)$
be random elements of
$(X_n,Y_n)$
be random elements of
![]() $S\times S$
. If
$S\times S$
. If
![]() $\,Y_n\xrightarrow{\,\mathrm{d}\,} X$
and
$\,Y_n\xrightarrow{\,\mathrm{d}\,} X$
and
![]() $\rho (X_n,Y_n)\xrightarrow{\,\mathrm{p}\,} 0$
as
$\rho (X_n,Y_n)\xrightarrow{\,\mathrm{p}\,} 0$
as
![]() $n\to \infty$
, then
$n\to \infty$
, then
![]() $X_n\xrightarrow{\,\mathrm{d}\,} X$
.
$X_n\xrightarrow{\,\mathrm{d}\,} X$
.
Proof of Theorem
1.2, Part (1). Denote the polish metric space
![]() $S=(\mathbb L_4,d_{\textrm{GHP}}^4)^2$
endowed with some product metric
$S=(\mathbb L_4,d_{\textrm{GHP}}^4)^2$
endowed with some product metric
![]() $\rho$
. Suppose that the random elements
$\rho$
. Suppose that the random elements
are sampled via the coupling from Lemma 3.3. Lemma 3.4 asserts that
![]() $(F_{n,\lambda },F_{n,\lambda }^\varepsilon )$
converges in distribution to a pair of independent copies of
$(F_{n,\lambda },F_{n,\lambda }^\varepsilon )$
converges in distribution to a pair of independent copies of
![]() $\mathscr{M}_{\lambda }$
. In addition, by Lemma 3.3,
$\mathscr{M}_{\lambda }$
. In addition, by Lemma 3.3,
as
![]() $n\to \infty$
. Consequently, we derive from Theorem 3.6 that
$n\to \infty$
. Consequently, we derive from Theorem 3.6 that
![]() $(M_{n,\lambda },M_{n,\lambda }^\varepsilon )$
converges in distribution to a pair of independent copies of
$(M_{n,\lambda },M_{n,\lambda }^\varepsilon )$
converges in distribution to a pair of independent copies of
![]() $\mathscr{M}_{\lambda }$
, as claimed.
$\mathscr{M}_{\lambda }$
, as claimed.
3.2 Noise stability of the MSF
We now assume that
![]() $\varepsilon ^3n\to 0$
as
$\varepsilon ^3n\to 0$
as
![]() $n\to \infty$
. In this case, the noise stability of the MSF follows from the similarity between the cycle-breaking algorithms. Namely, the
$n\to \infty$
. In this case, the noise stability of the MSF follows from the similarity between the cycle-breaking algorithms. Namely, the
![]() $\mathcal{K}^{\infty }_{\mathrm{joint}}(\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}})$
-distributed pair
$\mathcal{K}^{\infty }_{\mathrm{joint}}(\mathbb{G}_{n,\lambda },\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}})$
-distributed pair
![]() $({\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda })$
is obtained by removing the exact same set of edges from both graphs. We derive this from the following claim which asserts that all the cycles in
$({\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda })$
is obtained by removing the exact same set of edges from both graphs. We derive this from the following claim which asserts that all the cycles in
![]() $\mathbb{G}_{n,\lambda }$
and
$\mathbb{G}_{n,\lambda }$
and
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
appear in their common subgraph
$\mathbb{G}^\varepsilon _{n,\lambda }$
appear in their common subgraph
![]() $\check{\mathbb{I}}$
consisting of the edges whose weight was not resampled.
$\check{\mathbb{I}}$
consisting of the edges whose weight was not resampled.
Claim 3.7.
Let
![]() $\lambda \in{\mathbb{R}}$
,
$\lambda \in{\mathbb{R}}$
,
![]() $j\geq 1$
,
$j\geq 1$
,
![]() $\varepsilon ^3 n \to 0$
, and
$\varepsilon ^3 n \to 0$
, and
![]() $\mathbb{G}_{n,\lambda }$
and
$\mathbb{G}_{n,\lambda }$
and
![]() $\check{\mathbb{I}}$
defined as in section
2.1
. Let
$\check{\mathbb{I}}$
defined as in section
2.1
. Let
![]() $B_j$
denote the event that
$B_j$
denote the event that
![]() $\mathrm{conn}(C_j(\mathbb{G}_{n,\lambda })) =\mathrm{conn}(C_j(\check{\mathbb{I}}))$
. Then,
$\mathrm{conn}(C_j(\mathbb{G}_{n,\lambda })) =\mathrm{conn}(C_j(\check{\mathbb{I}}))$
. Then,
![]() $\mathbb{P}(B_j)\to 1$
as
$\mathbb{P}(B_j)\to 1$
as
![]() $n\to \infty$
.
$n\to \infty$
.
Proof. We observe that conditioned on
![]() $\mathbb{G}_{n,\lambda }$
, the graph
$\mathbb{G}_{n,\lambda }$
, the graph
![]() $\check{\mathbb{I}}$
is obtained from
$\check{\mathbb{I}}$
is obtained from
![]() $\mathbb{G}_{n,\lambda }$
by removing each edge independently with probability
$\mathbb{G}_{n,\lambda }$
by removing each edge independently with probability
![]() $\varepsilon$
. Therefore, by [Reference Lubetzky and Peled18, Lemma 5.4], the event
$\varepsilon$
. Therefore, by [Reference Lubetzky and Peled18, Lemma 5.4], the event
![]() $A_j$
that
$A_j$
that
![]() $C_j(\check{\mathbb{I}})\subseteq C_j(\mathbb{G}_{n,\lambda })$
occurs with probability tending to
$C_j(\check{\mathbb{I}})\subseteq C_j(\mathbb{G}_{n,\lambda })$
occurs with probability tending to
![]() $1$
as
$1$
as
![]() $n\to \infty .$
In addition, under the event
$n\to \infty .$
In addition, under the event
![]() $A_j$
, the event
$A_j$
, the event
![]() $B_j$
does not occur only if there exists an edge
$B_j$
does not occur only if there exists an edge
![]() $e\in \mathrm{conn}(C_j(\mathbb{G}_{n,\lambda }))$
that
$e\in \mathrm{conn}(C_j(\mathbb{G}_{n,\lambda }))$
that
![]() $\check{\mathbb{I}}$
did not retain. Therefore, for every
$\check{\mathbb{I}}$
did not retain. Therefore, for every
![]() $\omega =\omega (n)\gt 0$
,
$\omega =\omega (n)\gt 0$
,
where the second term bounds the expected number of edges from
![]() $\mathrm{conn}(\mathbb{G}_{n,\lambda })$
that
$\mathrm{conn}(\mathbb{G}_{n,\lambda })$
that
![]() $\check{\mathbb{I}}$
did not retain, conditioned on
$\check{\mathbb{I}}$
did not retain, conditioned on
![]() $|\mathrm{conn}(C_j(\mathbb{G}_{n,\lambda }))|\le \omega n^{1/3}$
. We derive the claim by combining
$|\mathrm{conn}(C_j(\mathbb{G}_{n,\lambda }))|\le \omega n^{1/3}$
. We derive the claim by combining
![]() $\mathbb{P}(A_j)\to 1$
and assigning in (3.17) a sequence
$\mathbb{P}(A_j)\to 1$
and assigning in (3.17) a sequence
![]() $\omega = \omega (n)$
such that
$\omega = \omega (n)$
such that
![]() $\omega \to \infty$
and
$\omega \to \infty$
and
![]() $\varepsilon \omega n^{1/3}\to 0$
as
$\varepsilon \omega n^{1/3}\to 0$
as
![]() $n\to \infty$
. Indeed, in such a case we have that
$n\to \infty$
. Indeed, in such a case we have that
![]() $\mathbb{P}(n^{-1/3}|\mathrm{conn}(C_j(\mathbb{G}_{n,\lambda }))|\gt \omega )\to 0$
, since the maximum number of cycles in
$\mathbb{P}(n^{-1/3}|\mathrm{conn}(C_j(\mathbb{G}_{n,\lambda }))|\gt \omega )\to 0$
, since the maximum number of cycles in
![]() $\mathbb{G}_{n,\lambda }$
is bounded in probability [Reference Luczak, Pittel and Wierman20], and so is the length of the largest cycle in
$\mathbb{G}_{n,\lambda }$
is bounded in probability [Reference Luczak, Pittel and Wierman20], and so is the length of the largest cycle in
![]() $C_j(\mathbb{G}_{n,\lambda })$
divided by
$C_j(\mathbb{G}_{n,\lambda })$
divided by
![]() $n^{1/3}$
[Reference Addario-Berry, Broutin and Goldschmidt3, Reference Luczak, Pittel and Wierman20].
$n^{1/3}$
[Reference Addario-Berry, Broutin and Goldschmidt3, Reference Luczak, Pittel and Wierman20].
Note that the assertion in Claim 3.7 also holds for
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
since
$\mathbb{G}^\varepsilon _{n,\lambda }$
since
![]() $(\mathbb{G}_{n,\lambda },\check{\mathbb{I}})\stackrel{d}{=}(\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}})$
. We now turn to conclude the proof of Theorem 1.2.
$(\mathbb{G}_{n,\lambda },\check{\mathbb{I}})\stackrel{d}{=}(\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}})$
. We now turn to conclude the proof of Theorem 1.2.
Proof of Theorem
1.2 Part 2. Denote by
![]() $\check{\mathbb{M}}$
the MSF of the graph
$\check{\mathbb{M}}$
the MSF of the graph
![]() $\check{\mathbb{I}}$
endowed with the edge weights from
$\check{\mathbb{I}}$
endowed with the edge weights from
![]() $W_n$
, and let
$W_n$
, and let
![]() $\check M\;:\!=\;{\mathcal{S}}(\check{\mathbb{M}})$
. First, we argue that for every fixed
$\check M\;:\!=\;{\mathcal{S}}(\check{\mathbb{M}})$
. First, we argue that for every fixed
![]() $j \ge 1$
,
$j \ge 1$
,
as
![]() $n\to \infty$
. By Claim 3.7, we can condition on the event
$n\to \infty$
. By Claim 3.7, we can condition on the event
![]() $B_j$
. Under this event, the joint cycle-breaking algorithm running on
$B_j$
. Under this event, the joint cycle-breaking algorithm running on
![]() $C_j(\mathbb{G}_{n,\lambda })$
and
$C_j(\mathbb{G}_{n,\lambda })$
and
![]() $C_j(\check{\mathbb{I}})$
removes the same edges in both graphs. Since
$C_j(\check{\mathbb{I}})$
removes the same edges in both graphs. Since
![]() $\check{\mathbb{I}}$
is a subgraph of
$\check{\mathbb{I}}$
is a subgraph of
![]() $\mathbb{G}_{n,\lambda }$
, we deduce that
$\mathbb{G}_{n,\lambda }$
, we deduce that
![]() $C_j({\mathbb{M}}_{n,\lambda })$
is obtained from
$C_j({\mathbb{M}}_{n,\lambda })$
is obtained from
![]() $C_j(\check{\mathbb{M}})$
by the addition of the forest
$C_j(\check{\mathbb{M}})$
by the addition of the forest
![]() $C_j(\mathbb{G}_{n,\lambda }) \setminus C_j(\check{\mathbb{I}})$
. We derive (3.18) by the proof of [Reference Lubetzky and Peled18, Theorem 2], which shows that with probability tending to
$C_j(\mathbb{G}_{n,\lambda }) \setminus C_j(\check{\mathbb{I}})$
. We derive (3.18) by the proof of [Reference Lubetzky and Peled18, Theorem 2], which shows that with probability tending to
![]() $1$
as
$1$
as
![]() $n\to \infty$
, the graph
$n\to \infty$
, the graph
![]() $C_j(\mathbb{G}_{n,\lambda })$
is contained in a neighbourhood of radius
$C_j(\mathbb{G}_{n,\lambda })$
is contained in a neighbourhood of radius
![]() $o(n^{1/3})$
around
$o(n^{1/3})$
around
![]() $C_j(\check{\mathbb{I}})$
, and that the two graphs differ by
$C_j(\check{\mathbb{I}})$
, and that the two graphs differ by
![]() $o(n^{2/3})$
vertices.
$o(n^{2/3})$
vertices.
Since
![]() $(\mathbb{G}_{n,\lambda },\check{\mathbb{I}},W_n)\stackrel{d}{=}(\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}},W_n^\varepsilon )$
, we can use the same argument for
$(\mathbb{G}_{n,\lambda },\check{\mathbb{I}},W_n)\stackrel{d}{=}(\mathbb{G}^\varepsilon _{n,\lambda },\check{\mathbb{I}},W_n^\varepsilon )$
, we can use the same argument for
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
instead of
$\mathbb{G}^\varepsilon _{n,\lambda }$
instead of
![]() $\mathbb{G}_{n,\lambda }$
, and find that
$\mathbb{G}_{n,\lambda }$
, and find that
as
![]() $n\to \infty$
. To conclude Theorem 1.2 Part 2 we need to extend the component-wise convergence to
$n\to \infty$
. To conclude Theorem 1.2 Part 2 we need to extend the component-wise convergence to
![]() $\left (\mathbb{L}_4,d_{GHP}^4\right )$
. This is carried out exactly as in the proof of Lemma 3.3, following [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4, Theorems 4.1, 4.4].
$\left (\mathbb{L}_4,d_{GHP}^4\right )$
. This is carried out exactly as in the proof of Lemma 3.3, following [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4, Theorems 4.1, 4.4].
4. Proof of Theorem 1.1
The connection between the scaling limits of the MST
![]() ${\mathbb{M}}_n$
and the largest component of the MSF
${\mathbb{M}}_n$
and the largest component of the MSF
![]() ${\mathbb{M}}_{n,\lambda }$
was established in [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4, Proposition 4.8]. Let
${\mathbb{M}}_{n,\lambda }$
was established in [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4, Proposition 4.8]. Let
![]() $M_n = \hat{{\mathcal{S}}}({\mathbb{M}}_{n,\lambda })$
and
$M_n = \hat{{\mathcal{S}}}({\mathbb{M}}_{n,\lambda })$
and
![]() $\hat{M}_{n,\lambda,1} = \hat{{\mathcal{S}}}({\mathbb{M}}_{n,\lambda,1})$
(see section 2.1). Then, for every
$\hat{M}_{n,\lambda,1} = \hat{{\mathcal{S}}}({\mathbb{M}}_{n,\lambda,1})$
(see section 2.1). Then, for every
![]() $\eta \gt 0$
,
$\eta \gt 0$
,
and a similar statement holds for
![]() $M_n^\varepsilon,\hat{M}_{n,\lambda,1}^\varepsilon$
.
$M_n^\varepsilon,\hat{M}_{n,\lambda,1}^\varepsilon$
.
In addition, let
![]() $\;\;\;\hat{\!\!\!\mathscr{M}}_{\lambda,1}$
be the measured metric space obtained from the scaling limit
$\;\;\;\hat{\!\!\!\mathscr{M}}_{\lambda,1}$
be the measured metric space obtained from the scaling limit
![]() $\mathscr{M}_{\lambda,1}$
by renormalizing its measure to a probability measure. The so-called principle of accompanying laws [Reference Stroock25, Theorem 9.1.13] yields that
$\mathscr{M}_{\lambda,1}$
by renormalizing its measure to a probability measure. The so-called principle of accompanying laws [Reference Stroock25, Theorem 9.1.13] yields that
![]() $M_n \xrightarrow{\,\mathrm{d}\,} \mathscr{M}$
in
$M_n \xrightarrow{\,\mathrm{d}\,} \mathscr{M}$
in
![]() $(\mathcal{M},d_{\textrm{GHP}})$
, where the random measured metric space
$(\mathcal{M},d_{\textrm{GHP}})$
, where the random measured metric space
![]() $\mathscr{M}$
is the limit of
$\mathscr{M}$
is the limit of
![]() $\;\;\;\hat{\!\!\!\mathscr{M}}_{\lambda,1} \xrightarrow{\,\mathrm{d}\,} \mathscr{M}$
in
$\;\;\;\hat{\!\!\!\mathscr{M}}_{\lambda,1} \xrightarrow{\,\mathrm{d}\,} \mathscr{M}$
in
![]() $d_{\textrm{GHP}}$
as
$d_{\textrm{GHP}}$
as
![]() $n\to \infty$
. Given this background, Theorem 1.1 follows directly from Theorem 1.2.
$n\to \infty$
. Given this background, Theorem 1.1 follows directly from Theorem 1.2.
Proof of Theorem
1.1. For Part 1, we let
![]() $\rho$
be some product metric on
$\rho$
be some product metric on
![]() $(\mathcal{M},d_{\textrm{GHP}})^2$
, and deduce from (4.1) that for every
$(\mathcal{M},d_{\textrm{GHP}})^2$
, and deduce from (4.1) that for every
![]() $\eta \gt 0,$
$\eta \gt 0,$
In addition, Theorem 1.1 Part 1 implies that
in
![]() $(\mathcal{M},d_{\textrm{GHP}})^2$
, as
$(\mathcal{M},d_{\textrm{GHP}})^2$
, as
![]() $n\to \infty$
. Let
$n\to \infty$
. Let
![]() $\;\;\;\hat{\!\!\!\mathscr{M}}^{\;\prime}_{\lambda,1}$
to be an independent copy of
$\;\;\;\hat{\!\!\!\mathscr{M}}^{\;\prime}_{\lambda,1}$
to be an independent copy of
![]() $\;\;\;\hat{\!\!\!\mathscr{M}}_{\lambda,1}$
, hence
$\;\;\;\hat{\!\!\!\mathscr{M}}_{\lambda,1}$
, hence
as
![]() $\lambda \to \infty$
in
$\lambda \to \infty$
in
![]() $d_{\textrm{GHP}}$
, where
$d_{\textrm{GHP}}$
, where
![]() $\mathscr{M}$
and
$\mathscr{M}$
and
![]() $\mathscr{M}^{\;\prime}$
are i.i.d. Therefore, by the principle of accompanying laws, as
$\mathscr{M}^{\;\prime}$
are i.i.d. Therefore, by the principle of accompanying laws, as
![]() $n\to \infty$
, the pair
$n\to \infty$
, the pair
![]() $(M_n,M_n^\varepsilon )\xrightarrow{\,\mathrm{d}\,}\left (\mathscr{M},\mathscr{M}^{\;\prime}\right )$
in
$(M_n,M_n^\varepsilon )\xrightarrow{\,\mathrm{d}\,}\left (\mathscr{M},\mathscr{M}^{\;\prime}\right )$
in
![]() $d_{\textrm{GHP}}$
.
$d_{\textrm{GHP}}$
.
For Part 2, note that for every
![]() $\eta \gt 0$
and every
$\eta \gt 0$
and every
![]() $\lambda \in{\mathbb{R}}$
there holds
$\lambda \in{\mathbb{R}}$
there holds
where
![]() $D_1,D_2$
and
$D_1,D_2$
and
![]() $D_3$
are the events that the GHP distance between
$D_3$
are the events that the GHP distance between
![]() $ \left (M_n,\hat{M}_{n,\lambda,1}\right )$
,
$ \left (M_n,\hat{M}_{n,\lambda,1}\right )$
,
![]() $\left (M_n^\varepsilon,\hat{M}_{n,\lambda,1}^\varepsilon \right )$
and
$\left (M_n^\varepsilon,\hat{M}_{n,\lambda,1}^\varepsilon \right )$
and
![]() $\left (\hat{M}_{n,\lambda,1},\hat{M}^\varepsilon _{n,\lambda,1}\right )$
is greater than
$\left (\hat{M}_{n,\lambda,1},\hat{M}^\varepsilon _{n,\lambda,1}\right )$
is greater than
![]() $\eta/3$
, respectively.
$\eta/3$
, respectively.
Part 2 of Theorem 1.2 implies that
![]() $ d_{\textrm{GHP}}\left (\hat{M}_{n,\lambda,1},\hat{M}^\varepsilon _{n,\lambda,1}\right )\xrightarrow{\,\mathrm{p}\,} 0$
as
$ d_{\textrm{GHP}}\left (\hat{M}_{n,\lambda,1},\hat{M}^\varepsilon _{n,\lambda,1}\right )\xrightarrow{\,\mathrm{p}\,} 0$
as
![]() $n\to \infty$
, thereby
$n\to \infty$
, thereby
![]() $\mathbb{P}(D_3)\to 0$
. By applying (4.1) to both
$\mathbb{P}(D_3)\to 0$
. By applying (4.1) to both
![]() $ \left (M_n,\hat{M}_{n,\lambda,1}\right )$
and
$ \left (M_n,\hat{M}_{n,\lambda,1}\right )$
and
![]() $ \left (M_n^\varepsilon,\hat{M}_{n,\lambda,1}^\varepsilon \right )$
, we find that
$ \left (M_n^\varepsilon,\hat{M}_{n,\lambda,1}^\varepsilon \right )$
, we find that
therefore
![]() $\mathbb{P}(d_{\textrm{GHP}}(M_n,M_n^\varepsilon )\gt \eta ) \to 0$
as
$\mathbb{P}(d_{\textrm{GHP}}(M_n,M_n^\varepsilon )\gt \eta ) \to 0$
as
![]() $n\to \infty$
, as claimed.
$n\to \infty$
, as claimed.
5. Open problems
We conclude with three open problems that naturally arise from our work. First, it will be interesting to study the joint limit law of the scaled MSTs
![]() $(M_n,M_n^\varepsilon )$
and of the scaled MSFs
$(M_n,M_n^\varepsilon )$
and of the scaled MSFs
![]() $(M_{n,\lambda },M_{n,\lambda }^\varepsilon )$
in the critical noise regime
$(M_{n,\lambda },M_{n,\lambda }^\varepsilon )$
in the critical noise regime
![]() $\varepsilon = tn^{-1/3},\,t\in{\mathbb{R}}$
. Rossignol [Reference Rossignol24] identified a non-trivial correlation between
$\varepsilon = tn^{-1/3},\,t\in{\mathbb{R}}$
. Rossignol [Reference Rossignol24] identified a non-trivial correlation between
![]() $\mathbb{G}_{n,\lambda }$
and
$\mathbb{G}_{n,\lambda }$
and
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
, but we suspect that the correlations between the MSFs are even more involved. Namely, in this regime the subgraphs
$\mathbb{G}^\varepsilon _{n,\lambda }$
, but we suspect that the correlations between the MSFs are even more involved. Namely, in this regime the subgraphs
![]() $\mathrm{conn}(\mathbb{G}_{n,\lambda })$
and
$\mathrm{conn}(\mathbb{G}_{n,\lambda })$
and
![]() $\mathrm{conn}(\mathbb{G}^\varepsilon _{n,\lambda })$
share a positive fraction of their weighted edges. Hence, on top of the correlations between
$\mathrm{conn}(\mathbb{G}^\varepsilon _{n,\lambda })$
share a positive fraction of their weighted edges. Hence, on top of the correlations between
![]() $\mathbb{G}_{n,\lambda }$
and
$\mathbb{G}_{n,\lambda }$
and
![]() $\mathbb{G}^\varepsilon _{n,\lambda }$
, the joint cycle-breaking algorithm retaining
$\mathbb{G}^\varepsilon _{n,\lambda }$
, the joint cycle-breaking algorithm retaining
![]() ${\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda }$
is also non-trivially correlated.
${\mathbb{M}}_{n,\lambda },{\mathbb{M}}^\varepsilon _{n,\lambda }$
is also non-trivially correlated.
Second, even though this paper considers
![]() $\mathrm{U}[0,1]$
-distributed weights, our setting can be equivalently described in discrete terms. It is also natural to consider similar problems in a continuous noise model, e.g., by letting
$\mathrm{U}[0,1]$
-distributed weights, our setting can be equivalently described in discrete terms. It is also natural to consider similar problems in a continuous noise model, e.g., by letting
![]() $(w_e,w_e^\varepsilon )$
be identically distributed normal variables with covariance
$(w_e,w_e^\varepsilon )$
be identically distributed normal variables with covariance
![]() $\varepsilon$
. We ask: what is the sensitivity-stability noise threshold of the scaled MST in this model? is it still aligned with the critical window of the Erdős-Rényi random graphs?
$\varepsilon$
. We ask: what is the sensitivity-stability noise threshold of the scaled MST in this model? is it still aligned with the critical window of the Erdős-Rényi random graphs?
Third, it is interesting to explore for which functions of the MST our theorem establishes noise sensitivity and stability. This requires a better understanding of the limit
![]() $\mathscr{M}$
and its continuity sets. For example, consider the diameter of
$\mathscr{M}$
and its continuity sets. For example, consider the diameter of
![]() $\mathscr{M}$
or the distance between two independent random points in it. Are these random variables continuous? What are their support? It is not entirely clear to us how to answer these questions using the construction in ref. [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4] of
$\mathscr{M}$
or the distance between two independent random points in it. Are these random variables continuous? What are their support? It is not entirely clear to us how to answer these questions using the construction in ref. [Reference Addario-Berry, Broutin, Goldschmidt and Miermont4] of
![]() $\mathscr{M}$
as the limit of
$\mathscr{M}$
as the limit of
![]() $\mathscr{M}_{\lambda }$
as
$\mathscr{M}_{\lambda }$
as
![]() $\lambda \to \infty$
. However, it appears that the recent explicit construction of
$\lambda \to \infty$
. However, it appears that the recent explicit construction of
![]() $\mathscr{M}$
as the Brownian parabolic tree [Reference Broutin and Marckert9] can be quite useful here.
$\mathscr{M}$
as the Brownian parabolic tree [Reference Broutin and Marckert9] can be quite useful here.
Acknowledgements
We thank the anonymous referee for their very helpful comments and suggestions.