Research Article
On the Minimum Order of Graphs with Given Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 467-470
-
- Article
-
- You have access
- Export citation
On Cayley-Dickson Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 625-627
-
- Article
-
- You have access
- Export citation
The Local Growth of Power Series: A Survey of the Wiman-Valiron Method
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 317-358
-
- Article
-
- You have access
- Export citation
The Influence on a Finite Group of its Permutable Subgroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 159-165
-
- Article
-
- You have access
- Export citation
Rings with A Finitely Generated Total Quotient Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-4
-
- Article
-
- You have access
- Export citation
On the Levitzki Radical
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 5-10
-
- Article
-
- You have access
- Export citation
Tauberian Theorems for Borel-Type Methods of Summability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 167-173
-
- Article
-
- You have access
- Export citation
Sequences Realizable by Graphs with Hamiltonian Squares
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 629-631
-
- Article
-
- You have access
- Export citation
On Permutation Groups with Regular Subgroup
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 359-361
-
- Article
-
- You have access
- Export citation
Model Theory of Epimorphisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 471-477
-
- Article
-
- You have access
- Export citation
Equational Compactness of G-Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 11-18
-
- Article
-
- You have access
- Export citation
On Pure-High Subgroups of Abelian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 479-482
-
- Article
-
- You have access
- Export citation
Right-Ordered Polycyclic Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 175-178
-
- Article
-
- You have access
- Export citation
Adjoints of a Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 363-365
-
- Article
-
- You have access
- Export citation
Synchronous and Asynchronous Reversible Markov Systems(1)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 633-649
-
- Article
-
- You have access
- Export citation
The Matrix Equations A = XYZ And B = ZYX and Related Ones
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 179-183
-
- Article
-
- You have access
- Export citation
Vector Bundles Over Suspensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 483-484
-
- Article
-
- You have access
- Export citation
On Regulating Sets and the Disparity of Planar Cubic Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 367-374
-
- Article
-
- You have access
- Export citation
On the Complete Regularity of Some Category Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 651-656
-
- Article
-
- You have access
- Export citation
Complementarity Problem and Duality Over Convex Cones
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 19-25
-
- Article
-
- You have access
- Export citation



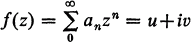

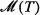 be the category of models of
be the category of models of