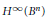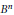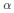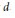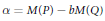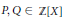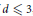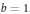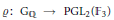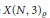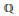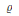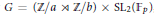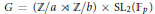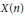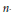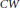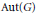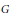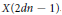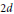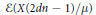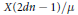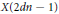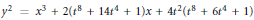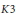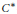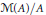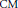Research Article
Functoriality of the Coniveau Filtration
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 161-171
-
- Article
-
- You have access
- Export citation
An Infinite Dimensional Vector Space of Universal Functions for H∞ of the Ball
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 172-181
-
- Article
-
- You have access
- Export citation
On the Coxeter Transformations for Tamari Posets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 182-190
-
- Article
-
- You have access
- Export citation
Every Real Algebraic Integer Is a Difference of Two Mahler Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 191-195
-
- Article
-
- You have access
- Export citation
Plane Quartic Twists of X(5, 3)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 196-205
-
- Article
-
- You have access
- Export citation
Spherical Space Forms: Homotopy Types and Self-Equivalences for the Group (ℤ/a ⋊ ℤ/b) × SL2 (
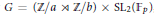 p)
p)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 206-214
-
- Article
-
- You have access
- Export citation
Elliptic K3 Surfaces with Geometric Mordell–Weil Rank 15
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 215-226
-
- Article
-
- You have access
- Export citation
AF-Skeletons and Real Rank Zero Algebras with the Corona Factorization Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 227-233
-
- Article
-
- You have access
- Export citation
A Remark on a Modular Analogue of the Sato–Tate Conjecture
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 234-242
-
- Article
-
- You have access
- Export citation
Un nouveau point de repère dans la théorie des formes automorphes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 243-267
-
- Article
-
- You have access
- Export citation
Award Winners
Research Article
On the Lack of Inverses to C*-Extensions Related to Property T Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 268-283
-
- Article
-
- You have access
- Export citation
Research Article
Second Order Mock Theta Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 284-290
-
- Article
-
- You have access
- Export citation
Beurling's Theorem and Characterization of Heat Kernel for Riemannian Symmetric Spaces of Noncompact Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 291-312
-
- Article
-
- You have access
- Export citation
On Cauchy–Liouville–Mirimanoff Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 313-320
-
- Article
-
- You have access
- Export citation