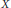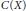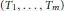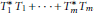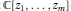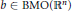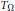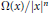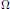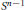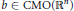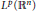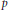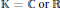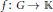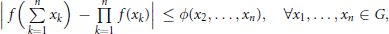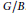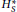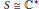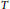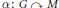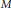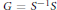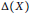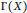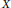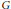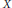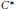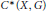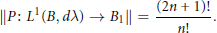Research Article
Approximate Amenability of Segal Algebras II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-6
-
- Article
-
- You have access
- Export citation
Characters on C(X)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 7-8
-
- Article
-
- You have access
- Export citation
Irreducible Tuples Without the Boundary Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 9-18
-
- Article
-
- You have access
- Export citation
Compact Commutators of Rough Singular Integral Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 19-29
-
- Article
-
- You have access
- Export citation
On an Exponential Functional Inequality and its Distributional Version
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 30-43
-
- Article
-
- You have access
- Export citation
Orbits of Geometric Descent
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 44-50
-
- Article
-
- You have access
- Export citation
Spectral Flows of Dilations of Fredholm Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 51-68
-
- Article
-
- You have access
- Export citation
Correction
Correction to “Infinite Dimensional DeWitt Supergroups and Their Bodies”
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 69-70
-
- Article
-
- You have access
- Export citation
Research Article
Limited Sets and Bibasic Sequences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 71-79
-
- Article
-
- You have access
- Export citation
The Equivariant Cohomology Rings of Peterson Varieties in All Lie Types
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 80-90
-
- Article
-
- You have access
- Export citation
Essential Commutants of Semicrossed Products
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 91-104
-
- Article
-
- You have access
- Export citation
On Graphs Associated with Character Degrees and Conjugacy Class Sizes of Direct Products of Finite Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 105-109
-
- Article
-
- You have access
- Export citation
Property T and Amenable Transformation Group C*-algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 110-114
-
- Article
-
- You have access
- Export citation
Weak Arithmetic Equivalence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 115-127
-
- Article
-
- You have access
- Export citation
A Sharp Constant for the Bergman Projection
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 128-133
-
- Article
-
- You have access
- Export citation
On the Generalized Auslander–Reiten Conjecture under Certain Ring Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 134-143
-
- Article
-
- You have access
- Export citation
Localization and Completeness in L2(ℝ)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 144-149
-
- Article
-
- You have access
- Export citation
Connections Between Metric Characterizations of Superreflexivity and the Radon–Nikodým Property for Dual Banach Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 150-157
-
- Article
-
- You have access
- Export citation
Correction
Corrigendum to “Chen Inequalities for Submanifolds of Real Space Forms with a Semi-symmetric Non-metric Connection”
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 158-159
-
- Article
-
- You have access
- Export citation
Research Article
Some Normal Numbers Generated by Arithmetic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 160-173
-
- Article
-
- You have access
- Export citation