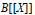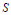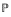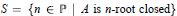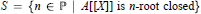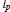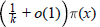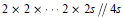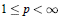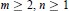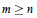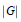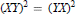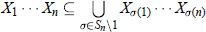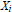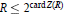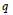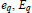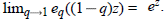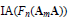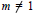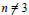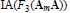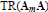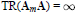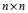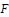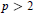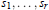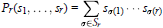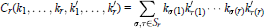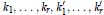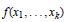Research Article
Root Closure in Integral Domains, III
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-9
-
- Article
-
- You have access
- Export citation
Simple Conditions for Matrices to be Bounded Operators on lp
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 10-14
-
- Article
-
- You have access
- Export citation
Sequences with Translates Containing Many Primes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 15-19
-
- Article
-
- You have access
- Export citation
A New Cohomological Criterion for the p-Nilpotence of Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 20-22
-
- Article
-
- You have access
- Export citation
Subordinacy Analysis and Absolutely Continuous Spectra for Sturm-Liouville Equations with Two Singular Endpoints
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 23-27
-
- Article
-
- You have access
- Export citation
Gorenstein Graded Algebras and the Evaluation Map
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 28-32
-
- Article
-
- You have access
- Export citation
Asymptotic Existence of Tight Orthogonal Main Effect Plans
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 33-40
-
- Article
-
- You have access
- Export citation
On the Clarke Subdifferential of an Integral Functional on Lp, 1 ≤ p < ∞
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 41-48
-
- Article
-
- You have access
- Export citation
Stability of Weighted Darma Filters
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 49-64
-
- Article
-
- You have access
- Export citation
Criteria for Commutativity in Large Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 65-70
-
- Article
-
- You have access
- Export citation
Splitting Patterns and Trace Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 71-78
-
- Article
-
- You have access
- Export citation
An Answer to a Question of Kegel on Sums of Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 79-80
-
- Article
-
- You have access
- Export citation
The Cardinality of the Center of a PI Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 81-85
-
- Article
-
- You have access
- Export citation
On q-Exponential Functions for |q| = 1
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 86-97
-
- Article
-
- You have access
- Export citation
Automorphisms of Metabelian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 98-104
-
- Article
-
- You have access
- Export citation
An Explicit Criterion for the Convexity of Quaternionic Numerical Range
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 105-108
-
- Article
-
- You have access
- Export citation
On Generalized Third Dimension Subgroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 109-117
-
- Article
-
- You have access
- Export citation
On Permanental Identities of Symmetric and Skew-Symmetric Matrices in Characteristic p
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 118-124
-
- Article
-
- You have access
- Export citation
Uniform Approximation to Mahler’s Measure in Several Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 125-128
-
- Article
-
- You have access
- Export citation