Article contents
An Answer to a Question of Kegel on Sums of Rings
Published online by Cambridge University Press: 20 November 2018
Abstract
We construct a ring 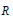 $R$ which is a sum of two subrings
$R$ which is a sum of two subrings 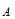 $A$ and
$A$ and 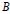 $B$ such that the Levitzki radical of
$B$ such that the Levitzki radical of 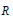 $R$ does not contain any of the hyperannihilators of
$R$ does not contain any of the hyperannihilators of 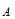 $A$ and
$A$ and 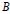 $B$. This answers an open question asked by Kegel in 1964.
$B$. This answers an open question asked by Kegel in 1964.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
- 4
- Cited by


