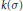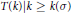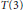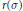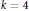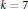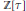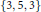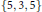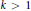Research Article
Dedication: Ted Bisztriczky
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 323-326
-
- Article
-
- You have access
- Export citation
Geometric “Floral” Configurations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 327-341
-
- Article
-
- You have access
- Export citation
On the X-ray Number of Almost Smooth Convex Bodies and of Convex Bodies of Constant Width
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 342-348
-
- Article
-
- You have access
- Export citation
On Projection Bodies of Order One
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 349-360
-
- Article
-
- You have access
- Export citation
A Note on Covering by Convex Bodies
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 361-365
-
- Article
-
- You have access
- Export citation
A Class of Cellulated Spheres with Non-Polytopal Symmetries
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 366-379
-
- Article
-
- You have access
- Export citation
Successive Minima and Radii
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 380-387
-
- Article
-
- You have access
- Export citation
Transversals with Residue in Moderately Overlapping T(k)-Families of Translates
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 388-402
-
- Article
-
- You have access
- Export citation
Shaken Rogers's Theorem for Homothetic Sections
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 403-406
-
- Article
-
- You have access
- Export citation
On the Bezdek–Pach Conjecture for Centrally Symmetric Convex Bodies
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 407-415
-
- Article
-
- You have access
- Export citation
Hamiltonian Properties of Generalized Halin Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 416-423
-
- Article
-
- You have access
- Export citation
Covering Discs in Minkowski Planes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 424-434
-
- Article
-
- You have access
- Export citation
Modular Reduction in Abstract Polytopes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 435-450
-
- Article
-
- You have access
- Export citation
Indecomposable Coverings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 451-463
-
- Article
-
- You have access
- Export citation
Two Volume Product Inequalities and Their Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 464-472
-
- Article
-
- You have access
- Export citation