Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-22T23:24:51.495Z Has data issue: false hasContentIssue false
  • English
  • Français

Indecomposable Coverings

Published online by Cambridge University Press:  20 November 2018

János Pach ,
Gábor Tardos  and
Géza Tóth
János Pach
Affiliation:
City College, CUNY and Courant Institute of Mathematical Sciences, New York University, New York, NY 10012, U.S.A. e-mail: pach@cims.nyu.edu
Gábor Tardos
Affiliation:
School of Computer Science, Simon Fraser University, Burnaby, BC, V5A 1S6 e-mail: tardos@cs.sfu.ca
Géza Tóth
Affiliation:
Rényi Institute, Hungarian Academy of Sciences, P.O.B. 127 Budapest, 1364, Hungary e-mail: geza@renyi.hu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

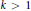We prove that for every $k\,>\,1$, there exist $k$-fold coverings of the plane (i) with strips, (ii) with axis-parallel rectangles, and (iii) with homothets of any fixed concave quadrilateral, that cannot be decomposed into two coverings. We also construct for every 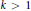$k\,>\,1$ a set of points 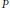$P$ and a family of disks 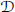$D$ in the plane, each containing at least $k$ elements of 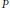$P$, such that, no matter how we color the points of 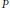$P$ with two colors, there exists a disk 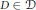$D\,\in \,D$ all of whose points are of the same color.

Keywords

52C1505C15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 3 , 01 September 2009 , pp. 451 - 463
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Alon, N. and Spencer, J. H., The Probabilistic Method. Second edition. Wiley, New York, 2000.Google Scholar
[2] Blundon, W. J., Multiple covering of the plane by circles. Mathematika 4(1957), 7–16.Google Scholar
[3] Bolle, U., On the density of multiple packings and coverings of convex discs. Studia Sci. Math. Hungar. 24(1989), 119–126.Google Scholar
[4] Brass, P., Pach, J., and Moser, W., Research Problems in Discrete Geometry. Springer, New York, 2005, p. 77.Google Scholar
[5] Chen, X., Pach, J., Szegedy, M., and Tardos, G., Delaunay graphs of point sets in the plane with respect to axis-parallel rectangles. Random Structures Algorithms 34(2008), 11–23.Google Scholar
[6] Cohn, M. J., Multiple lattice covering of space. Proc. London Math. Soc. 32(1976), 117–132.Google Scholar
[7] Dumir, V. C. and Hans-Gill, R. J., Lattice double packings in the plane. Indian J. Pure Appl. Math. 3(1972), 481–487.Google Scholar
[8] Erdʺos, P. and Rogers, C. A., Covering space with convex bodies. Acta Arith. 7(1961/1962), 281–285.Google Scholar
[9] Tóth, G. Fejes, A problem connected with multiple circle-packings and circle-coverings. Studia Sci. Math. Hungar. 12(1977), 447–456.Google Scholar
[10] Tóth, G. Fejes, New results in the theory of packing and covering. In: Convexity and Its Applications. Birkhäuser, Basel, 1983, pp. 318–359.Google Scholar
[11] Tóth, G. Fejes, Multiple lattice packings of symmetric convex domains in the plane. J. London Math. Soc. 29(1984), 556–561.Google Scholar
[12] Tóth, G. Fejes and Kuperberg, W., A survey of recent results in the theory of packing and covering. In: New Trends in Discrete and Computational Geometry, Algorithms Combin 10. Springer, Berlin, 1993, pp. 251–279.Google Scholar
[13] Few, L., The double packing of spheres. J. LondonMath. Soc. 28(1953), 297–304.Google Scholar
[14] Florian, A., Mehrfache Packung konvexer Körper. österreich. Akad.Wiss.Math.-Natur. Kl. Sitzungsber. II 186(1978), 373–384.Google Scholar
[15] Füredi, Z. and Kang, J.-H., Covering Euclidean n-space by translates of a convex body. Discrete Math 308(2008), 4495–4500.Google Scholar
[16] Hales, A. W. and Jewett, R. I., Regularity and positional games. Trans. Amer. Math. Soc. 106(1963), 222–229.Google Scholar
[17] Heppes, A., über mehrfache Kreislagerungen. Elem.Math. 10(1955), 125–127.Google Scholar
[18] Heppes, A., Mehrfache gitterförmige Kreislagerungen in der Ebene. Acta Math. Acad. Sci. Hungar. 10(1959), 141–148.Google Scholar
[19] Kostochka, A., Coloring intersection graphs of geometric figures with a given clique number. In: Towards a Theory of Geometric Graphs, Contemp. Math. 342, American Mathematical Society, Providence, RI, 2004, 127–138.Google Scholar
[20] Mani-Levitska, P. and Pach, J., Decomposition problems for multiple coverings with unit balls, manuscript, 1987. http://www.math.nyu.edu/_pach/publications/unsplittable.pdf. Google Scholar
[21] Pach, J., Decomposition of multiple packing and covering. 2. Kolloquium über Diskrete Geometrie, Salzburg, 1980, 169–178.Google Scholar
[22] Pach, J., Covering the Plane with Convex Polygon. Discrete Comput. Geom. 1(1986), 73–81.Google Scholar
[23] Pach, J. and Agarwal, P. K., Combinatorial Geometry. Wiley, New York, 1995.Google Scholar
[24] Schmidt, W. M., Zur Lagerung kongruenter Körper im Raum. Monatsh. Math. 65(1961), 154–158.Google Scholar
[25] Tardos, G. and Tóth, G., Multiple coverings of the plane with triangles. Discrete Comput. Geom. 38(2007), 443–450.Google Scholar