Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-05-15T02:33:01.284Z Has data issue: false hasContentIssue false
  • English
  • Français

A Class of Cellulated Spheres with Non-Polytopal Symmetries

Published online by Cambridge University Press:  20 November 2018

Gábor Gévay
Gábor Gévay*
Affiliation:
Bolyai Institute, University of Szeged, Aradi vértanúk tere 1, H-6720 Szeged, Hungary e-mail: gevay@math.u-szeged.hu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct, for all 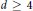$d\,\ge \,4$, a cellulation of 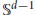${{\mathbb{S}}^{d-1}}$. We prove that these cellulations cannot be polytopal with maximal combinatorial symmetry. Such non-realizability phenomenon was first described in dimension 4 by Bokowski, Ewald and Kleinschmidt, and, to the knowledge of the author, until now there have not been any known examples in higher dimensions. As a starting point for the construction, we introduce a new class of (Wythoffian) uniform polytopes, which we call duplexes. In proving our main result, we use some tools that we developed earlier while studying perfect polytopes. In particular, we prove perfectness of the duplexes; furthermore, we prove and make use of the perfectness of another new class of polytopes which we obtain by a variant of the so-called $E$-construction introduced by Eppstein, Kuperberg and Ziegler.

Keywords

52B1152B1552B70CW spherepolytopalityautomorphism groupsymmetry groupuniform polytope
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 3 , 01 September 2009 , pp. 366 - 379
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Billera, L. J. and Björner, A., Face numbers of polytopes and complexes. In: Handbook of Discrete and Computational Geometry. CRC Press, Boca Raton, FL, 1997, pp. 291–315.Google Scholar
[2] Björner, A., Vergnas, M. Las, Sturmfels, B., White, N., and Ziegler, G. M., Oriented Matroids. Encyclopedia of Mathematics and its Applications, 46. Cambridge University Press, Cambridge, 1999.Google Scholar
[3] Bokowski, J., On the geometric flat embedding of abstract complexes with symmetries. In: Symmetry of Discrete Mathematical Structures and Their Symmetry Groups. A Collection of Essays. Research and Exposition inMathematics 15. Heldermann Verlag, Berlin, 1991, pp. 1–48.Google Scholar
[4] Bokowski, J., Computational Oriented Matroids. Cambridge University Press, Cambridge, 2006.Google Scholar
[5] Bokowski, J., Bremner, D. and Gévay, G., Symmetric matroid polytopes and their generation. To appear in European J. Combin.Google Scholar
[6] Bokowski, J., Cara, P. and Mock, S., On a self dual 3-sphere of Peter McMullen. Period. Math. Hungar. 39(1999), 17–32.Google Scholar
[7] Bokowski, J., Ewald, G. and Kleinschmidt, P., On combinatorial and affine automorphisms of polytopes. Israel J. Math. 47(1984) 123–130.Google Scholar
[8] Bokowski, J. and Sturmfels, B., Computational Synthetic Geometry. Lecture Notes inMathematics 1355, Springer-Verlag, Berlin, 1989.Google Scholar
[9] Coxeter, H. S. M., Wythoff 's construction for uniform polytopes. In: Twelve Geometric Essays. Southern Illinois University Press, Carbondale, 1968, pp. 40–53.Google Scholar
[10] Coxeter, H. S. M., Regular skew polyhedra in three and four dimensions, and their topological analogues, In: Twelve Geometric Essays. Southern Illinois University Press, Carbondale, 1968, pp. 75–105.Google Scholar
[11] Coxeter, H. S. M., Regular Polytopes, Methuen, London, 1948.Google Scholar
[12] Coxeter, H. S. M., Regular and semi-regular polytopes II, In: Kaleidoscopes. SelectedWritings of H. S. M. Coxeter. Wiley, New York, 1995.Google Scholar
[13] Eppstein, D., Kuperberg, G. and Ziegler, G. M., Fat 4-polytopes and fatter 3-spheres. In: Discrete Geometry. Pure Appl. Math. 253. Marcel Dekker, New York, 2003, pp. 239–265.Google Scholar
[14] Gabrielov, A. M., Gelfand, I. M. and Losik, M. V., Combinatorial computation of characteristic classes(in Russian), Funkcional. Anal. i Prilozhen. 9(1975), 12–28.Google Scholar
[15] Gévay, G., On perfect 4-polytopes. Beiträge Algebra Geom. 43(2002), 243–259.Google Scholar
[16] Gévay, G., Construction of non-Wythoffian perfect 4-polytopes. Beiträge Algebra Geom. 44(2003), 235–244.Google Scholar
[17] Gévay, G. and Miyazaki, K., Some examples of semi-nodal perfect 4-polytopes. Publ. Math. Debrecen 63(2003), 715–735.Google Scholar
[18] Grünbaum, B., Convex Polytopes, Graduate Texts in Mathematics 221. Springer-Verlag, New York, 2003.Google Scholar
[19] Grünbaum, B. and Shephard, G. C., Convex polytopes. Bull. LondonMath. Soc. 1(1969), 257–300.Google Scholar
[20] Hartley, M. I., Simpler tests for semisparse subgroups. Ann. Comb. 10(2006), 343–352.Google Scholar
[21] Kalai, G., Polytope skeletons and paths. In: Handbook of Discrete and Computational Geometry. CRC Press, Boca Raton, FL, 1997, pp. 331–354.Google Scholar
[22] Madden, T. M., A classification of perfect solids. Beiträge Algebra Geom. 36(1995), 261–279.Google Scholar
[23] Mani, P., Automorphismen von polyedrischen Graphen. Math. Ann. 192(1971), 279–303.Google Scholar
[24] Mihalisin, J. and Williams, G., Nonconvex embeddings of the exceptional simplicial 3-spheres with 8 vertices. J. Comb. Theory Ser. A, 98(2002), 74–86.Google Scholar
[25] Paffenholz, A., Constructions for posets, lattices, and polytopes. Ph.D. Thesis, Technical University of Berlin, 2005. http://edocs.tu-berlin.de/diss/2005/paffenholz andreas.pdf.Google Scholar
[26] Paffenholz, A., New polytopes from products. J. Combin. Theory Ser. A 113(2006), 1396–1418.Google Scholar
[27] Paffenholz, A. and Ziegler, G. M., The Et -construction for lattices, spheres and polytopes. Discrete Comp. Geom. 32(2004), 601–621.Google Scholar
[28] Pfeifle, J. and Ziegler, G. M., Many triangulated 3-spheres. Math. Ann. 330(2004), 829–837.Google Scholar
[29] Richter-Gebert, J., The universality theorems for oriented matroids and polytopes. In: Advances in Discrete and Computational Geometry. Contemporary Mathematics 223, American Mathematical Society, Providence, RI, 1999, pp. 269–292.Google Scholar
[30] Robertson, S. A., Polytopes and Symmetry. London Math. Soc. Lecture Notes Series 90, Cambridge University Press, Cambridge, 1984.Google Scholar
[31] Schulte, E., Symmetry of polytopes and polyhedra. In: Handbook of Discrete and Computational Geometry, CRC Press, Boca Raton, FL, 1997, pp. 311–330.Google Scholar
[32] Ziegler, G. M., Lectures on Polytopes. Graduate Texts in Mathematics 152, Springer-Verlag, New York, 1995.Google Scholar