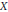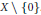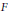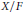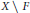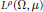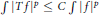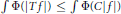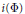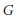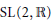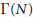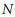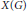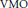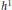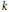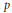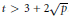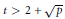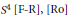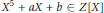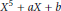Research Article
Real-Analytic Negligibility of Points and Subspaces in Banach Spaces, with Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-10
-
- Article
-
- You have access
- Export citation
Polycharacters of Cocommutative Hopf Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 11-24
-
- Article
-
- You have access
- Export citation
Extrapolation of Lp Data from a Modular Inequality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 25-35
-
- Article
-
- You have access
- Export citation
Modular Equations and Discrete, Genus-Zero Subgroups of SL(2, ℝ) Containing Γ(N)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 36-45
-
- Article
-
- You have access
- Export citation
Local VMO and Weak Convergence in h1
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 46-59
-
- Article
-
- You have access
- Export citation
Uniform Embeddings into Hilbert Space and a Question of Gromov
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 60-70
-
- Article
-
- You have access
- Export citation
Images of Additive Polynomials in 𝔽q((t)) Have the Optimal Approximation Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 71-79
-
- Article
-
- You have access
- Export citation
Approximation On Arcs and Dendrites Going to Infinity in ℂn
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 80-85
-
- Article
-
- You have access
- Export citation
On Cyclic Fields of Odd Prime Degree p with Infinite Hilbert p-Class Field Towers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 86-88
-
- Article
-
- You have access
- Export citation
On Gunning’s Prime Form in Genus 2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 89-96
-
- Article
-
- You have access
- Export citation
Invariant Measures and Natural Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 97-108
-
- Article
-
- You have access
- Export citation
The Distribution of Totatives
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 109-114
-
- Article
-
- You have access
- Export citation
The Number of Non-Zero Digits of n!
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 115-118
-
- Article
-
- You have access
- Export citation
The Grade Conjecture and the S2 Condition
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 119-122
-
- Article
-
- You have access
- Export citation
Uniform Distribution in Model Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 123-130
-
- Article
-
- You have access
- Export citation
The Topological Interpretation of the Core Group of a Surface in S4
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 131-137
-
- Article
-
- You have access
- Export citation
The Discriminant of a Dihedral Quintic Field Defined by a Trinomial X5 + aX + b
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 138-153
-
- Article
-
- You have access
- Export citation
On the Poisson Integral of Step Functions and Minimal Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 154-160
-
- Article
-
- You have access
- Export citation