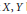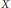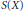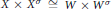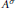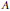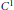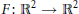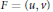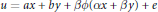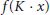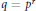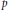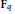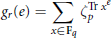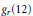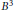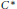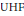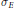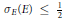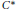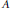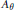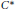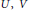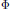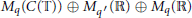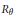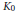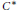Research Article
Discreteness For the Set of Complex Structures On a Real Variety
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 321-322
-
- Article
-
- You have access
- Export citation
Characterizing Two-Dimensional Maps Whose Jacobians Have Constant Eigenvalues
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 323-331
-
- Article
-
- You have access
- Export citation
Some Questions about Semisimple Lie Groups Originating in Matrix Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 332-343
-
- Article
-
- You have access
- Export citation
Gauss and Eisenstein Sums of Order Twelve
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 344-355
-
- Article
-
- You have access
- Export citation
Branched Covers of Tangles in Three-balls
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 356-364
-
- Article
-
- You have access
- Export citation
Homogeneity of the Pure State Space of a Separable
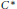 ${{C}^{*}}$-Algebra
${{C}^{*}}$-Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 365-372
-
- Article
-
- You have access
- Export citation
Potential Theory of the Farthest-Point Distance Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 373-387
-
- Article
-
- You have access
- Export citation
Tracially Quasidiagonal Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 388-399
-
- Article
-
- You have access
- Export citation
Approximating Positive Polynomials Using Sums of Squares
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 400-418
-
- Article
-
- You have access
- Export citation
On Non-Strongly Free Automorphisms of Subfactors of Type
 $\text{II}{{\text{I}}_{0}}$
$\text{II}{{\text{I}}_{0}}$
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 419-428
-
- Article
-
- You have access
- Export citation
The Grothendieck Trace and the de Rham Integral
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 429-440
-
- Article
-
- You have access
- Export citation
An Inductive Limit Model for the
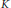 $K$-Theory of the Generator-Interchanging Antiautomorphism of an Irrational Rotation Algebra
$K$-Theory of the Generator-Interchanging Antiautomorphism of an Irrational Rotation Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 441-456
-
- Article
-
- You have access
- Export citation
Strongly Perforated
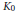 ${{K}_{0}}$-Groups of Simple
${{K}_{0}}$-Groups of Simple 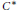 ${{C}^{*}}$-Algebras
${{C}^{*}}$-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 457-472
-
- Article
-
- You have access
- Export citation
A Multiplicative Analogue of Schur's Tauberian Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 473-480
-
- Article
-
- You have access
- Export citation