Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-24T13:09:34.581Z Has data issue: false hasContentIssue false
  • English
  • Français

Potential Theory of the Farthest-Point Distance Function

Published online by Cambridge University Press:  20 November 2018

Richard S. Laugesen  and
Igor E. Pritsker
Richard S. Laugesen
Affiliation:
Department of Mathematics University of Illinois Urbana, IL 61801 USA, email: laugesen@math.uiuc.edu
Igor E. Pritsker
Affiliation:
Department of Mathematics Oklahoma State University Stillwater, OK 74078 USA, email: igor@math.okstate.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the farthest-point distance function, which measures the distance from 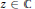$z\,\in \,\mathbb{C}$ to the farthest point or points of a given compact set $E$ in the plane.

The logarithm of this distance is subharmonic as a function of 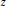$z$, and equals the logarithmic potential of a unique probability measure with unbounded support. This measure 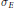${{\sigma }_{E}}$ has many interesting properties that reflect the topology and geometry of the compact set $E$. We prove 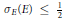${{\sigma }_{E}}(E)\,\le \,\frac{1}{2}$ for polygons inscribed in a circle, with equality if and only if $E$ is a regular $n$-gon for some odd $n$. Also we show 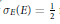${{\sigma }_{E}}(E)\,=\,\frac{1}{2}$ for smooth convex sets of constant width. We conjecture 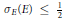${{\sigma }_{E}}(E)\,\le \,\frac{1}{2}$ for all $E$.

Keywords

31A0552A1052A40distance functionfarthest pointssubharmonic functionrepresenting measureconvex bodies of constant width
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 3 , 01 September 2003 , pp. 373 - 387
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Boyd, D. W., Sharp inequalities for the product of polynomials. Bull. London Math. Soc. 26 (1994), 449–454.Google Scholar
[2] Chakerian, G. D. and Groemer, H., Convex bodies of constant width. In: .Convexity and its Applications. (eds. P. M. Gruber and J. M.Wills), Birkhäuser, Basel, 1983, 49–96.Google Scholar
[3] Doob, J. L., Classical Potential Theory and Its Probabilistic Counterpart. Springer-Verlag, New York, 1984.Google Scholar
[4] Krantz, S. G. and Parks, H. R., Distance to Ck hypersurfaces. J. Differential Equations 40 (1981), 116–120.Google Scholar
[5] Krantz, S. G. and Parks, H. R., The Geometry of Domains in Space. Birkhäuser, Boston, 1999.Google Scholar
[6] Pritsker, I. E., Products of polynomials in uniform norms. Trans. Amer. Math. Soc. 353 (2001), 3971–3993.Google Scholar
[7] Ransford, T., Potential Theory in the Complex Plane. Cambridge Univ. Press, Cambridge, 1995.Google Scholar
[8] Rudin, W., Real and Complex Analysis. 3rd edition, McGraw-Hill, New York, 1987.Google Scholar
[9] Saff, E. B. and Totik, V., Logarithmic Potentials with External Fields. Springer-Verlag, Heidelberg, 1997.Google Scholar
[10] Webster, R., Convexity. Oxford University Press, Oxford, 1994.Google Scholar