Research Article
Efficient Presentations of the Groups PSL(2, 2p) and SL(2, 2p)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-10
-
- Article
-
- You have access
- Export citation
On the Residual Finiteness of Certain Polygonal Products
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 11-17
-
- Article
-
- You have access
- Export citation
A Note on Blaschke Products with Zeroes in a Nontangential Region
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 18-23
-
- Article
-
- You have access
- Export citation
A Note on the Dubois-Efroymson Dimension Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 24-29
-
- Article
-
- You have access
- Export citation
Tree self-embeddings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 30-33
-
- Article
-
- You have access
- Export citation
Asymptotic Properties of Semilinear Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 34-46
-
- Article
-
- You have access
- Export citation
Norm Inequalities for Generators of Analytic Semigroups and Cosine Operator Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 47-53
-
- Article
-
- You have access
- Export citation
Bireflectionality in Absolute Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 54-63
-
- Article
-
- You have access
- Export citation
On the Deterministic and Asymptotic σ-Algebras of a Markov Operator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 64-73
-
- Article
-
- You have access
- Export citation
A Note on the Rn,k Property for L1 (μ E)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 74-77
-
- Article
-
- You have access
- Export citation
Cauchy Completion Categories
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 78-84
-
- Article
-
- You have access
- Export citation
Isomorphic Group Rings Over Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 85-89
-
- Article
-
- You have access
- Export citation
Fixed Point Theorems for Lipspchitzian Semigroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 90-97
-
- Article
-
- You have access
- Export citation
Uniqueness of Preduals for Spaces of Continuous Vector Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 98-104
-
- Article
-
- You have access
- Export citation
On the Distribution of the Sequence {nd*(n)}
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 105-108
-
- Article
-
- You have access
- Export citation
Non-Standard, Normal Subgroups and Non-Normal, Standard Subgroups of the Modular Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 109-113
-
- Article
-
- You have access
- Export citation
On PIC(D[α]) For a Principal Ideal Domain D
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 114-116
-
- Article
-
- You have access
- Export citation
A Stochastic Ergodic Theorem for General Additive Processes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 117-121
-
- Article
-
- You have access
- Export citation
A New Space With no Locally Uniformly Rotund Renorming
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 122-128
-
- Article
-
- You have access
- Export citation

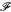
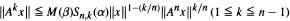


 measurable iff
measurable iff 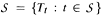 a continuous representation of
a continuous representation of 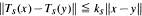 for
for 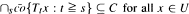 then
then 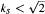 has a common fixed point in a Hilbert space. Next, we prove that the theorem is valid in a Banach space
has a common fixed point in a Hilbert space. Next, we prove that the theorem is valid in a Banach space 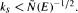
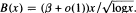 . In this note we give an explicit expression for
. In this note we give an explicit expression for 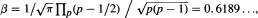 where the product is over all primes
where the product is over all primes 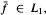 , such that
, such that 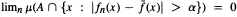 whenever α > 0 and
whenever α > 0 and 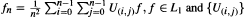 and {
and {