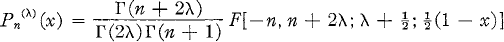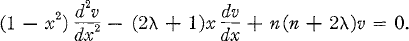Research Article
On Almost Regular Homeomorphisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-6
-
- Article
-
- You have access
- Export citation
On Integral Functions Having Prescribed Asymptotic Growth. II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 7-20
-
- Article
-
- You have access
- Export citation
Commutativity for Matrices of Quaternions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 21-24
-
- Article
-
- You have access
- Export citation
Bisimple Inverse Semigroups as Semigroups of Ordered Triples
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 25-39
-
- Article
-
- You have access
- Export citation
Enumeration of Graphs with given Partition
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 40-47
-
- Article
-
- You have access
- Export citation
Four-Dimension Equivalences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 48-50
-
- Article
-
- You have access
- Export citation
On the Properties of an Entire Function of Two Complex Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 51-57
-
- Article
-
- You have access
- Export citation
Free Vector Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 58-66
-
- Article
-
- You have access
- Export citation
Ramanujan Congruences for p-k(n)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 67-78
-
- Article
-
- You have access
- Export citation
A Riemann-Type Integral of Lebesgue Power
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 79-87
-
- Article
-
- You have access
- Export citation
Generalized Radical Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 88-94
-
- Article
-
- You have access
- Export citation
On Independent Complete Subgraphs in a Graph
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 95-102
-
- Article
-
- You have access
- Export citation
On the Gotlieb-Csima Time-Tabling Algorithm
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 103-119
-
- Article
-
- You have access
- Export citation
Generating Functions for Ultraspherical Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 120-134
-
- Article
-
- You have access
- Export citation
On Asymmetrical Derivates of Non-Differentiable Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 135-143
-
- Article
-
- You have access
- Export citation
Convex Sets of Non-Negative Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 144-157
-
- Article
-
- You have access
- Export citation
Axioms for Absolute Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 158-181
-
- Article
-
- You have access
- Export citation
Anneau De Fractions D'un J-Anneau
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 182-202
-
- Article
-
- You have access
- Export citation
Commutators of Matrices with Prescribed Determinant
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 203-221
-
- Article
-
- You have access
- Export citation
On Invariant Means which are Not Inverse Invariant
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 222-224
-
- Article
-
- You have access
- Export citation

 we shall denote by
we shall denote by 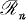 the ring of all
the ring of all 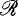 and by
and by 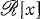 the set of all polynomials in
the set of all polynomials in 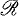 .
.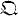 will denote the non-commutative four-dimensional division algebra of real quaternions with 1,
will denote the non-commutative four-dimensional division algebra of real quaternions with 1, 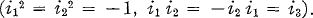
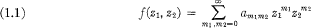
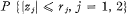 . Let
. Let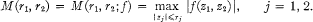
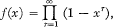
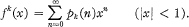
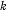 ; unfortunately his results are incorrect, because of an error in his Lemma 4 on which his main theorems depend. This error is essentially a misquotation of the results of Watson (5), which one may readily understand in view of Watson's formidable notation.
; unfortunately his results are incorrect, because of an error in his Lemma 4 on which his main theorems depend. This error is essentially a misquotation of the results of Watson (5), which one may readily understand in view of Watson's formidable notation.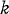 modes is called a
modes is called a 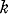 -graph
-graph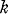 -graphs contained in a given graph
-graphs contained in a given graph