Article contents
Generating Functions for Ultraspherical Functions
Published online by Cambridge University Press: 20 November 2018
Extract
The ultraspherical function
1.1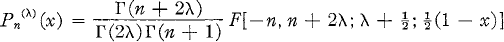
for |1 — x| < 2 is a solution of the differential equation
1.2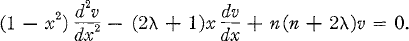
This equation has two independent solutions; of the two, only Pn(λ)(x) is analytic at x = 1, aside for some special values of λ, which we shall not consider.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1968
Footnotes
This paper is a condensation of a doctoral dissertation submitted at the University of New Brunswick in May 1965.
References
- 4
- Cited by


