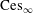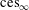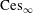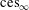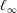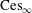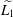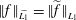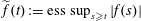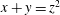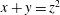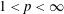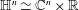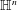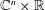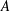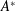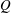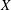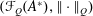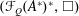Article
Isomorphic Structure of Cesàro and Tandori Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 501-532
-
- Article
-
- You have access
- Export citation
Lipschitz 1-connectedness for Some Solvable Lie Groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 533-555
-
- Article
-
- You have access
- Export citation
Degrees of Regular Sequences With a Symmetric Group Action
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 557-578
-
- Article
-
- You have access
- Export citation
Monochromatic Solutions to
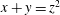 $x+y=z^{2}$
$x+y=z^{2}$
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 579-605
-
- Article
-
- You have access
- Export citation
Marcinkiewicz Multipliers and Lipschitz Spaces on Heisenberg Groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 607-627
-
- Article
-
- You have access
- Export citation
Smoothing of Limit Linear Series on Curves and Metrized Complexes of Pseudocompact Type
- Part of:
-
- Published online by Cambridge University Press:
- 16 October 2018, pp. 629-658
-
- Article
-
- You have access
- Export citation
Freeness and The Partial Transposes of Wishart Random Matrices
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 659-681
-
- Article
-
- You have access
- Export citation
The Mod Two Cohomology of the Moduli Space of Rank Two Stable Bundles on a Surface and Skew Schur Polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 683-715
-
- Article
-
- You have access
- Export citation
Fourier Spaces and Completely Isometric Representations of Arens Product Algebras
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 717-747
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
CJM volume 71 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
CJM volume 71 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation