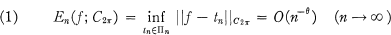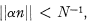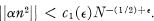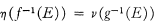Research Article
Finite Groups Admitting an Automorphism Trivial on a Sylow 2-Subgroup
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 889-896
-
- Article
-
- You have access
- Export citation
A Characterization of Starshaped Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-680
-
- Article
-
- You have access
- Export citation
Green's Potentials with Prescribed Boundary Values
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 681-686
-
- Article
-
- You have access
- Export citation
Weak q-Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 687-695
-
- Article
-
- You have access
- Export citation
Systems that are Purely Simple and Pure Injegtive
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 696-700
-
- Article
-
- You have access
- Export citation
Complex Approximation and Simultaneous Interpolation on Closed Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 701-706
-
- Article
-
- You have access
- Export citation
A Topological Characterization of Conjugate Nets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 707-721
-
- Article
-
- You have access
- Export citation
CPI-Extensions: Overrings of Integral Domains with Special Prime Spectrums
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 722-737
-
- Article
-
- You have access
- Export citation
A Canonical Factorization for Graph Homomorphisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 738-743
-
- Article
-
- You have access
- Export citation
Changes of Variables Preserving Fourier-Stieltjes Transforms on Simply Connected Nilpotent Lie Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 744-755
-
- Article
-
- You have access
- Export citation
Cyclic Transformations of Polygons and the Generalized Inverse
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 756-770
-
- Article
-
- You have access
- Export citation
The Caratheodory Metric and its Majorant Metrics
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 771-780
-
- Article
-
- You have access
- Export citation
Best Trigonometric Approximation, Fractional Order Derivatives and Lipschitz Classes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 781-793
-
- Article
-
- You have access
- Export citation
Rice Theorems for ∑n-1 Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 794-805
-
- Article
-
- You have access
- Export citation
On Upcrossing Probabilities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 806-818
-
- Article
-
- You have access
- Export citation
On the Distribution Modulo 1 of the Sequence αn2 + βn
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 819-826
-
- Article
-
- You have access
- Export citation
Certain Integral Equalities which Imply Equimeasurability of Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 827-844
-
- Article
-
- You have access
- Export citation
On Rank 3 Groups Having λ = 0
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 845-847
-
- Article
-
- You have access
- Export citation
A Sufficient Condition for Solvability in Groups Admitting Elementary Abelian Operator Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 848-855
-
- Article
-
- You have access
- Export citation
On Some Classes of Primary Banach Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 856-873
-
- Article
-
- You have access
- Export citation



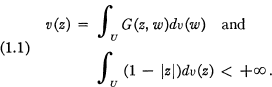
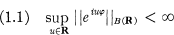
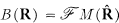 denotes the space of Fourier-Stieltjes transforms on R.)
denotes the space of Fourier-Stieltjes transforms on R.) be a fixed point in
be a fixed point in 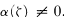 .
.