Research Article
Finite p-groups with Isomorphic Subgroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-13
-
- Article
-
- You have access
- Export citation
Ergodic Theory and Averaging Iterations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 14-23
-
- Article
-
- You have access
- Export citation
Axioms for an n-metric Structure
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 24-30
-
- Article
-
- You have access
- Export citation
ULC Properties in Neighbourhoods of Embedded Surfaces and Curves in E3
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 31-73
-
- Article
-
- You have access
- Export citation
A Theorem for Enumerating Certain Types of Collections
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 74-82
-
- Article
-
- You have access
- Export citation
The Existence of Quadratic Differentials in Simply Connected Regions of the Complex Plane
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 83-91
-
- Article
-
- You have access
- Export citation
Isometries of Hp(Un)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 92-95
-
- Article
-
- You have access
- Export citation
The Classification of Factors is not Smooth
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 96-102
-
- Article
-
- You have access
- Export citation
The Strong Perfect Graph Conjecture for Planar Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 103-114
-
- Article
-
- You have access
- Export citation
A Note on Generalized Direct Products of Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 115-116
-
- Article
-
- You have access
- Export citation
Plücker Coordinates for Regular Chain Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 117-126
-
- Article
-
- You have access
- Export citation
On the Peano Derivatives
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 127-140
-
- Article
-
- You have access
- Export citation
The Algebra of Differentials of Infinite Rank
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 141-155
-
- Article
-
- You have access
- Export citation
Uniqueness Theorems for a Singular Partial Differential Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 156-163
-
- Article
-
- You have access
- Export citation
L'enveloppe de Translations d'un Demi-Treillis de Groupes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 164-177
-
- Article
-
- You have access
- Export citation
Generalized Spectral Theory and Second Order Ordinary Differential Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 178-193
-
- Article
-
- You have access
- Export citation
Integral Limit Laws for Additive Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 194-203
-
- Article
-
- You have access
- Export citation
From Path Lifting and Unique Arc Lifting to Unique Path Lifting
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 204-212
-
- Article
-
- You have access
- Export citation
Non-Existence Criteria for Small Configurations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 213-215
-
- Article
-
- You have access
- Export citation
On the Uniform Approximation of Smooth Functions by Jacobi Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 216-223
-
- Article
-
- You have access
- Export citation

 denote the algebraic isomorphism classes in
denote the algebraic isomorphism classes in 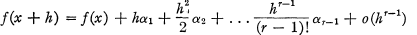
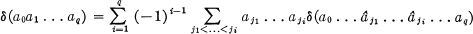
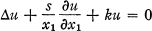
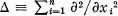 is the Laplacian operator on
is the Laplacian operator on 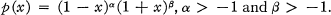
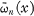 we Have
we Have