Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T14:16:56.210Z Has data issue: false hasContentIssue false
  • English
  • Français

The Classification of Factors is not Smooth

Published online by Cambridge University Press:  20 November 2018

E. J. Woods
E. J. Woods*
Affiliation:
Queen's University, Kingston, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There is a natural Borel structure on the set F of all factors on a separable Hilbert space [3]. Let 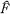denote the algebraic isomorphism classes in F together with the quotient Borel structure. Now that various non-denumerable families of mutually non-isomorphic factors are known to exist [1; 6; 8; 10; 11; 12; 13], the most obvious question to be resolved is whether or not 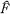is smooth (i.e. is there a countable family of Borel sets which separate points). We answer this question negatively by an explicit construction.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 25 , Issue 1 , February 1973 , pp. 96 - 102
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. Araki, H. and Woods, E. J., A classification of factors, Publ. Res. Inst. Math. Sci. Ser. A 4 (1968), 51–130.Google Scholar
2. Effros, E., Transformation groups and C*-algebras, Ann. of Math. 81 (1965), 38–55.Google Scholar
3. Effros, E., The Borel space of von Neumann algebras on a separable Hilbert space, Pacific J. Math. 15 (1965), 1153-1164. 4^ Global structure in von Neumann algebras, Trans. Amer. Math. Soc. 121 (1966), 434–454.Google Scholar
5. Glimm, J., Type I C*-algebras, Ann. of Math. 73 (1961), 572–612.Google Scholar
6. Krieger, W., On a class of hyperfinite factors that arise from null-recurrent Markov chains, J. Functional Analysis 7 (1971), 27–42.Google Scholar
7. Mackey, G. W., Borel structure in groups and their duals, Trans. Amer. Math. Soc. 85 (1957), 134–165.Google Scholar
8. McDuff, D., Uncountably many Ui-factors, Ann. of Math. 90 (1969), 372–377.Google Scholar
9. Nielsen, O. A., An example of a von Neumann algebra of global type II (to appear).Google Scholar
10. Powers, R. T., Representations of uniformly hyperfinite algebras and their associated von Neumann rings, Ann. of Math. 86 (1967), 138–171.Google Scholar
11. Sakai, S., An uncountable number of II1 and II∞-factors, J. Functional Analysis 5 (1970), 236–246.Google Scholar
12. Sakai, S., An uncountable family of non-hyperfinite type Ill-factors, Functional analysis (edited by Wilde, C. O., Academic Press, New York, 1970).Google Scholar
13. Williams, J., Non-isomorphic tensor products of von Neumann algebras (to appear).Google Scholar