Article contents
On the Peano Derivatives
Published online by Cambridge University Press: 20 November 2018
Extract
Let f be a real valued function defined in some neighbourhood of a point x. If there are numbers α1, α2, … αr-1, independent of h such that
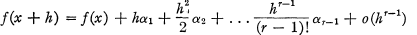
then the number αk is called the kth Peano derivative (also called kth de la Vallée Poussin derivative [6]) of f at x and we write αk = fk(x). It is convenient to write α0 = f0(x) = f(x). The definition is such that if the mth Peano derivative exists so does the nth for 0 ≦ n ≦ m.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1973
References
- 4
- Cited by




