Research Article
On the Embedding into a Ring of an Archimedean ι-Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-8
-
- Article
-
- You have access
- Export citation
Some Extreme Rays of the Positive Pluriharmonic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 9-16
-
- Article
-
- You have access
- Export citation
Planar Sublattices of a Free Lattice. II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 17-34
-
- Article
-
- You have access
- Export citation
A Theory of Uniformities for Generalized Ordered Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 35-44
-
- Article
-
- You have access
- Export citation
The Asymptotic Behaviour of Equidistant Permutation Arrays
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 45-48
-
- Article
-
- You have access
- Export citation
Polynomial Approximation and Growth of Generalized Axisymmetrig Potentials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 49-59
-
- Article
-
- You have access
- Export citation
Labeled Bipartite Blocks
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 60-68
-
- Article
-
- You have access
- Export citation
Characterizations of Finite Lattices that are Bounded-Homomqrphic Images or Sublattices of Free Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 69-78
-
- Article
-
- You have access
- Export citation
The Maximal Ideal Space of H∞ + C on the ball in Cn
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 79-86
-
- Article
-
- You have access
- Export citation
Comments On a Discreteness Condition for Subgroups of SL(2, C)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 87-92
-
- Article
-
- You have access
- Export citation
Rings Characterized by their Cyclic Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 93-111
-
- Article
-
- You have access
- Export citation
Coinitial Grapfis and Whitehead Automorphisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 112-123
-
- Article
-
- You have access
- Export citation
Quelques Propriétés Sur Le Normalisateur D'un Pseudogroupe De Lie Transitif
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 124-129
-
- Article
-
- You have access
- Export citation
Embedding Smooth Dendroids in Hyperspaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 130-138
-
- Article
-
- You have access
- Export citation
Invariant Complements to Closed Invariant Subspaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 139-147
-
- Article
-
- You have access
- Export citation
Lifting the Commutant of a Subnormal Operator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 148-156
-
- Article
-
- You have access
- Export citation
The Structure of Semisimple Symmetric Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 157-180
-
- Article
-
- You have access
- Export citation
On a Class of Analytic Functions of Smirnov
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 181-183
-
- Article
-
- You have access
- Export citation
An Inductive Rearrangement Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 184-188
-
- Article
-
- You have access
- Export citation
Some Radical Properties of Jordan Matrix Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 189-196
-
- Article
-
- You have access
- Export citation

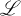 be the category which has objects archimedean
be the category which has objects archimedean 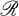 be the category with objects archimedean
be the category with objects archimedean 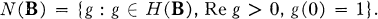
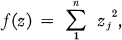
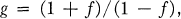
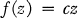
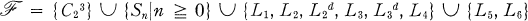
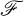 as a sublattice.
as a sublattice.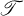 )
)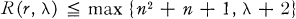
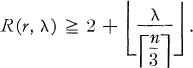
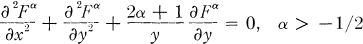
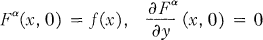
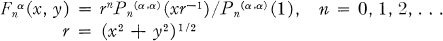
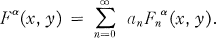
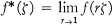
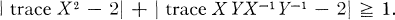
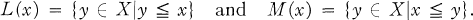
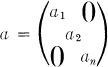
 where the
where the