Research Article
Central Quotients and Coverings of Steinberg Unitary Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-482
-
- Article
-
- You have access
- Export citation
The Exponent of the Homotopy Groups of Moore Spectra and the Stable Hurewicz Homomorphism
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 483-495
-
- Article
-
- You have access
- Export citation
Bounded Pointwise Approximation of Solutions of Elliptic Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 496-511
-
- Article
-
- You have access
- Export citation
The Addition of Primes and Power
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 512-526
-
- Article
-
- You have access
- Export citation
On Weighted Sobolev Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 527-541
-
- Article
-
- You have access
- Export citation
A Schilder Type Theorem for Super-Brownian Motion
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 542-568
-
- Article
-
- You have access
- Export citation
Maps in Locally Orientable Surfaces, the Double Coset Algebra, and Zonal Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 569-584
-
- Article
-
- You have access
- Export citation
Generators of Ideals Defining Certain Surfaces in Projective Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 585-595
-
- Article
-
- You have access
- Export citation
Rings With Finite Maximal Invariant Subrings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 596-606
-
- Article
-
- You have access
- Export citation
Structural Properties of Weak Cotype 2 Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 607-624
-
- Article
-
- You have access
- Export citation
Complemented Copies of ℓ1 and Pełczyński's Property (V*) in Bochner Function Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 625-640
-
- Article
-
- You have access
- Export citation
Diffusion on Lie Groups (III)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 641-672
-
- Article
-
- You have access
- Export citation



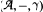 , where
, where 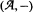 is a unital nonassociative algebra with involution and
is a unital nonassociative algebra with involution and 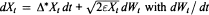 a space-time white noise. A Schilder type theorem is established concerning large deviation probabilities of
a space-time white noise. A Schilder type theorem is established concerning large deviation probabilities of 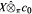 or it is equivalent to the unit vector basis of
or it is equivalent to the unit vector basis of