Research Article
Average normalisations of elliptic curves
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-358
-
- Article
-
- You have access
- Export citation
Some properties of Fatou and Julia sets of transcendental meromorphic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-8
-
- Article
-
- You have access
- Export citation
Convolution of Riemannian manifolds and its applications
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-191
-
- Article
-
- You have access
- Export citation
Construction of sunny nonexpansive retractions in Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 9-16
-
- Article
-
- You have access
- Export citation
Smoothing spline in a convex closed set of Hilbert space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 359-368
-
- Article
-
- You have access
- Export citation
Rigid sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 193-205
-
- Article
-
- You have access
- Export citation
Two hyperbolic Schwarz lemmas
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 17-24
-
- Article
-
- You have access
- Export citation
Topological sequence entropy and topologically weak mixing
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 207-211
-
- Article
-
- You have access
- Export citation
1-perfect codes in Sierpiński graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 369-384
-
- Article
-
- You have access
- Export citation
A note on tensor products of reflexive algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 25-31
-
- Article
-
- You have access
- Export citation
Steady vortex flows obtained from an inverse problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 213-226
-
- Article
-
- You have access
- Export citation
On boundedness of the weighted Bergman projections on the Lipschitz spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 385-391
-
- Article
-
- You have access
- Export citation
Characterisations of derivations on some operator algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 227-232
-
- Article
-
- You have access
- Export citation
A remark on Littlewood–Paley g-function
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 33-41
-
- Article
-
- You have access
- Export citation
Chapman-Jouguet detonation profile for a qualitative model
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 393-403
-
- Article
-
- You have access
- Export citation
Hitting probabilities of conditional Brownian motion and polarisation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 233-244
-
- Article
-
- You have access
- Export citation
Asymptotical smoothness and its applications
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 405-418
-
- Article
-
- You have access
- Export citation
A new minimax theorem and a perturbed James's theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 43-56
-
- Article
-
- You have access
- Export citation
On Helly's principle for metric semigroup valued BV mappings to two real variables
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 245-257
-
- Article
-
- You have access
- Export citation
Most finitely generated subgroups of infinite unitriangular matrices are free
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 419-423
-
- Article
-
- You have access
- Export citation



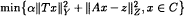 ,
, 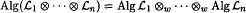 if Alg(ℒ
if Alg(ℒ