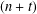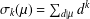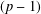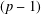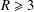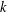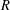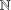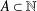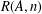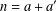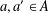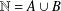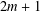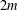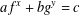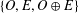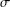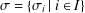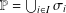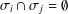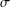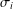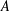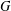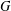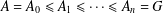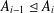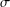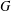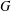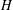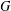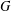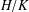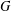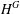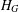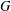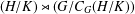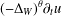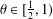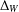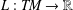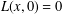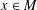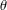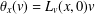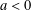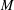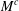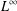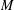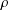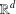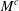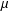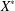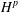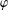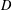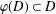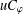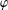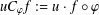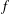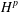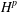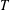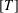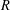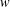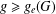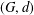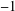Research Article
AN ANALOGUE OF EULER’S IDENTITY AND SPLIT PERFECT PARTITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2018, pp. 353-361
-
- Article
- Export citation
CONGRUENCES FOR THE
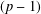 $(p-1)$TH APÉRY NUMBER
$(p-1)$TH APÉRY NUMBER
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2018, pp. 362-368
-
- Article
- Export citation
A NEW MENON’S IDENTITY FROM GROUP ACTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2018, pp. 369-375
-
- Article
- Export citation
FACTORS OF CARMICHAEL NUMBERS AND AN EVEN WEAKER
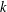 $k$-TUPLES CONJECTURE
$k$-TUPLES CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2019, pp. 376-384
-
- Article
- Export citation
ON PARTITIONS OF NONNEGATIVE INTEGERS AND REPRESENTATION FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2018, pp. 385-387
-
- Article
- Export citation
ON FINDING SOLUTIONS TO EXPONENTIAL CONGRUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 388-391
-
- Article
- Export citation
ON THE TRANSCENDENCE OF CERTAIN REAL NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2019, pp. 392-402
-
- Article
- Export citation
FINITE UNITARY RINGS IN WHICH ALL SYLOW SUBGROUPS OF THE GROUP OF UNITS ARE CYCLIC
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2019, pp. 403-412
-
- Article
- Export citation
ON
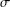 $\unicode[STIX]{x1D70E}$-QUASINORMAL SUBGROUPS OF FINITE GROUPS
$\unicode[STIX]{x1D70E}$-QUASINORMAL SUBGROUPS OF FINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 12 November 2018, pp. 413-420
-
- Article
- Export citation
NOTE ON THE CONVOLUTION OF HARMONIC MAPPINGS
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2019, pp. 421-431
-
- Article
- Export citation
GLOBAL EXISTENCE OF WEAK SOLUTIONS FOR STRONGLY DAMPED WAVE EQUATIONS WITH NONLINEAR BOUNDARY CONDITIONS AND BALANCED POTENTIALS
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2019, pp. 432-444
-
- Article
- Export citation
CONTRACTIBLE PERIODIC ORBITS OF LAGRANGIAN SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2019, pp. 445-453
-
- Article
- Export citation
DICHOTOMY PROPERTY FOR MAXIMAL OPERATORS IN A NONDOUBLING SETTING
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 454-466
-
- Article
- Export citation
DUAL DIFFERENTIATION SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2019, pp. 467-472
-
- Article
- Export citation
COMPACT WEIGHTED COMPOSITION OPERATORS ON
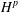 $H^{p}$-SPACES
$H^{p}$-SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2019, pp. 473-484
-
- Article
- Export citation
APPROXIMATELY ANGLE PRESERVING MAPPINGS
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2019, pp. 485-496
-
- Article
- Export citation
BEST PROXIMITY POINTS AND FIXED POINTS WITH
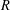 $R$-FUNCTIONS IN THE FRAMEWORK OF
$R$-FUNCTIONS IN THE FRAMEWORK OF 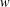 $w$-DISTANCES
$w$-DISTANCES
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2018, pp. 497-507
-
- Article
- Export citation
EMBEDDING OF METRIC GRAPHS ON HYPERBOLIC SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2019, pp. 508-520
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
THE CLASSIFICATION OF CATEGORIES GENERATED BY AN OBJECT OF SMALL DIMENSION
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 521-522
-
- Article
-
- You have access
- Export citation
A STUDY ON NUMERICAL MODELLING OF VECTOR-BORNE DISEASES
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2019, pp. 523-524
-
- Article
-
- You have access
- Export citation