No CrossRef data available.
Article contents
ON FINDING SOLUTIONS TO EXPONENTIAL CONGRUENCES
Published online by Cambridge University Press: 27 December 2018
Abstract
We improve some previously known deterministic algorithms for finding integer solutions 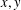 $x,y$ to the exponential equation of the form
$x,y$ to the exponential equation of the form 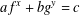 $af^{x}+bg^{y}=c$ over finite fields.
$af^{x}+bg^{y}=c$ over finite fields.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
During the preparation of this work, the author was supported in part by the Australian Research Council Grant DP170100786.


