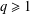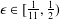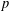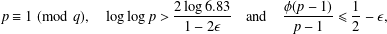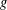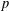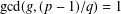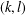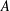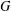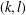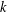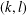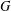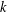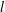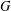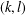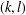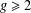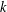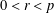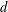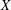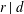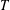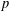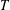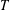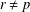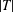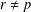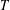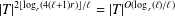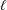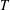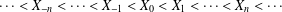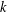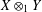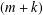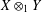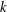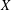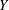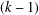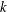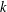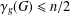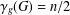Research Article
QUADRATIC NONRESIDUES AND NONPRIMITIVE ROOTS SATISFYING A COPRIMALITY CONDITION
- Part of:
-
- Published online by Cambridge University Press:
- 12 November 2018, pp. 177-183
-
- Article
-
- You have access
- Export citation
THE MAXIMUM SIZE OF
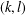 $(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
$(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 184-194
-
- Article
-
- You have access
- Export citation
ON MAXIMALLY FROBENIUS DESTABILISED VECTOR BUNDLES
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2019, pp. 195-202
-
- Article
-
- You have access
- Export citation
ON THE SECOND-LARGEST SYLOW SUBGROUP OF A FINITE SIMPLE GROUP OF LIE TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2018, pp. 203-211
-
- Article
-
- You have access
- Export citation
GROUPS SATISFYING THE DOUBLE CHAIN CONDITION ON ABELIAN SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 12 September 2018, pp. 212-218
-
- Article
-
- You have access
- Export citation
THE UNIQUE CONTINUATION PROPERTY OF
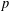 $p$-HARMONIC FUNCTIONS ON THE HEISENBERG GROUP
$p$-HARMONIC FUNCTIONS ON THE HEISENBERG GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 12 November 2018, pp. 219-230
-
- Article
-
- You have access
- Export citation
AN IMPROVED RESULT ON GROUND STATE SOLUTIONS OF QUASILINEAR SCHRÖDINGER EQUATIONS WITH SUPER-LINEAR NONLINEARITIES
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 231-241
-
- Article
-
- You have access
- Export citation
EXISTENCE AND BLOW-UP OF SOLUTIONS TO A PARABOLIC EQUATION WITH NONSTANDARD GROWTH CONDITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2018, pp. 242-249
-
- Article
-
- You have access
- Export citation
QUANTITATIVE PROPERTIES OF MEROMORPHIC SOLUTIONS TO SOME DIFFERENTIAL-DIFFERENCE EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 250-261
-
- Article
-
- You have access
- Export citation
GEOMETRIC AND FIXED POINT PROPERTIES IN PRODUCTS OF NORMED SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2019, pp. 262-273
-
- Article
-
- You have access
- Export citation
ON THE DECOMPOSITION OF OPERATORS WITH SEVERAL ALMOST-INVARIANT SUBSPACES
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2019, pp. 274-283
-
- Article
-
- You have access
- Export citation
AMENABLE SEMIGROUPS OF NONLINEAR OPERATORS IN UNIFORMLY CONVEX BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2018, pp. 284-292
-
- Article
-
- You have access
- Export citation
POSITIVE CENTRE SETS OF CONVEX CURVES AND A BONNESEN TYPE INEQUALITY
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 293-301
-
- Article
-
- You have access
- Export citation
ON GENERALISED METRISABILITY AND CARDINAL INVARIANTS IN QUASITOPOLOGICAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 17 October 2018, pp. 302-310
-
- Article
-
- You have access
- Export citation
DIFFERENTIAL FORMS ON STRATIFIED SPACES II
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2019, pp. 311-318
-
- Article
-
- You have access
- Export citation
AN EXACT ENTANGLING GATE USING FIBONACCI ANYONS
- Part of:
-
- Published online by Cambridge University Press:
- 12 November 2018, pp. 319-326
-
- Article
-
- You have access
- Export citation
THE DOMINATION GAME ON SPLIT GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 12 November 2018, pp. 327-337
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
ALGEBRAIC MODELS OF LARGE SCALE GENOME REARRANGEMENT EVENTS
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 338-339
-
- Article
-
- You have access
- Export citation
METRICS AND SPECIAL KÄHLER GEOMETRY ON THE MODULI SPACES OF HIGGS BUNDLES AND HITCHIN SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 340-341
-
- Article
-
- You have access
- Export citation
POSITIVE SCALAR CURVATURE AND CALLIAS-TYPE INDEX THEOREMS FOR PROPER ACTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 342-343
-
- Article
-
- You have access
- Export citation