Stochastic Geometry and Statistical Applications
Continuum percolation in the Gabriel graph
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 689-701
-
- Article
- Export citation
Variance prediction for pseudosystematic sampling on the sphere
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 469-483
-
- Article
- Export citation
Determining convex polygons from their covariograms
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 261-266
-
- Article
- Export citation
Limit laws for the diameter of a random point set
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2016, pp. 1-10
-
- Article
- Export citation
The set covariance of a dead leaves model
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2016, pp. 11-20
-
- Article
- Export citation
The distributions of the smallest disks containing the Poisson-Voronoi typical cell and the Crofton cell in the plane
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 702-717
-
- Article
- Export citation
Simulation of cluster point processes without edge effects
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 267-280
-
- Article
- Export citation
A note on design-based versus model-based variance estimation in stereology
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 484-490
-
- Article
- Export citation
Areas of components of a Voronoi polygon in a homogeneous Poisson process in the plane
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 281-291
-
- Article
- Export citation
Random patterns of nonoverlapping convex grains
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 718-738
-
- Article
- Export citation
A two-dimensional random crystalline algorithm for Gauss curvature flow
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 491-504
-
- Article
- Export citation
Generalized contact distributions of inhomogeneous Boolean models
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2016, pp. 21-47
-
- Article
- Export citation
The loss of tension in an infinite membrane with holes distributed according to a Poisson law
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 292-312
-
- Article
- Export citation
Critical intensities of Boolean models with different underlying convex shapes
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2016, pp. 48-57
-
- Article
- Export citation
Determination of the mean normal measure from isotropic means of flat sections
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 505-519
-
- Article
- Export citation
Focusing of the scan statistic and geometric clique number
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 739-753
-
- Article
- Export citation
General Applied Probability
Markov random field models of multicasting in tree networks
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2016, pp. 58-84
-
- Article
- Export citation
Stochastic Geometry and Statistical Applications
Variance asymptotics and central limit theorems for volumes of unions of random closed sets
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 520-539
-
- Article
- Export citation
General Applied Probability
Index policies for a class of discounted restless bandits
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 754-774
-
- Article
- Export citation
Optimal control of queueing networks: an approach via fluid models
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 313-328
-
- Article
- Export citation



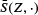 be the mean normal measure of a stationary random set
be the mean normal measure of a stationary random set 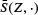 and the mean of
and the mean of 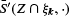 . Here, the mean is understood to be with respect to the random isotropic
. Here, the mean is understood to be with respect to the random isotropic 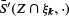 before averaging. A large class of liftings and their resulting means are discussed. In particular, a geometrically motivated lifting is presented, for which the mean of liftings of
before averaging. A large class of liftings and their resulting means are discussed. In particular, a geometrically motivated lifting is presented, for which the mean of liftings of 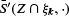 determines
determines 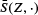 uniquely for any fixed
uniquely for any fixed