Stochastic Geometry and Statistical Applications
Random Marked Sets
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 603-616
-
- Article
-
- You have access
- Export citation
Sharpness in the k-Nearest-Neighbours Random Geometric Graph Model
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 617-634
-
- Article
-
- You have access
- Export citation
Spatial Stit Tessellations: Distributional Results for I-Segments
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 635-654
-
- Article
-
- You have access
- Export citation
General Applied Probability
Optimal Stopping Problems for Asset Management
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 655-677
-
- Article
-
- You have access
- Export citation
Nonlinear Filtering for Jump Diffusion Observations
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 678-701
-
- Article
-
- You have access
- Export citation
The Class of Tenable Zero-Balanced Pólya Urn Schemes: Characterization and Gaussian Phases
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 702-728
-
- Article
-
- You have access
- Export citation
Piecewise-Deterministic Markov Processes as Limits of Markov Jump Processes
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 729-748
-
- Article
-
- You have access
- Export citation
Averaging for a Fully Coupled Piecewise-Deterministic Markov Process in Infinite Dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 749-773
-
- Article
-
- You have access
- Export citation
The Expected Total Cost Criterion for Markov Decision Processes under Constraints: A Convex Analytic Approach
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 774-793
-
- Article
-
- You have access
- Export citation
Tail Behavior of Randomly Weighted Sums
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 794-814
-
- Article
-
- You have access
- Export citation
The Convergence Rate and Asymptotic Distribution of the Bootstrap Quantile Variance Estimator for Importance Sampling
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 815-841
-
- Article
-
- You have access
- Export citation
On Exact Sampling of Nonnegative Infinitely Divisible Random Variables
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 842-873
-
- Article
-
- You have access
- Export citation
A Simple Stochastic Kinetic Transport Model
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 874-885
-
- Article
-
- You have access
- Export citation
On the Optimal Dividend Strategy in a Regime-Switching Diffusion Model
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 886-906
-
- Article
-
- You have access
- Export citation
Front Matter
APR volume 44 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Matter
APR volume 44 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation



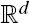 . Unlike for random fields, the mark covariance function of a random marked set is in general not positive definite. This implies that in many situations the use of simple geostatistical methods appears to be questionable. Surprisingly, for a special class of processes based on Gaussian random fields, we do have positive definiteness for the corresponding mark covariance function and mark correlation function.
. Unlike for random fields, the mark covariance function of a random marked set is in general not positive definite. This implies that in many situations the use of simple geostatistical methods appears to be questionable. Surprisingly, for a special class of processes based on Gaussian random fields, we do have positive definiteness for the corresponding mark covariance function and mark correlation function.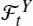 provides all the available information about
provides all the available information about 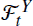 . To this end, we prove that π
. To this end, we prove that π